Study on Least Step Sequence Method for Isomorphic Identification of Kinematic Chains
-
摘要: 提出用素数刻画机构构件间的运动副,并得到运动链的素数权值矩阵。在此基础上用改进的Floyd算法得到任意两个顶点间走最少步数的最小权值连乘积矩阵,并按一定规则排序。由此映射关系反映了唯一的机构运动链的相互关系,给出两个机构运动链同构的充分必要条件,建立了运动链同构判别的新方法。该方法也适用于一般的无向图的同构判别。最后通过判别实例表明该方法准确、简单且易于在计算机实现,同构判别的解决为机构综合与分析奠定了基础。Abstract: It is proposed to use the prime number to describe the motion pair between the components of the mechanism and obtain the matrix of prime weights of the kinematic chain. Based on this, the improved Floyd algorithm is used to obtain the minimum weight continuous product matrix with the least number of steps between any two vertices, and sorted according to certain rules. The mapping relationship reflects the mutual relationship of the unique institutional kinematic chain, and gives the necessary and sufficient conditions for the isomorphism of the two institutions' kinematic chains. A new method for the isomorphism identification of kinematic chains is established. This method is also applicable to the isomorphic discrimination of general undirected graphs. Finally, the discriminated examples show that the method is accurate, simple and easy to implement in computer. The solution of isomorphic discrimination lays the foundation for institutional synthesis and analysis.
-
Key words:
- prime weights matrix /
- Floyd algorithm /
- kinematic chain /
- isomorphism identification
-
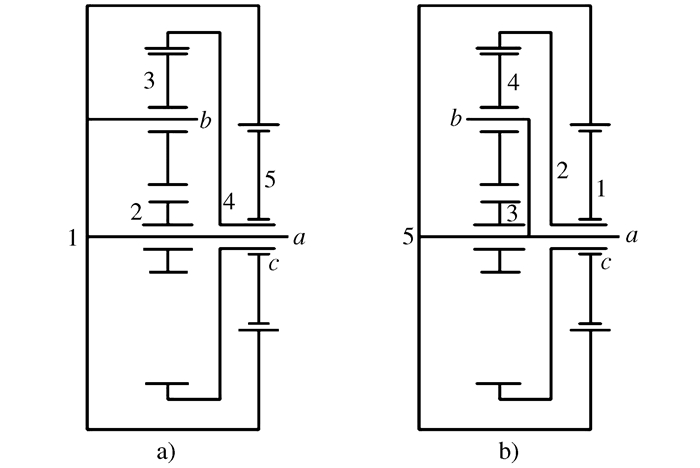
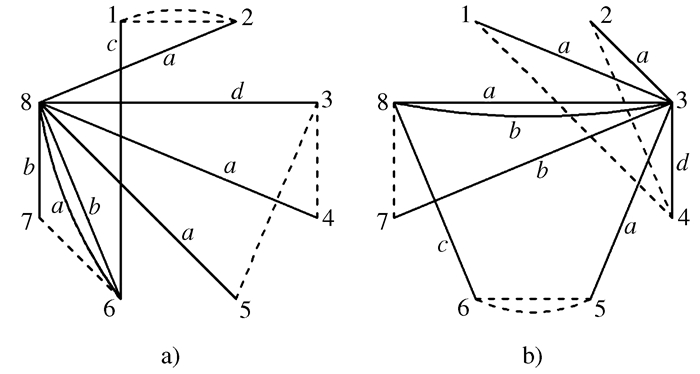
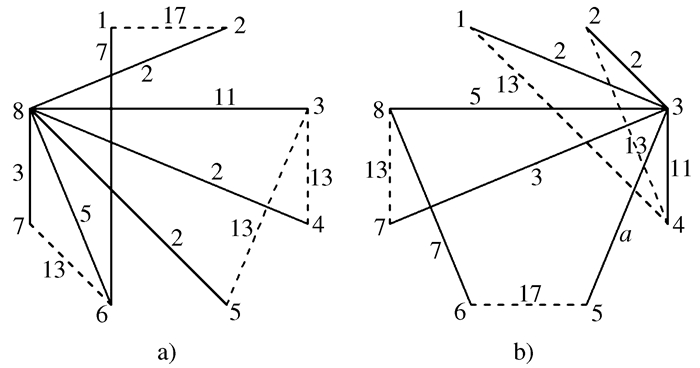
表 1 六轮轮系素数权值分配
a边 b边 重实边 c边 d边 虚边 重虚边 2 3 5 7 11 13 17 -
[1] Ding H F, Huang Z. A new theory for the topological structure analysis of kinematic chains and its applications[J]. Mechanism and Machine Theory, 2007, 42(10):1264-1279 doi: 10.1016/j.mechmachtheory.2006.11.007 [2] 伍星华, 聂松辉.平面运动链同构识别的全等环路法[J].机械科学与技术, 2009, 28(2):205-209 doi: 10.3321/j.issn:1003-8728.2009.02.015Wu X H, Nie S H. Congruent loop approach to isomorphism identification of planar kinematic chains[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(2):205-209(in Chinese) doi: 10.3321/j.issn:1003-8728.2009.02.015 [3] 伍星华, 聂松辉, 李宁波.平面运动链简图自动绘制的初始回路法[J].机械科学与技术, 2009, 28(4):546-552 doi: 10.3321/j.issn:1003-8728.2009.04.028Wu X H, Nie S H. Li L B. An Approach of original loop to automatic sketching of planar kinematic chains[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(4):546-552(in Chinese) doi: 10.3321/j.issn:1003-8728.2009.04.028 [4] 王英.运动链型综合的基本回路方法及混合驱动机构构型设计[D].太原: 中北大学, 2016Wang Y. Basic loop method on type synthesis of kinematic chain and configuration design of hybrid driven mechanism[D]. Taiyuan: North University of China, 2016(in Chinese) [5] Cubillo J P, Wan J B. Comments on mechanism kinematic chain isomorphism identification using adjacent matrices[J]. Mechanism and Machine Theory, 2005, 40(2):131-139 doi: 10.1016/j.mechmachtheory.2004.07.004 [6] He P R, Zhang W J, Li Q, et al. A new method for detection of graph isomorphism based on the quadratic form[J]. Journal of Mechanical Design, 2003, 125(3):640-642 doi: 10.1115/1.1564574 [7] Yan H S, Hall A S. Linkage characteristic polynomials: definitions, coefficients by inspection[J]. Journal of Mechanical Design, 1981, 103(3):578-584 doi: 10.1115/1.3254957 [8] Uicker Jr J J, Raicu A. A method for the identification and recognition of equivalence of kinematic chains[J]. Mechanism and Machine Theory, 1975, 10(5):375-383 doi: 10.1016/0094-114X(75)90037-3 [9] Mruthyunjaya T S, Balasubramanian H R. In quest of a reliable and efficient computational test for detection of isomorphism in kinematic chains[J]. Mechanism and Machine Theory, 1987, 22(2):131-139 doi: 10.1016/0094-114X(87)90036-X [10] Ambekar A G, Agrawal V P. Canonical numbering of kinematic chains and isomorphism problem: min code[J]. Mechanism and Machine Theory, 1987, 22(5):453-461 doi: 10.1016/0094-114X(87)90062-0 [11] Tang C S, Liu T. The degree code-a new mechanism identifier[J]. Journal of Mechanical Design, 1993, 115(3):627-630 doi: 10.1115/1.2919236 [12] Fang W E, Freudenstein F. The stratified representation of mechanisms[J]. Journal of Mechanical Design, 1990, 112(4):514-519 doi: 10.1115/1.2912640 [13] Shin J K, Krishnamurty S. Development of a standard code for colored graphs and its application to kinematic chains[J]. Journal of Mechanical Design, 1994, 116(1): 189-196 doi: 10.1115/1.2919345 [14] 丁华锋, 黄真.平面机构统一拓扑描述模型的建立及同构判别[J].机械工程学报, 2009, 45(3):99-103 http://d.old.wanfangdata.com.cn/Periodical/jxgcxb200903014Ding H F, Huang Z. Uniform topological representation model of planar mechanisms and isomorphism identification[J]. Journal of Mechanical Engineering, 2009, 45(3):99-103(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxgcxb200903014 [15] Barrus M D. On 2-switches and isomorphism classes[J]. Discrete Mathematics, 2012, 312(15):2217-2222 doi: 10.1016/j.disc.2012.04.014 [16] 张清华, 陈六新, 李永红.图论及其应用[M].北京:清华大学出版社, 2013:40-95Zhang Q H, Chen L X, Li Y H. Graph theory with applications[M]. Beijing: Tsinghua University Press, 2013:40-95(in Chinese) [17] 丁玲, 路懿.运动链拓扑图的特征数组表示及同构判断[J].机械工程学报, 2010, 46(7):63-67 http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201007010Ding L, Lu Y. Character arrays representation and isomorphism identification of kinematic chain topology graphs[J]. Journal of Mechanical Engineering, 2010, 46(7):63-67(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201007010 -








 下载:
下载: