圆度误差的神经网络评定及测量不确定度研究

张珂; 张玮; 阎卫增; 侯怀书

doi:10.13433/j.cnki.1003-8728.20180324

圆度误差的神经网络评定及测量不确定度研究

doi: 10.13433/j.cnki.1003-8728.20180324

1.
上海应用技术大学机械工程学院, 上海 201418
2.
上海思博特轴承技术研发有限公司, 上海 201400

基金项目:

上海市联盟计划项目 LM201635

上海应用技术大学协同创新基金项目 XTCX2018-13

详细信息

作者简介:
张珂(1968-), 教授, 博士, 研究方向为机械设计、机械精密测量, zkwy2004@126.com

中图分类号: TH161
计量
- 文章访问数: 157
- HTML全文浏览量: 78
- PDF下载量: 29
- 被引次数: 0
出版历程
- 收稿日期: 2018-05-02
- 刊出日期: 2019-03-05

Research on Evaluation and Uncertainty of Measurement of Circularity Errors via Neural Network Algorithm

1.
School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 201418, China
2.
Shanghai Sibote Bearing Technology Development Co., Ltd., Shanghai 201400, China

摘要

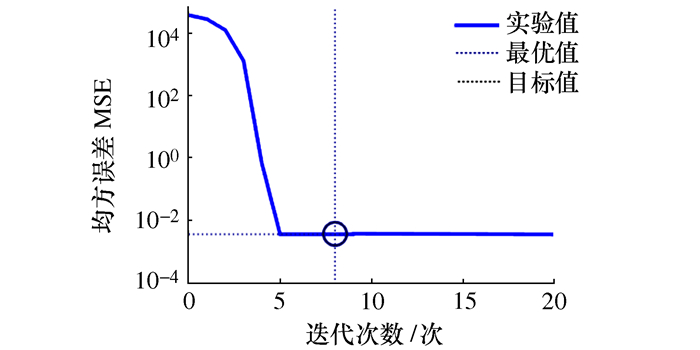
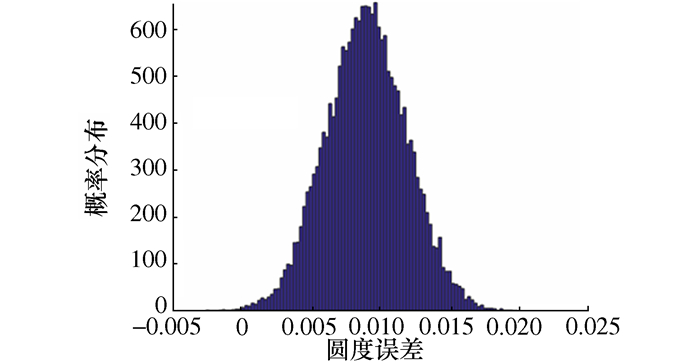
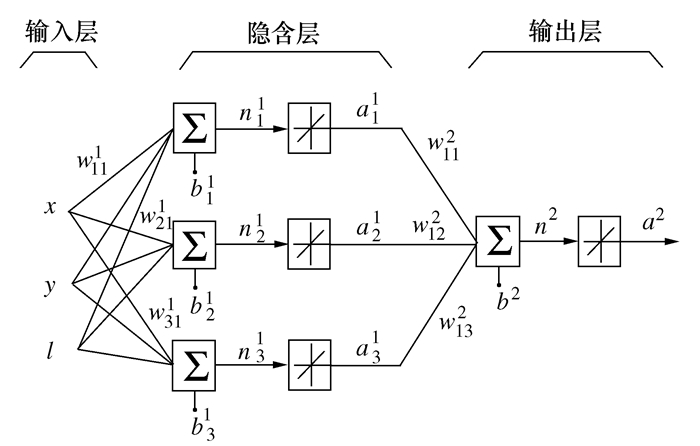
摘要: 为了更为准确的而又简便的评定圆度误差及其不确定度，根据最小二乘法建立圆度误差模型，基于BP神经网络算法优化目标函数的参数，阐述了BP神经网络优化算法的原理和实现方法。通过求解实例表明该方法对于圆度误差评定的非线性优化问题能得到最优解。采用传统的测量不确定度表示指南方法和蒙特卡洛方法计算得到圆度误差的不确定度，通过实例验证蒙特卡洛法的可靠性和准确性。该方法不需要求出数学模型中的传递系数，利用MATLAB操作简单，为圆度误差测量结果不确定度评定提供了更加简便的方法。
- BP神经网络 /
- 圆度误差 /
- 不确定度 /
- 蒙特卡洛法 /
Abstract: In order to evaluate the circularity errors and its uncertainty more accurately and easily, the circularity error model is established with the least square method, and the parameters of objective function are optimized via BP neural network algorithm. The principle and implementation method of BP neural network algorithm are described. An example is given to show that the method can obtain the optimal solution for the nonlinear optimization problem of circularity errors evaluation. The uncertainty of roundness error is calculated with the Guide to expression of uncertainty in measurement (GUM) and Monte Carlo method. The reliability and accuracy of Monte Carlo method are verified. This method does not need to calculate the transfer coefficient of the model. It is easy to realize via MATLAB and provides a more convenient method for evaluating uncertainty of circularity error measurement results.
- BP neural network /
- circularity errors /
- uncertainty /
- Monte Carlo method /
- MATLAB

HTML全文

图 1 神经网络的结构图

下载: 全尺寸图片幻灯片

图 2 迭代次数与圆度误差均方差值之间的曲线关系

下载: 全尺寸图片幻灯片

图 3 圆度误差的概率分布直方图

下载: 全尺寸图片幻灯片

表 1 圆柱截面测点坐标值

mm
序号	x	y
1	8.357 2	-11.300 8
2	6.279 5	-12.588 6
3	4.005 6	-13.495 8
4	1.621 9	-13.993 3
5	-0.815 7	-14.070 6
6	-3.228 0	-13.725 0
7	-5.539 2	-12.959 8
8	-7.695 2	-11.807 3
9	-9.607 6	-10.303 5
10	-11.253 2	-8.466 8
11	-12.556 8	-6.342 5
12	-13.455 8	-4.069 1
13	-13.948 4	-1.729 3
14	-14.021 8	0.722 4
15	-13.679 1	3.121 1
16	-12.906 4	5.456 1
17	-11.748 9	7.608 1
18	-10.225 1	9.544 7
19	5.480 4	12.804 4
20	7.633 2	11.654 3
21	9.554 3	10.145 4
22	11.189 0	8.311 7
23	12.470 5	6.246 0
24	13.381 5	3.955 6
25	13.873 3	1.588 4
26	13.950 9	-0.866 3
27	13.601 4	-3.279 3
28	12.857 2	-5.552 6
29	11.704 2	-7.719 1
30	10.176 1	-9.674 5
31	-8.403 1	11.160 5
32	-6.322 8	12.443 3
33	-4.070 1	13.340 1
34	-1.681 6	13.835 2
35	0.759 9	13.911 7
36	3.167 2	13.565 3

下载: 导出CSV

表 2 各种圆度误差评定算法计算结果对比

mm
参数	最小二乘法	改进遗传算法^[14]	BP神经网络算法
A	-	-	-0.066 08
B	-	-	-0.154 96
C	-	-	196.338 8
误差	0.009 871	0.009 1	0.008 879

下载: 导出CSV

表 3 不同方法评定测量不确定度结果对比

mm
方法	BP神经网络	最小二乘法
GUM法	0.003 091	0.002 906
蒙特卡洛法	0.002 903	0.002 913

下载: 导出CSV

参考文献(16)

[1]	Srinivasu D S, Venkaiah N. Minimum zone evaluation of roundness using hybrid global search approach[J]. International Journal of Advanced Manufacturing Technology, 2017, 92(5-8):2743-2754 doi: 10.1007/s00170-017-0325-y
[2]	胡仲勋, 董青林, 刘子建.三维空间中圆度误差的评定研究[J].机械科学与技术, 2013, 32(10):1422-1427 http://journals.nwpu.edu.cn/jxkxyjs/CN/abstract/abstract5128.shtml Hu Z X, Dong Q L, Liu Z J. Study on the evaluation methods of circularity errors in three-dimensional space[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(10):1422-1427(in Chinese) http://journals.nwpu.edu.cn/jxkxyjs/CN/abstract/abstract5128.shtml
[3]	丁玲.圆度与圆柱度误差评定算法的设计与应用[D].西安: 西安电子科技大学, 2013 Ding L. Design and application of roundness and cylindricity error evaluation algorithms[D]. Xi'an: Xidian University, 2013(in Chinese)
[4]	Cui C C, Li B, Huang F G, et al. Genetic algorithm-based from error evaluation[J]. Measurement Science and Technology, 2007, 18(7):1818-1822 doi: 10.1088/0957-0233/18/7/004
[5]	Zhang K, Kong X S, Luo J P, et al. Study on straightness error evaluation of spatial lines based on a hybrid ant colony algorithm[J]. International Journal of Wireless and Mobile Computing, 2015, 8(3):277-284 doi: 10.1504/IJWMC.2015.069390
[6]	张玉梅, 左春柽, 刘岩, 等.基于人工免疫算法的轴线直线度误差评定[J].计量学报, 2010, 31(6):490-493 http://d.old.wanfangdata.com.cn/Periodical/jlxb98201006003 Zhang Y M, Zuo C C, Liu Y, et al. Evaluation method for axis straightness error based on artificial immune optimization algorithm[J]. Acta Metrologica Sinica, 2010, 31(6):490-493(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jlxb98201006003
[7]	Zhang K, Luo J P. Research on flatness errors evaluation based on artificial fish swarm algorithm and powell method[J]. International Journal of Computing Science and Mathematics, 2013, 4(4):402-411 doi: 10.1504/IJCSM.2013.058060
[8]	葛动元, 姚锡凡, 向文江.BP神经网络在麻花钻圆度误差检测中的应用研究[J].武汉科技大学学报, 2009, 32(4):413-417 doi: 10.3969/j.issn.1674-3644.2009.04.017 Ge D Y, Yao X F, Xiang W J. Application of BP neural network for measurement of twist-drill circularity errors[J]. Journal of Wuhan University of Science and Technology, 2009, 32(4):413-417(in Chinese) doi: 10.3969/j.issn.1674-3644.2009.04.017
[9]	王汉斌, 陈晓怀, 程银宝, 等.基于新一代GPS的产品检验符合性不确定度评定[J].机械工程学报, 2016, 52(24):194-200 http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201624024 Wang H B, Chen X H, Cheng Y B, et al. Evaluation of compliance uncertainty in product inspection based on the new generation geometrical product specifications[J]. Journal of Mechanical Engineering, 2016, 52(24):194-200(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201624024
[10]	吴呼玲.基于MATLAB的直线度测量不确定度评定程序设计[J].计算机测量与控制, 2017, 25(12):288-290 http://d.old.wanfangdata.com.cn/Periodical/jsjzdclykz201712074 Wu H L. Program design of linear measurement uncertainty evaluation based on MATLAB[J]. Computer Measurement & Control, 2017, 25(12):288-290(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jsjzdclykz201712074
[11]	吴呼玲.基于蒙特卡罗法与GUM法的直线度测量不确定度评定[J].工具技术, 2017, 51(5):104-107 doi: 10.3969/j.issn.1000-7008.2017.05.026 Wu H L. Straightness measurement uncertainty evaluation based on Monte Carlo method and GUM method[J]. Tool Engineering, 2017, 51(5):104-107(in Chinese) doi: 10.3969/j.issn.1000-7008.2017.05.026
[12]	张德丰.MATLAB神经网络编程[M].北京:化学工业出版社, 2011 Zhang D F. MATLAB neural network programming[M]. Beijing:Chemical Industry Press, 2011(in Chinese)
[13]	周菁菁.一种BP神经网络的改进算法及其应用[D].兰州: 兰州大学, 2017 http://www.cnki.com.cn/Article/CJFDTotal-GCKX200505010.htm Zhou J J. An improved BP neural network algorithm and its application[D]. Lanzhou: Lanzhou University, 2017(in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-GCKX200505010.htm
[14]	潘俊, 温秀兰.圆度误差评定与测量不确定度计算[J].南京工程学院学报:自然科学版, 2015, 13(1):1-5 http://d.old.wanfangdata.com.cn/Periodical/njgcxyxb-zrkxb201501001 Pan J, Wen X L. Evaluation of circularity errors and computation of measurement uncertainty[J]. Journal of Nanjing Institute of Technology:Natural Science Edition, 2015, 13(1):1-5(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/njgcxyxb-zrkxb201501001
[15]	连慧芳.形位误差测量的不确定度评定[D].合肥: 合肥工业大学, 2010 http://cdmd.cnki.com.cn/Article/CDMD-10359-2010246755.htm Lian H F. Evaluation of measurement uncertainty in result of form and position error[D].Hefei: Heifei University of Techology, 2010(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10359-2010246755.htm
[16]	刘存成, 胡畅.基于MATLAB用蒙特卡洛法评定测量不确定度[M].北京:中国质检出版社, 2014 Liu C H, Hu C. Evaluation of uncertainty in measurement using Monte Carlo method based on Matlab[M].Beijing:Zhijian Publishing House, 2014(in Chinese)