A Solving Method for Inverse Kinematics of Space 3R Manipulator based on Singular Trajectory Theory
-
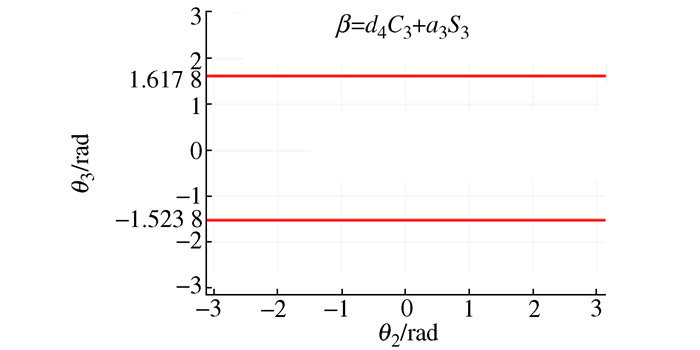
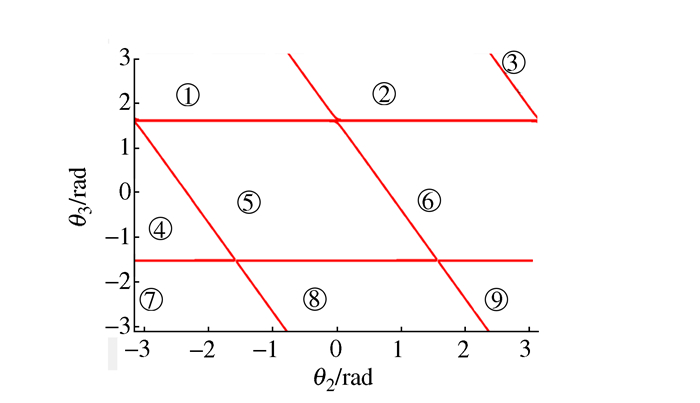
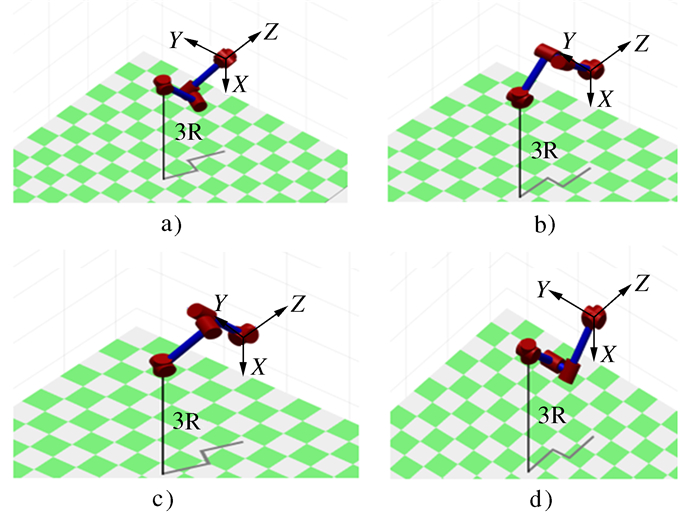
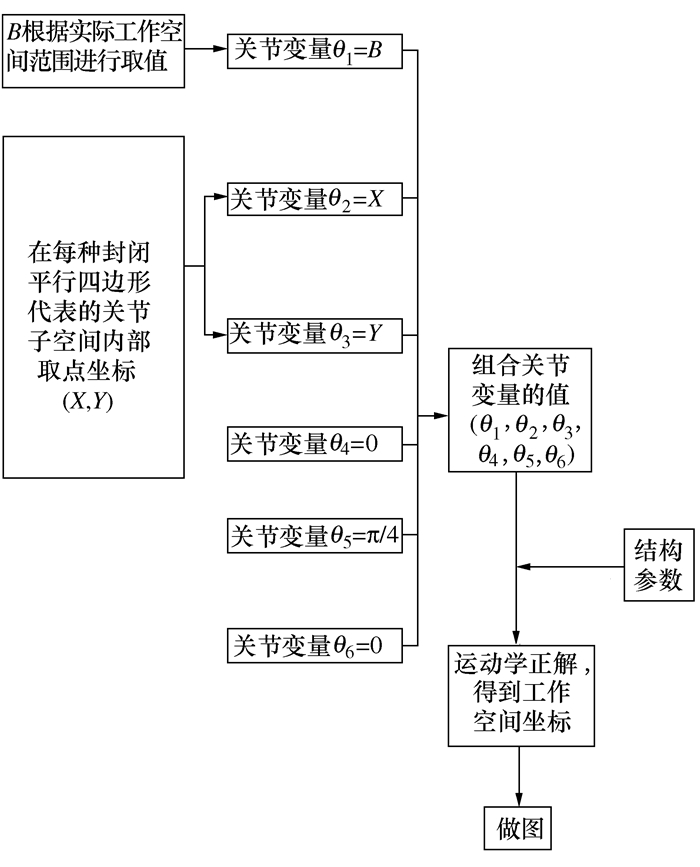
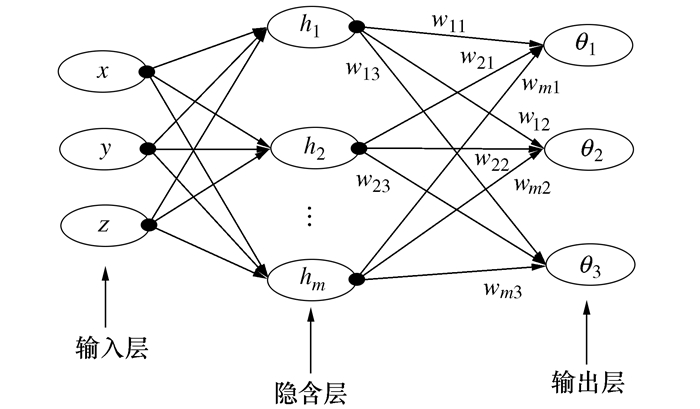
摘要: 针对机器人逆运动学多解问题,提出一种基于奇异轨迹线的多模块径向基神经网络的求解方法。根据奇异轨迹线理论,将关节空间严格划分成只具有单逆解的多个关节子空间区域,然后通过正向运动学,使各个关节子空间映射到同一工作空间,以获得多组工作空间位置相同但是关节区域不同的训练样本,每组训练样本只含单逆解。在多模块径向基神经网络结构中,每个子模块分别负责学习一组训练样本,从而将逆运动学多解求取问题转化为各个子模块对神经网络权值的训练问题,通过神经网络结构中的多个模块逆解预测,实现了机器人逆运动学的多解计算。算例表明基于奇异轨迹线的多模块神经网络能够正确输出多组逆解,满足求解精度要求,在逆运动学多解求取中具有较好的推广价值。Abstract: Aiming at the multi-solution problem of robot inverse kinematics, a solution method of multi-module radial basis function network based on singular trajectory is proposed. According to the singular trajectory theory, the joint space is strictly divided into multiple joint subspace regions with only single inverse solution. Then, through forward kinematics, each joint subspace is mapped to the same workspace to obtain multiple sets of training samples with the same working space but different joint regions. Each training sample only contains a single inverse solution. In a multi-module radial basis neural function network structure, each sub-module is responsible for learning a set of training samples. Therefore, the inverse kinematics multiple solution problem is transformed into the training problem of neural network weights of each sub-module. Multi-solution calculation of robot inverse kinematics is realized by inverse solution prediction of multiple modules in neural network structure. The example shows that multi-module neural networks based on singular trajectories can correctly output multiple sets of inverse solutions, moreover, it satisfies the requirements of solving accuracy and has a good generalization value in the inverse kinematics solution.
-
Key words:
- robots /
- singular trajector /
- multitasking /
- radial basis function networks
-
表 1 6自由度机器人的DH参数
关节转角
θi/(°)连杆距离
di/m连杆长度
ai/m连杆扭角
αi/(°)θ1 0 0 90 θ2 0 0.431 8 0 θ3 0.15 0.020 3 -90 θ4 0.431 8 0 90 θ5 0 0 -90 θ6 0 0 0 表 2 基于奇异的轨迹的逆解种类分布
表 3 两个随机点的多模块神经网络逆解及误差
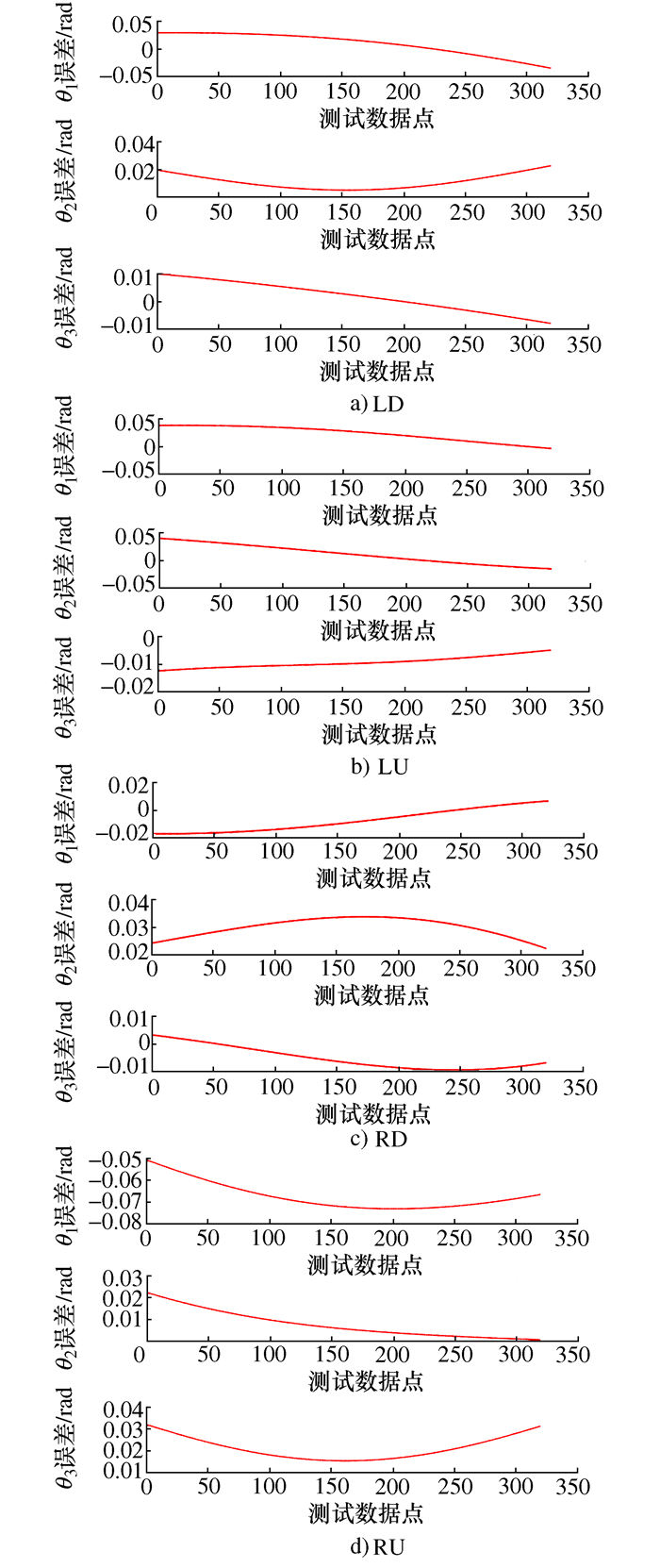
空间位置点 (0.22, 0.27, 0.14) (0.36, 0.40, 0.42) LD RBF逆解 (3.592, 3.867, 2.372) (3.651, 3.130, 3.351) 位置 (0.191, 0.259, 0.144) (0.361, 0.373, 0.432) 绝对误差E (0.029, 0.012, 0.004) (0.001, 0.027, 0.012) LU RBF逆解 (3.575, 1.656, 0.822) (3.633, 1.699, -0.111) 位置 (0.226, 0.270, 0.103) (0.359, 0.362, 0.441) 绝对误差E (0.006, 0.000, 0.037) (0.001, 0.038, 0.021) RD RBF逆解 (1.341, -0.857, 0.873) (1.150, 0.066, -0.355) 位置 (0.213, 0.254, 0.106) (0.372, 0.462, 0.437) 绝对误差E (0.007, 0.016, 0.034) (0.012, 0.062, 0.017) RU RBF逆解 (1.412, 1.653, 2.424) (1.088, 1.352, 3.335) 位置 (0.196, 0.273, 0.158) (0.376, 0.395, 0.390) 绝对误差E (0.025, 0.003, 0.018) (0.016, 0.005, 0.030) 表 4 多模块神经网络4组预测逆解平均绝对误差
位型逆解 θe1 θe2 θe3 RU 0.067 7 0.007 6 0.021 3 RD 0.009 1 0.030 5 0.006 0 LU 0.026 0 0.016 9 0.009 2 LD 0.019 3 0.011 0 0.004 7 -
[1] 蔡自兴.机器人学[M].北京:清华大学出版社, 2000Cai Z X. Robotics[M]. Beijing:Tsinghua University Press, 2000(in Chinese) [2] 张义.径向基函数神经网络的优化研究[D].山东淄博: 山东理工大学, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10433-1016230902.htmZhang Y. Optimization of the RBF neural network[D]. Shandong Zibo: Shandong University of Technology, 2016(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10433-1016230902.htm [3] 张培艳, 吕恬生, 宋立博.基于径向基函数网络的MOTOMAN机械手运动学逆解[J].机械科学与技术, 2004, 23(5):523-525 doi: 10.3321/j.issn:1003-8728.2004.05.007Zhang P Y, Lü T S, Song L B. A RBF-Network-Based method for solving inverse kinematics of MOTOMAN manipulator[J]. Mechanical Science and Technology, 2004, 23(5):523-525(in Chinese) doi: 10.3321/j.issn:1003-8728.2004.05.007 [4] 韩兴国, 殷鸣, 刘晓刚, 等.6R机器人逆运动学求解与运动轨迹仿真[J].四川大学学报:工程科学版, 2015, 47(6):185-190 http://d.old.wanfangdata.com.cn/Periodical/scdxxb-gckx201506026Han X G, Yin M, Liu X G, et al. Solution of inverse kinematics and movement trajectory simulation for 6R robot[J]. Journal of Sichuan University:Engineering Science Edition, 2015, 47(6):185-190(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/scdxxb-gckx201506026 [5] 卢香利, 王弦, 鲍务均, 等.巡线机器人运动学模型的建立及正逆解的求取[J].机械研究与应用, 2011(3):41-43 doi: 10.3969/j.issn.1007-4414.2011.03.013Lu X L, Wang X, Bao W J, et al. The establishment of kinematics model of inspection robot and study on solving the inverse solution of the kinematics equation[J]. Mechanical research & Application, 2011(3):41-43(in Chinese) doi: 10.3969/j.issn.1007-4414.2011.03.013 [6] Wenger P. Uniqueness Domains and Regions of feasible paths for cuspidal manipulators[J]. IEEE Transactions on Robotics, 2004, 20(4):745-750 doi: 10.1109/TRO.2004.829467 [7] Elgazzar S. Efficient kinematic transformations for the PUMA 560 robot[J]. IEEE Journal on Robotics and Automation, 1985, 1(3):142-151 doi: 10.1109/JRA.1985.1087013 [8] Moulianitis V C, Kokkinopoulos E M, Aspragathos N A. A method for the approximation of the multiple IK solutions of regular manipulators based on the uniqueness domains and using MLP[M]//Zeghloul S, Laribi M A, Gazeau J P. Robotics and Mechatronics. Cham: Springer, 2016: 273-281 [9] 王伟, 谢明红, 周国义.6-DOF工业机器人逆解优化及其工作空间的研究[J].机械与电子, 2011(1):57-60 doi: 10.3969/j.issn.1001-2257.2011.01.017Wang W, Xie M H, Zhou G Y. Research on kinematic inverse optimization and its working space of 6-DOF industry robot[J]. Machinery & Electronics, 2011(1):57-60(in Chinese) doi: 10.3969/j.issn.1001-2257.2011.01.017 [10] 韩蔚.RBF神经网络与多层感知器区分与替代问题的研究[J].科技创新导报, 2011(28):1 doi: 10.3969/j.issn.1674-098X.2011.28.001Han W. Research on RBF neural network and multilayer perceptron distinguish from substitution problem[J]. Science and Technology Consulting Herald, 2011(28):1(in Chinese) doi: 10.3969/j.issn.1674-098X.2011.28.001 [11] 于凌涛, 王文杰, 王正雨, 等.一类不满足Pieper准则的机器人逆运动学解析解获取方法[J].机器人, 2016, 38(4):486-494 http://d.old.wanfangdata.com.cn/Periodical/jqr201604013Yu L T, Wang W J, Wang Z Y, et al. Acquisition method of inverse kinematics analytical solutions for a class of robots dissatisfying the Pieper criterion[J]. Robot, 2016, 38(4):486-494(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jqr201604013 [12] 机器人学、机器视觉与控制[M].刘荣, 译.北京: 电子工业出版社, 2016Corke P. Robotics, vision and control[M]. Liu R, trans. Beijing: Publishing House of Electronics Industry, 2016(in Chinese) [13] Wenger P. Cuspidal and noncuspidal robot manipulators[J]. Robotica, 2007, 25(6):667-689 http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0213769068/ [14] 孙树栋.工业机器人技术基础[M].西安:西北工业大学出版社, 2006Sun S D. Fundamentals of robotics[M]. Xi'an:Northwestern Polytechnical University Press, 2006(in Chinese) [15] 李宪华, 盛蕊, 张雷刚, 等.六自由度模块化机器人手臂奇异构型分析[J].农业机械学报, 2017, 48(7):376-382 http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201707048Li X H, Sheng R, Zhang L G, et al. Singular configuration analysis of 6-DOF modular manipulator[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(7):376-382(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201707048 [16] Cheng F T, Hour T L, Sun Y Y, et al. Study and resolution of singularities for a 6-DOF PUMA manipulator[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 1997, 27(2):332-343 doi: 10.1109/3477.558842 [17] 陈明.MATLAB神经网络原理与实例精解[M].北京:清华大学出版社, 2013Chen M. MATLAB neural network principle and case analysis[M]. Beijing:Tsinghua University Press, 2013(in Chinese) [18] 刘金琨.机器人控制系统的设计与MATLAB仿真[M].北京:清华大学出版社, 2008Liu J K. Design of robot control system and MATLAB simulation[M]. Beijing:Tsinghua University Press, 2008(in Chinese) -








 下载:
下载: