Research on Adaptive Layering Algorithm of Triangular Facet Normal Vector of STL Model in Additive Manufacturing
-
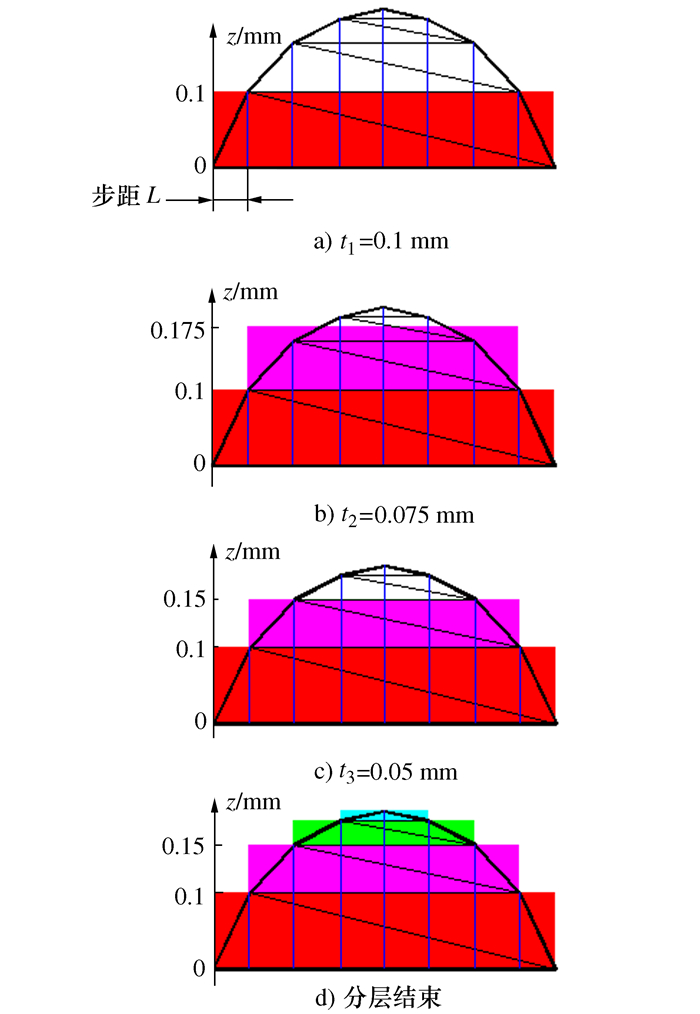
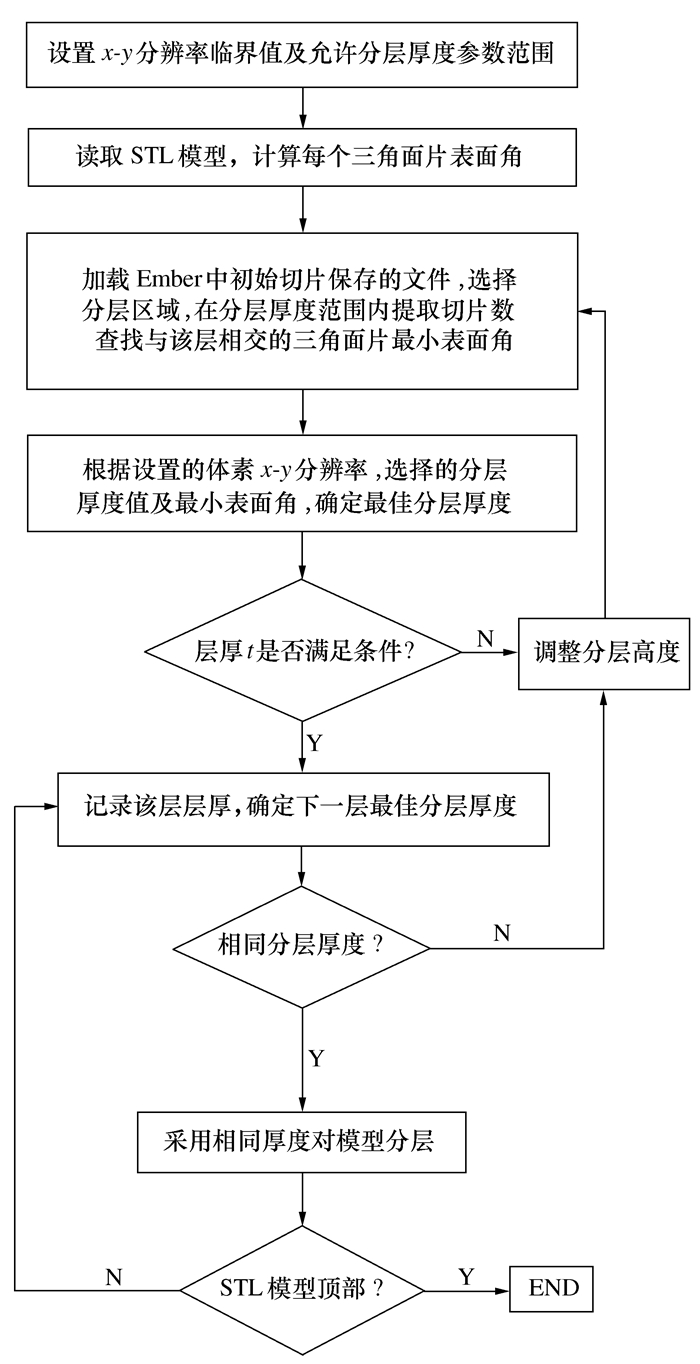
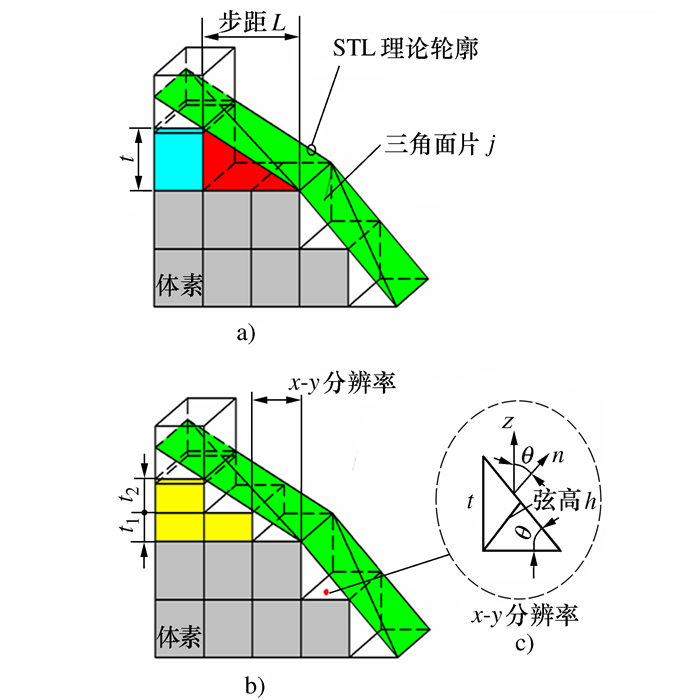
摘要: 本文提出了增材制造技术中STL模型三角面片法向量自适应分层新算法。该方法寻找与层厚t相交的三角面片的最小法向量,应用三维模型体素中x-y分辨率和STL模型中三角面片法向量与制造方向间夹角变化关系,实现STL模型的自适应分层。用此方法分层,减少了分层参数处理的复杂性,使自适应分层变得更加简单且易实现,得到的分层厚度值更加准确。由于自适应分层是在允许的误差范围内得到的分层厚度,因此在STL模型轮廓变化明显的区域分层更加精细。Abstract: In the paper, a new algorithm for the adaptive layering of triangular facet of the stereolithography(STL) model is proposed in the additive manufacturing technology. In this method, the minimum normal vector of the triangular facet intersecting with the thickness t of the layer is found, and then the relationship between the x-y resolution in the three-dimensional model voxels and the triangular facet normal vector in the STL model and the change direction of the manufacturing direction is applied to achieve adaptive layer of the STL model. With this method, the complexity of layering parameter processing is reduced, the adaptive layering becomes simpler and easier to realize, and the obtained layer thickness is more accurate. Since the adaptive layering is the layer thickness obtained within the allowable errors range, layering in the contour change area of the STL model is more refined.
-
Key words:
- additive manufacturing /
- STL model /
- adaptive layering /
- triangular facet /
- normal vector
-
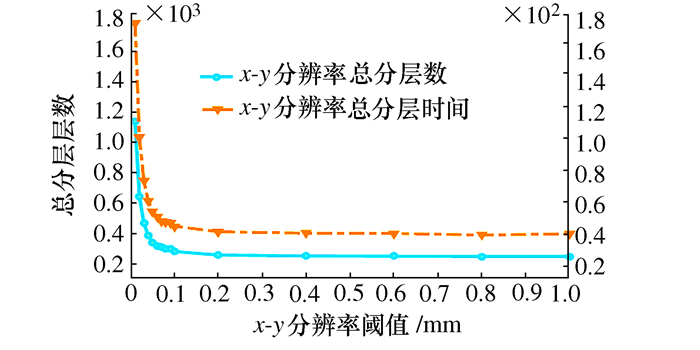
图 6 表 2中自适应分层总分层数、总生成分层数时间与x-y分辨率关系曲线
表 1 不同表面角对应的分层厚度
最小表面角θ/(°) 分层厚度/mm x-y分辨率0.01 mm x-y分辨率0.05 mm x-y分辨率0.1 mm 5 0.01 0.01 0.01 10 0.01 0.01 0.015 15 0.01 0.01 0.025 20 0.01 0.015 0.035 25 0.01 0.02 0.045 30 0.01 0.025 0.055 35 0.01 0.035 0.07 40 0.01 0.04 0.08 45 0.01 0.05 0.1 50 0.01 0.055 0.1 55 0.01 0.07 0.1 60 0.015 0.085 0.1 65 0.02 0.1 0.1 70 0.025 0.1 0.1 75 0.035 0.1 0.1 80 0.055 0.1 0.1 85 0.1 0.1 0.1 90 0.1 0.1 0.1 95 0.1 0.1 0.1 100 0.055 0.1 0.1 105 0.035 0.1 0.1 110 0.025 0.1 0.1 115 0.02 0.1 0.1 120 0.015 0.085 0.1 125 0.01 0.07 0.1 130 0.01 0.055 0.1 135 0.01 0.05 0.1 140 0.01 0.04 0.08 145 0.01 0.035 0.07 150 0.01 0.025 0.055 155 0.01 0.02 0.045 160 0.01 0.015 0.035 165 0.01 0.01 0.025 170 0.01 0.01 0.015 175 0.01 0.01 0.01 180 0.01 0.01 0.01 表 2 不同x-y分辨率的自适应分层的分层数和分层耗时比较
x-y分辨率/mm 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.2 0.4 0.6 0.8 1 分层总数 1138 646 471 387 343 320 310 303 298 259 253 251 250 250 分层耗时/s 178.815 103.289 74.935 61.621 54.456 51.192 48.091 47.774 46.824 41.236 40.284 40.106 39.106 39.791 -
[1] 罗楠, 王泉, 刘红霞.一种快速3D打印分层方向确定算法[J].西安交通大学学报, 2015, 49(5):140-146 http://d.old.wanfangdata.com.cn/Periodical/xajtdxxb201505022Luo N, Wang Q, Liu H X. A fast determination algorithm for slicing direction of 3D printing[J]. Journal of Xi'an Jiaotong University, 2015, 49(5):140-146(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/xajtdxxb201505022 [2] Sikder S, Barari A, Kishawy H A. Global adaptive slicing of NURBS based sculptured surface for minimum texture error in rapid prototyping[J]. Rapid Prototyping Journal, 2015, 21(6):649-661 doi: 10.1108/RPJ-09-2013-0090 [3] Taufik M, Jain P K. Laser assisted finishing process for improved surface finish of fused deposition modelled parts[J]. Journal of Manufacturing Processes, 2017, 30:161-177 doi: 10.1016/j.jmapro.2017.09.020 [4] 龚运息, 陈晨, 夏名祥, 等.FDM 3D打印模型表面阶梯效应的分析[J].制造技术与机床, 2016(4):27-30 doi: 10.3969/j.issn.1005-2402.2016.04.010Gong Y X, Chen C, Xia M X, et al. Step effect analysis of FDM 3D printing model surface[J]. Manufacturing Technology & Machine Tool, 2016(4):27-30(in Chinese) doi: 10.3969/j.issn.1005-2402.2016.04.010 [5] Minetto R, Volpato N, Stolfi J, et al. An optimal algorithm for 3D triangle mesh slicing[J]. Computer-Aided Design, 2017, 92:1-10 doi: 10.1016/j.cad.2017.07.001 [6] 陈昆, 潘小帝, 陈定方.一种快速成型自适应分层算法[J].武汉理工大学学报:交通科学与工程版, 2014, 38(3):547-551 http://d.old.wanfangdata.com.cn/Periodical/whjtkjdxxb201403017Chen K, Pan X D, Chen D F. An adaptive slicing algorithm of rapid prototyping[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering, 2014, 38(3):547-551(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/whjtkjdxxb201403017 [7] 郑华林, 王浩宇.快速成型中有效保留模型特征的自适应分层方法[J].应用光学, 2017, 38(5):758-763 http://d.old.wanfangdata.com.cn/Periodical/yygx201705013Zheng H L, Wang H Y. Adaptive slicing algorithm to keep model characteristics for rapid prototyping[J]. Journal of Applied Optics, 2017, 38(5):758-763(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/yygx201705013 [8] Luo N, Wang Q. Fast slicing orientation determining and optimizing algorithm for least volumetric error in rapid prototyping[J]. The International Journal of Advanced Manufacturing Technology, 2016, 83(5-8):1297-1313 doi: 10.1007/s00170-015-7571-7 [9] 周惠群, 吴建军.基于STL模型的轮廓线自适应分层方法研究[J].机械与电子, 2015(8):14-17 doi: 10.3969/j.issn.1001-2257.2015.08.004Zhou H Q, Wu J J. Study on the method of adaptive slicing contour line based on STL model[J]. Machinery & Electronics, 2015(8):14-17(in Chinese) doi: 10.3969/j.issn.1001-2257.2015.08.004 [10] 周惠群, 吴建军.快速成形CAD模型的轮廓曲线直接分层新算法[J].电加工与模具, 2015(2):43-46 doi: 10.3969/j.issn.1009-279X.2015.02.011Zhou H Q, Wu J J. New direct slicing algorithm for contour curve of CAD model based on rapid prototyping[J]. Electromachining & Mould, 2015(2):43-46(in Chinese) doi: 10.3969/j.issn.1009-279X.2015.02.011 [11] 林洁琼, 王一博, 靖贤, 等.增材制造中STL模型的自适应分层算法研究[J].机械设计与制造, 2018, 2(2):51-53, 57 http://d.old.wanfangdata.com.cn/Periodical/jxsjyzz201802015Lin J Q, Wang Y B, Jing X, et al. Research on adaptive slicing algorithm of STL model in additive manufacturing[J]. Machinery Design & Manufacture, 2018, 2(2):51-53, 57(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxsjyzz201802015 [12] Taufik M, Jain P K. Surface roughness improvement using volumetric error control through adaptive slicing[J]. International Journal of Rapid Manufacturing, 2017, 6(4):279-302 doi: 10.1504/IJRAPIDM.2017.087558 [13] Aremu A O, Brennan-Craddock J P J, Panesar A, et al. A voxel-based method of constructing and skinning conformal and functionally graded lattice structures suitable for additive manufacturing[J]. Additive Manufacturing, 2017, 13:1-13 doi: 10.1016/j.addma.2016.10.006 [14] Patil S, Ravi B. Voxel-based representation, display and thickness analysis of intricate shapes[C]//Proceedings of the 9th International Conference on Computer Aided Design and Computer Graphics. Hong Kong, China: IEEE, 2005: 6 [15] Sylvain L. ICESL: a GPU accelerated CSG modeler and slicer[C]//Proceedings of the 18th European Forum on Additive Manufacturing. Paris, France, 2013: 1-17 [16] Maidin S, Mohamed A S, Akmal S, et al. Feasibility study of vacuum technology integrated fused deposition modeling to reduce staircase effect[J]. Journal of Fundamental and Applied Sciences, 2018, 10(1S):633-645 https://www.ajol.info/index.php/jfas/article/view/168430 [17] 蒋兴方, 王英.基于三角面片法矢量的适应性分层算法[J].湖南工业职业技术学院学报, 2013, 13(1):15-17 doi: 10.3969/j.issn.1671-5004.2013.01.006Jiang X F, Wang Y. Triangular facet normal vector based adaptive slicing algorithm[J]. Journal of Hunan Industry Polytechnic, 2013, 13(1):15-17(in Chinese) doi: 10.3969/j.issn.1671-5004.2013.01.006 [18] Hayasi M, Asiabanpour B. Close to CAD model curved-form adaptive slicing[J]. Rapid Prototyping Journal, 2014, 20(2):133-144 doi: 10.1108/RPJ-06-2012-0054 [19] Huang B, Singamneni S B. Curved Layer Adaptive Slicing (CLAS) for fused deposition modelling[J]. Rapid Prototyping Journal, 2015, 21(4):354-367 doi: 10.1108/RPJ-06-2013-0059 -







 下载:
下载: