Research on Kinematic Calibration Method of Parallel Robot
-
摘要: 并联机器人运动学误差的标定是并联机器人工程应用的主要问题之一,测量位形的选择和辨识算法对参数辨识结果和误差补偿效果有重要影响。工程实践中,为了提高测量效率或者受到测量环境的限制,往往利用布置简单和数量较少的位形获取测量数据,这可能导致所构造的线性回归模型出现强复共线性,为此提出了一种残差比例指标的测量位形优选方法和一种主元分析的几何误差源辨识算法来实现变量空间的降维操作,二者可有效地提高测量效率,改善辨识算法的鲁棒性和抗差能力。通过计算机仿真验证了所提方法正确可行。Abstract: The calibration of kinematic error of parallel robot is one of the main problems in the application of parallel robot. The selection and identification algorithm of measuring positions has important influence on the result of parameter identification and the effect of error compensation. In engineering practice, in order to improve the efficiency of measurement or to be restricted by the measurement environment, measurement data are often obtained with simple position and less number of positions, which may lead to the strong complex collinearity in the linear regression model. Using the means of residual proportion index and the principal component analysis (PCA), the algorithms for optimal measurement configuration selection and robust source error identification are investigated to realize the dimensionality reduction of the variable space, two important issues for improving the measurement efficiency as well as identification accuracy. Computer simulation shows that the proposed method is correct and feasible.
-
表 1 预设的仿真实验方案
方案编号 测量位形优选范围 辨识算法 Ⅰ 上下两层 LS Ⅱ PCA Ⅲ 中间单层 LS Ⅳ PCA 表 2 仿真参数设置
[ξ] [εκ] [fC] [εη] NMC 99.95% 1% 95% 3% 1 000 表 3 测量位形优选结果
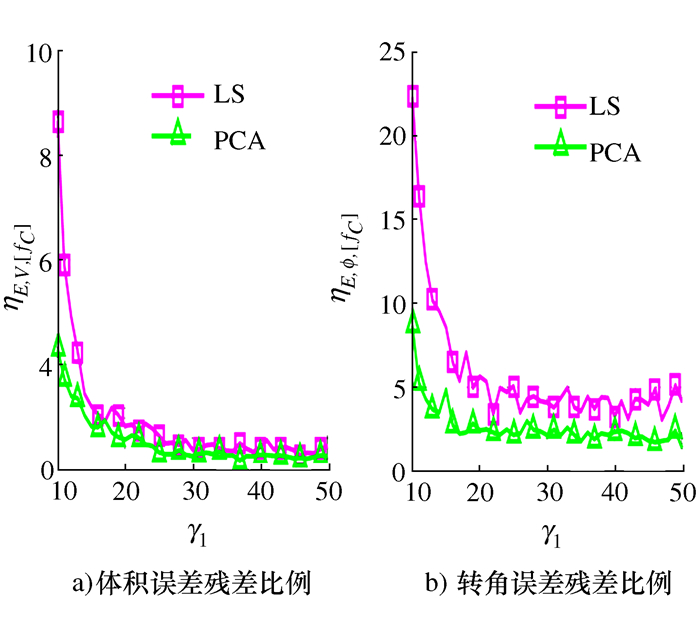
优选指标 LS法 PCA法 κ ηE κ ηE 上下两层 n 21 26 21 25 κn 82.99 81.64 82.99 81.83 ηE, V, 95% 2.86 2.50 2.42 2.33 ηE, ϕ, 95% 5.33 3.48 2.48 2.15 中间单层 n 18 27 18 24 κn 883.2 862.1 883.2 863.2 ηE, V, 95% 49.6 36.5 3.68 2.52 ηE, ϕ, 95% 33.4 18.6 2.54 2.57 表 4 补偿前的体积误差和转角误差
max(ΔV)/mm 
max(|Δϕ|)/(°) 
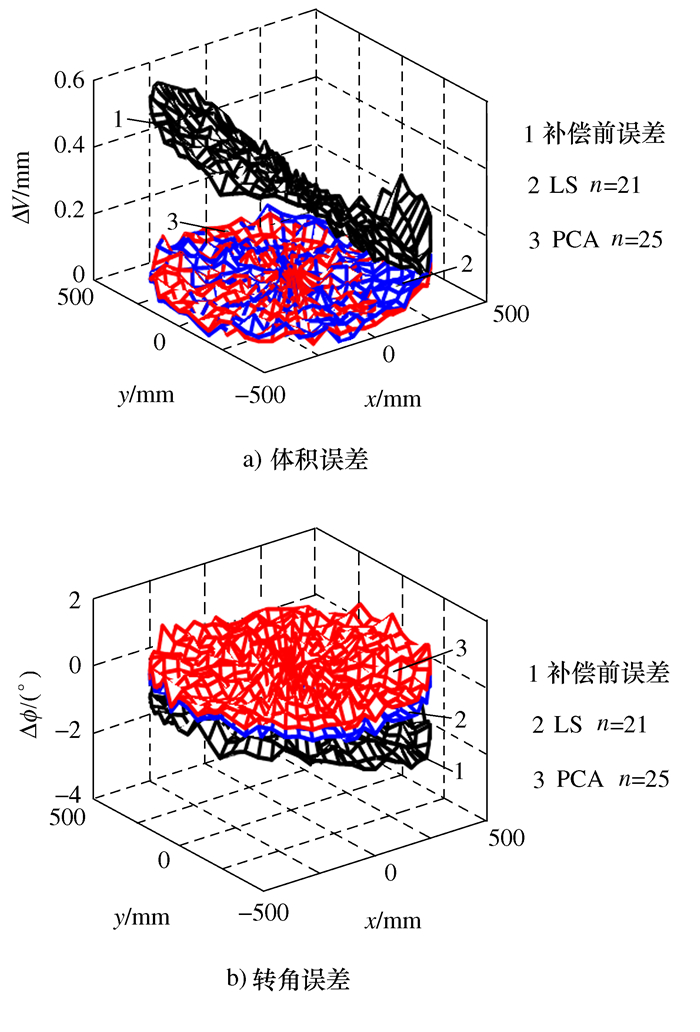
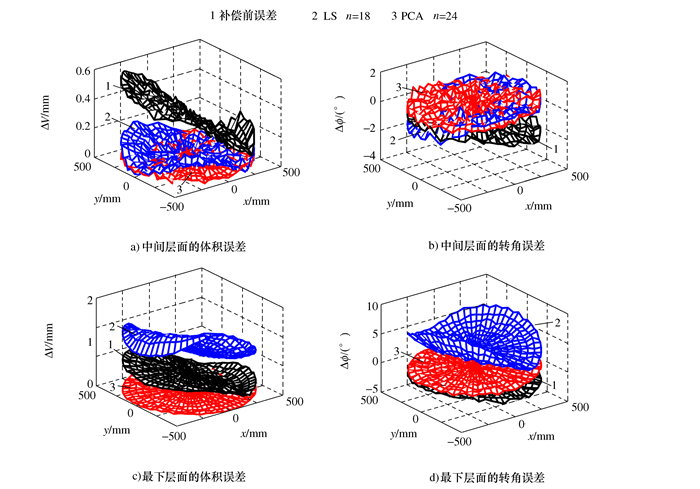
0.728 0.348 2.561 1.113 表 5 补偿后的体积误差和转角误差
方案 算法 指标 n max(ΔV)/
mm
max(|Δϕ|)/(°) 
Ⅰ LS κ 21 0.224 0.105 1.089 0.419 Ⅱ PCA ηE 25 0.117 0.051 0.877 0.229 Ⅲ LS κ 18 1.894 0.879 11.98 6.601 Ⅳ PCA ηE 24 0.128 0.058 0.902 0.267 -
[1] 季晔.少自由度并联机器人机构分析方法研究[M].成都:西南交通大学出版社, 2017Ji Y. Research on mechanism analysis of less freedom parallel robot[M]. Chengdu:Southwest Jiaotong University Press, 2017(in Chinese) [2] 黄田, 李亚, 李思维, 等.一种三自由度并联机构几何误差建模、灵敏度分析及装配工艺设计[J].中国科学:E辑, 2002, 32(5):628-635 http://d.old.wanfangdata.com.cn/Periodical/zgkx-ce200205008Huang T, Li Y, Li S W, et al. Geometric error modeling, sensitivity analysis and assembly process design of a three degree of freedom parallel mechanism[J]. China Science:Series E, 2002, 32(5):628-635(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/zgkx-ce200205008 [3] Huang T, Whitehouse D J, Chetwynd D G. A unified error model for tolerance design, assembly and error compensation of 3-DOF Parallel kinematic machines with parallelogram struts[J]. CIRP Annals, 2002, 51(1):297-301 doi: 10.1016/S0007-8506(07)61521-2 [4] 鲁道夫J.弗洛伊德, 威廉姆J.威尔逊, 平沙.回归分析: 因变量统计模型[M].沈崇麟, 译.重庆: 重庆大学出版社, 2012Freund R J, Wilson W J, Sa P. Regression analysis: statistical modeling of a response variable[M]. Shen C L, trans. Chongqing: Chongqing University Press, 2012(in Chinese) [5] Li T, Sun K, Jin Y, et al. A novel optimal calibration algorithm on a dexterous 6 DOF serial robot-with the optimization of measurement poses number[C]//Proceedings of 2011 IEEE International Conference on Robotics and Automation. Shanghai: IEEE, 2011: 975-981 http://www.mendeley.com/research/novel-optimal-calibration-algorithm-dexterous-6-dof-serial-robot-optimization-measurement-poses-numb/ [6] Borm J H, Meng C H. Determination of optimal measurement configurations for robot calibration based on observability measure[J]. The International Journal of Robotics Research, 1991, 10(1):51-63 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/027836499101000106 [7] Driels M R, Pathre U S. Significance of observation strategy on the design of robot calibration experiments[J]. Journal of Robotic Systems, 1990, 7(2):197-223 doi: 10.1002/rob.v7:2 [8] Nahvi A, Hollerbach J M, Hayward V. Calibration of a parallel robot using multiple kinematic closed loops[C]//Proceedings of 1994 IEEE International Conference on Robotics and Automation. San Diego, CA: IEEE, 1994: 407-412 http://www.mendeley.com/catalog/calibration-parallel-robot-using-multiple-kinematic-closedloops/ [9] Nahvi A, Hollerbach J M. The noise amplification index for optimal pose selection in robot calibration[C]//Proceedings of 1996 IEEE International Conference on Robotics and Automation. Minneapolis: IEEE, 1996: 647-654 http://www.mendeley.com/catalog/noise-amplification-index-optimal-pose-selection-robot-calibration/ [10] Sun Y, Hollerbach J M. Observability index selection for robot calibration[C]//Proceedings of 2008IEEE International Conference on Robotics and Automation. Pasadena, CA: IEEE, 2008: 831-836 http://www.mendeley.com/catalog/observability-index-selection-robot-calibration/ [11] Daney D, Papegay Y, Madeline B. Choosing measurement poses for robot calibration with the local convergence method and Tabu search[J]. The International Journal of Robotics Research, 2005, 24(6):501-518 doi: 10.1177/0278364905053185 [12] Zhou J, Nguyen H N, Kang H J. Selecting optimal measurement poses for kinematic calibration of industrial robots[J]. Advances in Mechanical Engineering, 2014, doi: 10.1155/2014/291389 [13] Joubair A, Nubiola A, Bonev I. Calibration efficiency analysis based on five observability indices and two calibration models for a six-axis industrial robot[J]. SAE International Journal of Aerospace, 2013, 6(1):161-168 doi: 10.4271/2013-01-2117 [14] Zhuang H Q, Wang K, Roth Z S. Optimal selection of measurement configurations for robot calibration using simulated annealing[C]//Proceedings of 1994 IEEE International Conference on Robotics and Automation. San Diego, CA: IEEE, 1994: 393-398 http://www.mendeley.com/catalog/optimal-selection-measurement-configurations-robot-calibration-using-simulated-annealing/ [15] Zhuang H Q, Wu J, Huang W Z. Optimal planning of robot calibration experiments by genetic algorithms[C]//Proceedings of 1996 IEEE International Conference on Robotics and Automation. Minneapolis, MN, USA: IEEE, 1996: 981-986 http://ieeexplore.ieee.org/xpl/abstractAuthors.jsp?arnumber=506836 [16] Chatterjee S, Hadi A S.例解回归分析[M].郑忠国, 许静, 译.北京: 机械工业出版社, 2013Chatterjee S, Hadi A S. Regression analysis by example[M]. Zheng Z G, Xu J, trans. Beijing: China Machine Press, 2013(in Chinese) [17] 王桂增, 叶昊.主元分析与偏最小二乘法[M].北京:清华大学出版社, 2012Wang G Z, Ye H. Principal element analysis and partial least square method[M]. Beijing:Tsinghua University Press, 2012(in Chinese) [18] 周复恭, 黄运成.应用线性回归分析[M].北京:中国人民大学出版社, 1989Zhou F G, Huang Y C. Application of linear regression analysis[M]. Beijing:China Renmin University Press, 1989(in Chinese) [19] 隋立芬, 张超.抗差主成分估计及应用[J].解放军测绘学院学报, 1996, 13(3):195-199 http://d.old.wanfangdata.com.cn/Periodical/slfd201702006Sui L F, Zhang C. Robust principal component estimation and its application[J]. Journal of the PLA Institute of Surveying and Mapping, 1996, 13(3):195-199(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/slfd201702006 [20] 威廉·D·贝里.线性回归分析基础[M].吴晓刚, 译.上海: 格致出版社, 上海人民出版社, 2011Berry W D. Linear regression analysis basis[M]. Wu X G, trans. Shanghai: Truth & Wisdom Press, Shanghai People's Publishing House, 2011(in Chinese) -








 下载:
下载: