功能梯度材料(functionally gradient materials, FGM)是指材料的化学组成、微观结构、原子排列由一侧向另一侧呈连续梯度变化,从而使材料的性质和功能连续地呈梯度变化[1],与传统的复合材料[2-3]相比,FGM具有能够确保应力分布平稳过度、增加不同材料界面的结合强度等特点。FGM最初被设计用作热障材料,后来被拓展到机械工程、光学、核能、土木工程、电子信息及航空航天等诸多领域用来提高产品的实际性能。作为功能和安全设计的前提,FGM结构的具体力学性能,一直倍受人们的关注和重视。Wang等[4]研究了全组分W/Cu功能梯度材料在稳态热载荷下的性能,研究结果表明,梯度过渡层确实可以改善热失配,从而延长疲劳寿命。Shishesaz等[5]基于应变梯度理论,研究了功能梯度纳米圆盘的热弹性行为,主要分析了温度变化对纳米圆盘应力和径向位移的影响。Stathopoulos等[6]研究了用于燃气轮机的功能梯度多层热障涂料的设计,发现功能梯度材料涂层有效地提高了燃气轮机的耐高温性能和热效率。
功能梯度材料在各领域的需求,促进了其制备技术的快速发展,各种制备方法先后出现,为制备具有功能梯度特性的材料提供理论依据和实验支撑。Wan等[7]用等离子产生高温高速热源,把熔融状态的原材料喷涂到基材上形成涂层,原料成分比例不同时可形成不同的功能涂层。但制备出的功能梯度材料有孔隙率高、层间结合力低、强度低的缺点,严重影响了功能梯度材料的性能。其他如SHS法[8]、薄膜积层法[9]等制备出的功能梯度材料也有孔隙率高、易脱落的缺陷。孔隙率对功能梯度材料的各种特性有着很大的影响。对于单相材料中孔隙率与弹性模量关系的理论研究[10-12],研究者们提出了许多能够表示孔隙率与弹性常数关系的方程,这些方程主要适用于小孔隙率时的情况。Phani等[13]根据以往经验推导出了新的方程,该方程能较好地满足具有理想和非理想填充几何模型系统在不同孔隙率时弹性模量的精确理论解。而对于功能梯度材料这类多相材料,Ramakrishana等[14]通过研究孔隙率对体积模量、密度的影响,推导出了适用于大范围孔隙率的有效弹性模量和有效泊松比。Kiran等[15]用有限元法研究了多孔FG磁电弹性板的自由振动特性和静态特性,主要利用修正的混合率公式分析了孔隙率分布对板结构性能的影响以及对板的自由振动和静态特性的影响。Behravan等[16]基于径向和厚度方向上的微分求积和状态空间矢量技术的求解方法,研究了非对称Kerr弹性基础上受非轴对称和非均匀面力作用下变厚度多孔FGM圆板的三维磁弹性解。洪轲等[17]利用本征函数展开法,分析了孔隙率对FGM中Lamb波传播特性的影响。在最近的研究成果中,Fahsi等[18]提出了一种新的准三维剪切变形理论,并在此基础上分析了弹性地基上多孔FGM梁的弯曲、屈曲和自由振动,讨论了2种不同孔隙率分布和长细比对梁的跨中挠度、频率和临界屈曲载荷的影响。诸多研究显示,对含有孔隙FGM的力学性能进行研究具有重要意义,虽然已有一些关于多孔功能梯度结构的静动态问题的研究结果,但研究深度和广度仍显不足。
近些年来,研究者采用一种基于函数的Taylor公式展开来求解微分方程的新方法——微分变换法(differential transformation method, DTM)。该方法的特点是避开直接求未知函数的高阶导数值,通过对微分方程的微分变换得到相邻阶的高阶导数值之间的代数关系,再将初值代入代数关系递推得到不同阶导数的值。由于DTM较高的精度和计算效率,被逐渐引入到许多问题的求解中[19]。目前,对于四边受压多孔功能梯度材料矩形板的DTM求解还鲜有文献报道。
本文基于经典薄板理论,考虑了孔隙和梯度指数对FGM弹性常数的影响,采用DTM研究四边受压多孔FGM矩形板的自由振动和屈曲特性,并在退化后与现有文献值进行对比验证。在计算结果的基础上,进一步分析孔隙率、梯度指数,载荷等参数对多孔FGM矩形板振动特性和临界屈曲载荷的影响。
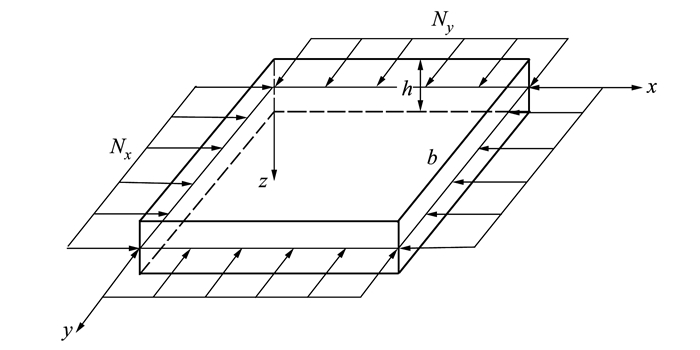
1 多孔FGM矩形板的有效物性参数图 1所示的笛卡尔坐标系中, 多孔FGM矩形板厚度为h, 长度为a, 宽度为b, 四边受到单位压载荷Nx和Ny的作用, xy平面为中面, z轴垂直于中面且与xy轴形成右手螺旋。在y=0和y=b处为简支边界(S), 而在x=0和x=a处可为简支边界(S)、固定边界(C)或自由边界(F)。在本文的问题描述和讨论中, 边界条件按照x=0, y=b, x=a, y=0的顺序给出。
|
| 图 1 四面受压多孔FGM矩形板的几何模型 |
FGM在无孔隙状态下, 其弹性模量E、密度ρ等沿着厚度方向的变化如下[20]
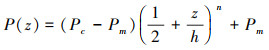
|
(1) |
式中: n为梯度指数; Pc, Pm分别表示无孔隙时陶瓷和金属材料的物性参数。
如果FGM中存在孔隙时, 可以假设孔隙的大小和分布是随机的, 并且介质是连续致密的, 在此基础上得到孔隙率θ与弹性模量E、泊松比ν和密度ρ的关系[12]。
孔隙率
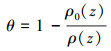
|
(2) |
式中: ρ(z)为致密密度;ρ0(z)为自然密度。
有效泊松比
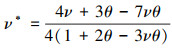
|
(3) |
有效弹性模量
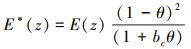
|
(4) |
式中: E(z)和E*(z)分别为θ=0, 0 < θ < 1时的弹性模量;bc=2-3ν。将(1)~(2)式代入(4)式即可得到不同孔隙率下FGM矩形板的有效弹性模量。
2 控制微分方程的无量纲化及DTM变换 2.1 控制微分方程及无量纲化本文中物理中面[21]定义如下
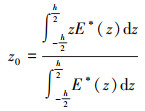
|
(5) |
根据物理中面和经典薄板理论所给出的本构关系, 引入Hamilton原理[22]推导四边受压多孔FGM矩形板运动的控制微分方程。已知Hamilton原理如下
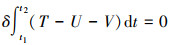
|
(6) |
式中: T, U和V分别为系统的动能、应变能和外力势能; δ为变分符号; t1和t2分别表示系统运动的初始时刻和终止时刻。这里只考虑横向位移, 令w=w(x, y, t), 可得
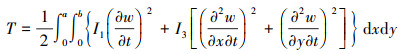
|
(7) |
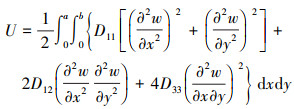
|
(8) |
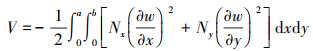
|
(9) |
(7)~(9)式中
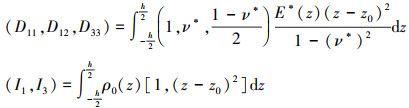
|
分别积分后得到
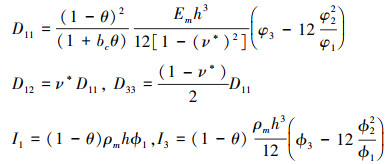
|
式中
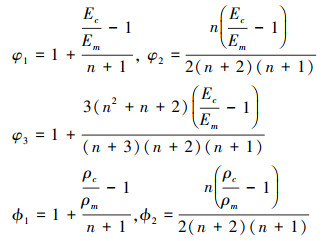
|
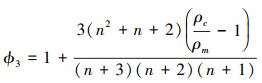
|
式中: D11, D12是抗弯刚度; D33为抗扭刚度, 当n趋近于0时, 抗弯刚度变为Dc, 当n趋近于无穷时, 抗弯刚度变为Dm, I1为多孔FGM矩形板的惯性系数, I3为转动惯量。将(7)~(9)式代入(6)式, 并忽略面内和转动惯性力, 可得四边受压多孔FGM矩形板横向运动的控制微分方程
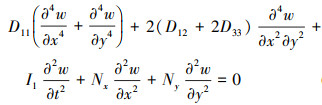
|
(10) |
下边研究y=0和y=b处为简支边界(S)时多孔FGM矩形板做简谐振动的情况, 令w(x, y, t)=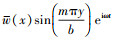
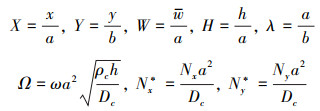
|
式中: λ为长宽比; Ω为无量纲固有频率; Nx*和Ny*为无量纲载荷。则得到四边受压多孔FGM矩形板自由振动时的无量纲控制微分方程
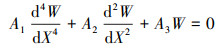
|
(11) |
式中
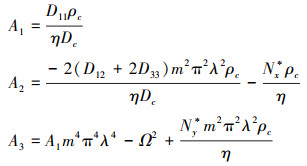
|
由弹性稳定性理论可知, 当临界载荷使得系统发生屈曲时, 其固有频率变为零, 故当(11)式中Ω=0时, 其也可以表示四边受压多孔FGM矩形板屈曲时的无量纲控制微分方程。接下来考虑多孔FGM矩形板在X=0和X=1处的无量纲边界条件, 其形式如(12)~(14)式所示:
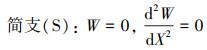
|
(12) |
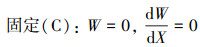
|
(13) |
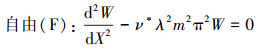
|
(14) |
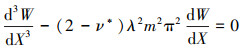
|
解决微分方程的相关问题, 通常采用数值或解析的方法, 这里用一种半解析法——微分变换法(DTM)对问题进行求解, 其原理可参考文献[19]。
依据DTM求解原理, 将四边受压多孔FGM矩形板自由振动与屈曲的无量纲控制微分方程转换为如下的代数方程
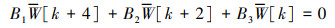
|
(15) |
式中: W[k]为W的微分变换式, k取大于等于零的整数, 系数B1, B2和B3的表达式为
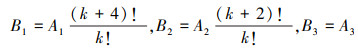
|
边界条件的DTM变换如下
在X=0处:
简支(S):
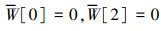
|
(16) |
固定(C):
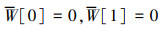
|
(17) |
自由(F):
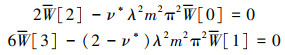
|
(18) |
在X=1处:
简支(S):

|
(19) |
固定(C):
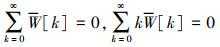
|
(20) |
自由(F):
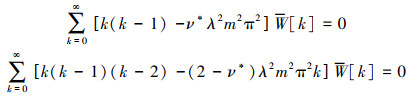
|
(21) |
当X=0时, 令W[0]=c0, W[1]=c1, W[2]=c2, W[3]=c3, 其中c0, c1, c2, c3为待定未知量, 可由边界条件式(16)至(18)确定。将(15)式变为可迭代的形式
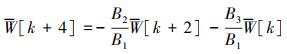
|
(22) |
把c0, c1, c2, c3代入(22)式进行迭代可得W[4], W[5], ⋯, W[r], 通式可表示为W[r]=j0c0+j1c1+j2c2+j3c3, 其中j0, j1, j2, j3是关于c0, c1, c2, c3的系数。当X=1时, 将W[0], ⋯, W[r]代入边界条件(19)至(21)式可得相关边界条件下的特征方程。
结合(15)至(21)式, 边界条件为两边固定两边简支(CSCS)、一边固定三边简支(CSSS)和一边固定一边自由两对边简支(CSFS)的关于无量纲固有频率的特征方程如下
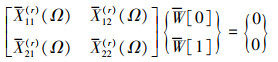
|
(23) |
式中,X11(r), X12(r), X21(r), X22(r)为迭代r次含有未知量无量纲固有频率Ω的多项式, 在以下行列式方程中各量具有相同含义。要使其具有非零解, 必须满足
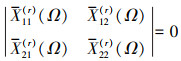
|
(24) |
如果系统发生屈曲时, 无量纲固有频率Ω=0, 此时关于无量纲临界载荷的求解过程类似于(23)至(24)式, 可得
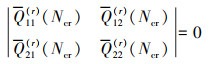
|
(25) |
式中,Ncr为矩形板发生屈曲时的无量纲临界载荷。
对于边界条件为四边简支(SSSS)和一边自由三边简支(SSFS)的关于无量纲固有频率的特征方程如下
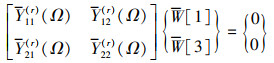
|
(26) |
同理, 要求得无量纲的固有频率和临界屈曲载荷, 必须满足
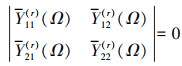
|
(27) |
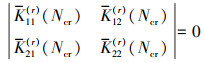
|
(28) |
对于边界条件为两边自由两边简支(FSFS)的情况下, 关于无量纲固有频率的特征方程如下
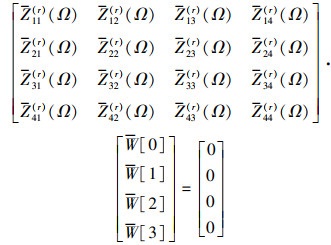
|
(29) |
同理, 要求得无量纲的固有频率和临界屈曲载荷, 必须满足
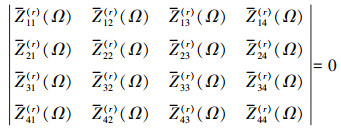
|
(30) |
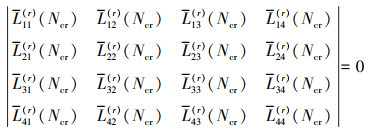
|
(31) |
求解(24)至(28)、(30)、(31)式可获得第r次迭代的第i个特征值(Ω=Ωi(r), Ncr=Ncri(r)), 并且迭代次数与计算精度有关, 可由以下方程确定
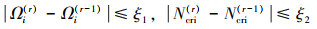
|
式中,ξ1, ξ2为迭代误差限, 取ξ1=ξ2=0.000 001。
3 计算结果及分析DTM的迭代收敛过程可以借助MATLAB编写相关计算程序, 由此求解出四边受压多孔FGM矩形板的自由振动与屈曲问题中无量纲的固有频率和临界载荷。为了验证本文解的正确性与精度, 首先将四边受压多孔FGM矩形板退化为孔隙率为零时的FGM矩形板, 并与已有文献的结果进行比较。FGM矩形板由Al2O3/Al组成, 其物性参数分别为: ρc=3 800 kg/m3, ρm=2 700 kg/m3, Ec=380 GPa, Em=70 GPa, ν=0.3。表 1给出了在CSCS、CSSS、SSSS 3种边界条件下, FGM矩形板长宽比λ分别为0.2, 0.5, 1, Nx*=0, Ny*=0, θ=0, H=0.1, n=0.5时本文DTM解与文献[23]Rayleigh-Ritz法求解的前两阶无量纲固有频率比较, 发现本文结果与文献[23]结果高度一致。
| λ | CSCS | CSSS | SSSS | ||||||
| Ω1 | Ω2 | Ω1 | Ω2 | Ω1 | Ω2 | ||||
| 0.2 | 本文解 | 19.843 4 | 20.444 8 | 13.802 6 | 14.604 2 | 9.015 3 | 10.055 5 | ||
| 文献[23] | 19.843 0 | 20.445 0 | 13.803 0 | 14.605 0 | 9.015 3 | 10.056 0 | |||
| 0.5 | 本文解 | 20.917 5 | 25.427 8 | 15.222 7 | 20.768 8 | 10.835 7 | 17.337 1 | ||
| 文献[23] | 20.918 0 | 25.428 0 | 15.223 0 | 20.771 0 | 10.836 0 | 17.337 0 | |||
| 1.0 | 本文解 | 25.427 8 | 48.081 5 | 20.768 8 | 45.386 1 | 17.337 1 | 43.342 9 | ||
| 文献[23] | 25.428 0 | 48.082 0 | 20.769 0 | 45.398 0 | 17.337 0 | 43.344 0 | |||
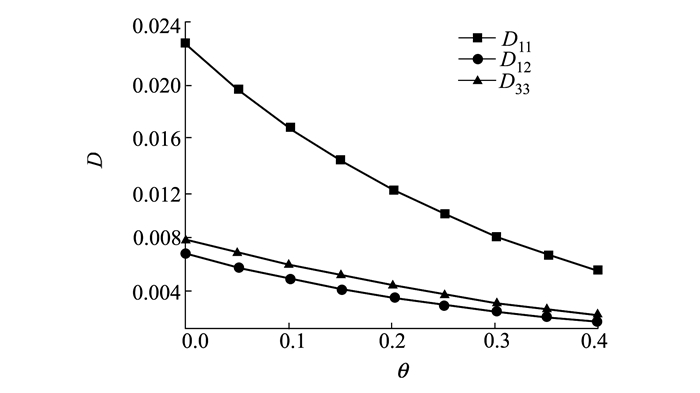
下面计算并分析四边受压多孔FGM矩形板自由振动的无量纲固有频率与临界屈曲载荷。多孔FGM矩形板材料由Si3N4/SUS304组成, 材料的物性参数分别为ρc=2 370 kg/m3, ρm=7 930 kg/m3, Ec=322 GPa, Em=196 GPa, ν=0.3。图 2表示n=1, H=0.1, λ=1时, 孔隙率与刚度的变化关系曲线。结果表明, 随着孔隙率的增大FGM矩形板的刚度减小。
|
| 图 2 孔隙率θ对多孔FGM矩形板刚度D的影响 |
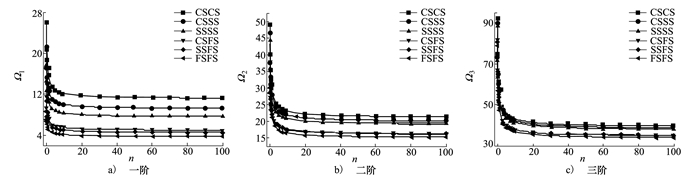
图 3为θ=0.1, H=0.1, Nx*=0, Ny*=0, λ=1时, 在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS边界条件下梯度指数n与前三阶的无量纲固有频率Ω的关系曲线。结果显示, 随着n的增大, 无量纲固有频率Ω总体上在减小。当n在小值范围取值时, 无量纲固有频率减小趋势很剧烈, 当n在较大值范围取值时, 无量纲固有频率变化趋于平缓。当n值一定时, 边界约束越强, 无量纲固有频率越大, 即: CSCS固有频率>CSSS固有频率>SSSS固有频率>CSFS固有频率>SSFS固有频率>FSFS固有频率。
|
| 图 3 梯度指数n对多种边界条件下多孔FGM矩形板Ω的影响 |
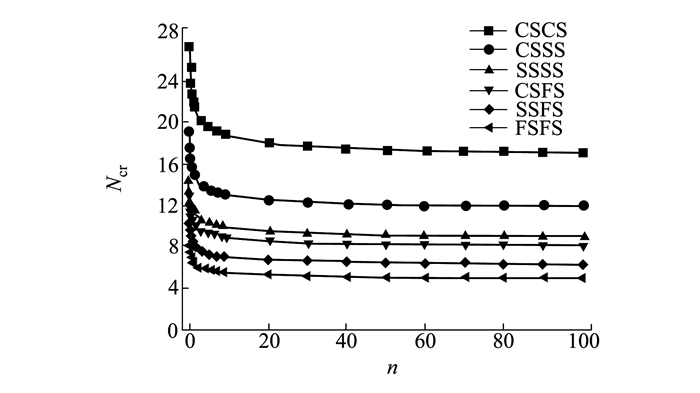
图 4为θ=0.1, H=0.1, Ω=0, λ=1, Nx*=Ny*时, 在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS边界条件下梯度指数n与无量纲临界屈曲载荷Ncr的关系曲线。结果显示, 随着n的增大, 无量纲临界屈曲载荷在减小。n的取值范围从0到100, 当n在较小值范围内取值时, 无量纲临界载荷减小趋势比较剧烈, 当n在较大值范围取值时, 无量纲临界载荷变化较为平缓。当n的值一定时, 边界约束越强, 无量纲临界屈曲载荷也越大。
|
| 图 4 梯度指数n对多种边界条件下多孔FGM |
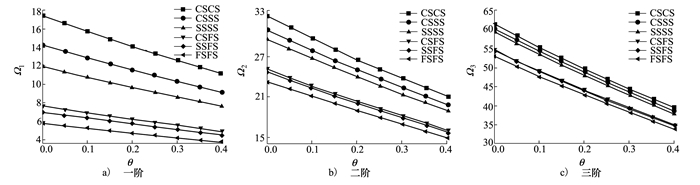
图 5为n=1, H=0.1, Nx*=0, Ny*=0, λ=1时, 在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS边界条件下孔隙率θ与前三阶无量纲固有频率Ω的关系。结果显示, 无量纲固有频率随着孔隙率的增大而减小。当θ一定时, 边界约束越强, 无量纲固有频率越大。
|
| 图 5 孔隙率θ对多种边界条件下多孔FGM矩形板Ω的影响 |
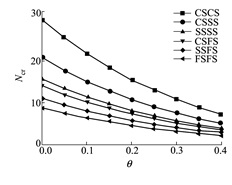
图 6为n=1, H=0.1, Ω=0, λ=1, Nx*=Ny*时, 在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS边界条件下孔隙率θ与无量纲临界屈曲载荷Ncr的关系。结果显示, 无量纲临界屈曲载荷随着孔隙率的增大而减小, 变化趋势呈下凹曲线状。并且, 当θ一定时, 边界约束越强, 无量纲临界屈曲载荷就越大。
|
| 图 6 孔隙率θ对多种边界条件下多孔FGM矩形板Ncr的影响 |
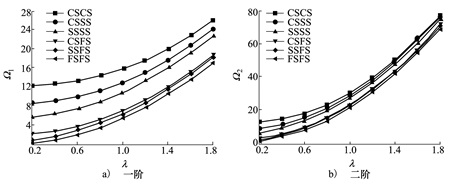
图 7为n=1, θ=0.1, H=0.1, Nx*=0, Ny*=0时, 在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS边界条件下长宽比λ与前两阶无量纲固有频率Ω的关系曲线。结果显示, 无量纲固有频率随着长宽比的增大而增大, 曲线斜率为正, 随着长宽比的增大而增大。当λ一定时, 边界约束越强, 无量纲固有频率越大。
|
| 图 7 长宽比λ对多种边界条件下多孔FGM矩形板Ω的影响 |
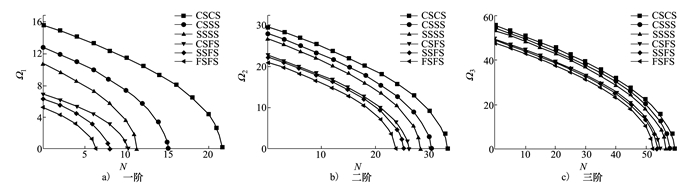
图 8为n=1, θ=0.1, H=0.1, λ=1时, 在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS边界条件下无量纲载荷N=Nx*=Ny*与前三阶无量纲固有频率Ω的关系曲线。结果显示, 无量纲固有频率随着无量纲载荷的增大而减小。值得注意的是, 当无量纲载荷达到无量纲临界屈曲载荷时, 无量纲固有频率变为零。因为结构失稳时振动具有无限大的周期, 即结构固有频率会无限趋近于零, 这与本文结果一致。图中边界约束越强, 无量纲固有频率也越大。
|
| 图 8 无量纲载荷N对多种边界条件下多孔FGM矩形板Ω的影响 |
本文基于经典薄板理论和Hamilton原理建立了四边受压多孔FGM矩形板的自由振动与屈曲问题的控制微分方程并无量纲化, 并运用微分变化法对无量纲控制微分方程及其边界条件进行变换, 通过编写MATLAB计算程序求解出无量纲固有频率和临界屈曲载荷, 进一步分析了参数值的变化对无量纲固有频率和临界屈曲载荷的影响。主要结论如下:
1) 在孔隙率θ一定时, 多孔FGM矩形板无量纲的固有频率Ω与临界屈曲载荷Ncr随着梯度指数n的增大而减小, 随着梯度指数n趋向于无穷大, 多孔矩形板的特性更加趋于多孔金属矩形板的特性。
2) 在梯度指数n一定时, 多孔FGM矩形板无量纲的固有频率Ω与临界屈曲载荷Ncr随着孔隙率θ的增大而减小。
3) 在孔隙率θ与梯度指数n一定时, 多孔FGM矩形板无量纲固有频率Ω随着长宽比λ的增大而增大, 并且随着长宽比λ的增大, 无量纲固有频率Ω增加的速度也在增大。
4) 当无量纲载荷达到无量纲临界屈曲载荷Ncr时, 无量纲固有频率Ω变为零, 此时多孔FGM矩形板的自由振动具有无限大的振动周期, 系统发生失稳。
5) 在相同的条件下, 系统的边界约束越强, 其无量纲固有频率Ω和临界屈曲载荷Ncr就越大。同时, 高阶无量纲固有频率Ω随孔隙率θ和梯度指数n的增大而减小的幅度大于低阶无量纲固有频率Ω。
| [1] |
马涛, 赵忠民, 刘良祥, 等. 功能梯度材料的研究进展及应用前景[J]. 化工科技, 2012, 20(1): 71-75.
MA Tao, ZHAO Zhongmin, LIU Liangxiang, et al. The research development and future application of functionally gradient materials[J]. Science & Technology in Chemical Industry, 2012, 20(1): 71-75. (in Chinese) DOI:10.3969/j.issn.1008-0511.2012.01.019 |
| [2] | REN X, FAN H, WANG C, et al. Coaxial rotatory-freestanding triboelectric nanogenerator for effective energy scavenging from wind[J]. Smart Materials and Structures, 2018, 27(6): 065016. DOI:10.1088/1361-665X/aabe04 |
| [3] | ZENG X, FAN H, ZHANG J. Prediction of the effects of particle and matrix morphologies on Al2O3 particle/polymer composites by finite element method[J]. Computational Materials Science, 2007, 40(3): 395-399. DOI:10.1016/j.commatsci.2007.01.017 |
| [4] | WANG B, ZHU D, LI C, et al. Performance of full compositional W/Cu functionally gradient materials under quasi-steady-state heat loads[J]. IEEE Trans on Plasma Science, 2018, 46(5): 1551-1555. DOI:10.1109/TPS.2018.2803898 |
| [5] | SHISHESAZ M, HOSSEINI M, NADERAN TAHAN K, et al. Analysis of functionally graded nanodisks under thermoelastic loading based on the strain gradient theory[J]. Acta Mechanica, 2017, 228(12): 4141-4168. DOI:10.1007/s00707-017-1939-8 |
| [6] | STATHOPOULOS V, SADYKOV V, PAVLOVA S, et al. Design of functionally fraded multilayer thermal barrier coatings for gas turbine application[J]. Surface and Coatings Technology, 2016, 295: 20-28. DOI:10.1016/j.surfcoat.2015.11.054 |
| [7] | WAN Y P, SAMPATH S, PRASAD V, et al. An advanced model for plasma spraying of functionally graded materials[J]. Journal of Materials Processing Technology, 2003, 137(1/2/3): 110-116. DOI:10.1016/S0924-0136(02)01096-8 |
| [8] | SHCHUKIN A S, VREL D, SYTSCHEV A E. Interaction of NiAl intermetallic during SHS synthesis with Ta substrate[J]. Advanced Engineering Materials, 2018, 20(8): 1701077. DOI:10.1002/adem.201701077 |
| [9] |
黄旭涛, 严密. 功能梯度材料: 回顾与展望[J]. 材料科学与工程, 1997, 15(4): 35-38.
HUANG Xutao, YAN Mi. Review and prospects of functionally gradient materials[J]. Materials Science and Engineering, 1997, 15(4): 35-38. (in Chinese) |
| [10] | SPRIGGS R M. Expression for effect of porosity on elastic modulus of polycrystalline refractory materials, particularly aluminum oxide[J]. Journal of the American Ceramic Society, 1961, 44(12): 628-629. DOI:10.1111/j.1151-2916.1961.tb11671.x |
| [11] | POHANKA R C, RICE R W, WALKER B E. Effect of internal stress on the strength of BaTiO3[J]. Journal of the American Ceramic Society, 1976, 59(1/2): 71-74. |
| [12] | WANG J C. Young's modulus of porous materials[J]. Journal of Materials Science, 1984, 19(3): 809-814. DOI:10.1007/BF00540452 |
| [13] | PHANI K K, NIYOGI S K. Young's modulus of porous brittle solids[J]. Journal of Materials Science, 1987, 22(1): 257-263. DOI:10.1007/BF01160581 |
| [14] | RAMAKRISHNAN N, ARUNACHALAM V S. Effective elastic moduli of porous solids[J]. Journal of Materials Science, 1990, 25(9): 3930-3937. DOI:10.1007/BF00582462 |
| [15] | KIRAN M C, KATTIMANI S. Assessment of porosity influence on vibration and static behaviour of functionally graded magneto-electro-elastic plate: a finite element study[J]. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 2020, 1(44): 61-82. |
| [16] | BEHRAVAN RAD A, SHARIYAT M. Three-dimensional magneto-elastic analysis of asymmetric variable thickness porous FGM circular plates with non-uniform tractions and Kerr elastic foundations[J]. Composite Structures, 2015, 125: 558-574. DOI:10.1016/j.compstruct.2015.02.049 |
| [17] |
洪轲, 袁玲, 沈中华, 等. Lamb波在含孔隙功能梯度材料中传播特性的研究[J]. 声学技术, 2012, 31(6): 539-543.
HONG Ke, YUAN Ling, SHEN Zhonghua, et al. Theoretical research on propagation characteristics of Lamb waves in porous FGMs[J]. Technical Acoustic, 2012, 31(6): 539-543. (in Chinese) DOI:10.3969/j.issn1000-3630.2012.06.001 |
| [18] | FAHSI B, BOUIADJRA R B, MAHMOUDI A, et al. Assessing the effects of porosity on the bending, buckling, and vibrations of functionally graded beams resting on an elastic foundation by using a new refined quasi-3D theory[J]. Mechanics of Composite Materials, 2019, 55(2): 219-230. DOI:10.1007/s11029-019-09805-0 |
| [19] | WATTANASAKULPONG N, CHAROENSUK J. Vibration characteristics of stepped beams made of FGM using differential transformation method[J]. Meccanica, 2014, 50(4): 1089-1101. DOI:10.1007/s11012-014-0054-3 |
| [20] | ELISHAKOFF I, PENTARAS D, GENTILINI C. Mechanics of functionally graded material structures[M]. Singapore: World Scientific Publishing Company, 2016. |
| [21] | ZHANG D, ZHOU Y. A theoretical analysis of FGM thin plates based on physical neutral surface[J]. Computational Materials Science, 2008, 44(2): 716-720. DOI:10.1016/j.commatsci.2008.05.016 |
| [22] | SRIDHAR A, SURIS Y B. Commutativity in Lagrangian and Hamiltonian mechanics[J]. Journal of Geometry and Physics, 2019, 137: 154-161. DOI:10.1016/j.geomphys.2018.09.019 |
| [23] | CHAKRAVERTY S, PRADHAN K K. Free vibration of functionally graded thin rectangular plates resting on Winkler elastic foundation with general boundary conditions using Rayleigh-Ritz method[J]. International Journal of Applied Mechanics, 2014, 6(4): 1450043. DOI:10.1142/S1758825114500434 |


