2. 乔治华盛顿大学 机械与航空工程系, 美国 华盛顿特区 20052
随着计算气动声学的兴起、对复杂流动现象(如旋涡、分离、湍流等)计算需求的增长, 高精度格式因其低耗散、低色散的特性而能够很好地满足上述要求, 逐渐受到了广泛关注[1]。传统的高精度方法由差分方法发展而来, 基于结构网格进行求解, 对复杂外形的适应性不强、不利于网格自适应。由此, 基于非结构/混合网格的高精度方法就具有紧迫的现实需求和广阔的应用前景[2]。近年来发展的基于非结构/混合网格的高精度方法主要包括k-Exact和ENO/WENO等有限体积方法、DG等有限元方法、谱体积(FV)方法、谱差分(SD)方法以及通量重构(FR/CPR)方法。其中, 有限体积类高精度方法在各类网格单元上的实现较为直观, DG和CPR等方法也成功实现了在各类网格单元上的应用[3-5], 但SD方法在此方面进展缓慢。
SD方法最早在三角形单元上提出[6], 随后推广至四边形和六面体单元, 并可在这2种单元上达到任意阶精度[7]。后来发现, 高于二阶的SD格式在三角形单元上存在弱不稳定现象, Balan等[8]通过引入Raviart-Thomas空间得到了三角形单元上的三、四阶稳定格式。Xie等[9]在SD格式中引入分层多项式基, 取代用于构造解多项式的拉格朗日插值基, 并改变了解通量点的分布, 降低了方法对内存的消耗及提高了计算效率。此后, SD方法在除三角形、四边形以及六面体以外的其他网格单元上还未有进展。但SD方法由于采用微分(差分)形式的方程求解, 无需进行复杂的高斯积分, 因此具有计算量小、计算效率高的特点。另外, 传统非结构网格高精度格式是通过多维耦合重构的, 但SD格式在四边形和六面体单元上通过分维度构造格式, 更进一步减小了计算量[10]。因此, 如何将非结构/混合网格与SD方法的优势结合起来, 是SD方法推广过程中的关键。
Liang等[11]通过h-加密方法, 将三角形/四边形混合网格切分为四边形非结构网格, 实现了二维情况下SD方法在混合网格上的应用。对于三维情况:棱柱单元(包括六面体)对于物面边界的正交性良好, 通常用来划分附面层网格; 四面体单元因相邻节点数最少, 具有最好的几何适应性。本文针对三棱柱/四面体混合网格, 通过一阶h-加密方法将其加密为六面体非结构网格, 并通过拉格朗日插值保证对物面处的高精度拟合, 运用六面体单元SD格式, 实现了SD方法在三维混合网格上的应用。
1 数值方法 1.1 SD方法简介考虑如下守恒形式的三维非定常NS方程

|
(1) |
式中,Q是守恒变量; F, G和H分别是沿x, y和z方向的总通量。为了方便方法的实施, 通常将非结构网格单元变换到统一的标准单元上进行计算。例如, 对于物理空间(x, y, z)中全部的六面体单元, 都可通过下式投影到一个标准立方体单元(0≤ξ≤1, 0≤η≤1, 0≤ζ≤1)上

|
(2) |
式中, K是定义一个网格单元的节点数, (xi, yi, zi)是第i个节点的坐标(动网格下随时间变化), Mi是节点对应的形函数。对于每条边都为直线的六面体单元, K=8;对于曲面边界上的网格单元, 20个节点可以定义一个二阶网格单元(12个边中心点, 8个角点); 32个节点可以定义一个三阶网格单元(24个边中心点, 8个角点)。很明显, 相比于低精度网格, 高精度网格能够把具有曲面(边)几何形状的物体拟合得更精确。本文中所有曲面边界都用二阶精度网格进行拟合。
投影关系确定后, 便可得到每个网格单元相应的雅克比矩阵J。由此, NS方程在计算空间中可表示成如下形式
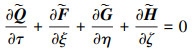
|
(3) |
式中
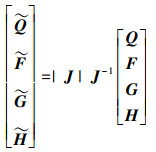
|
(4) |
式中,|J|为变换雅克比矩阵的秩; J-1为其逆矩阵。
SD方法通过在网格单元内部分布的解点(solution points, SPs)与通量点(flux points, FPs)来构造单元内连续的解多项式和通量多项式。对于三阶精度SD格式而言, 标准四边形单元上的解点与通量点分布如图 1所示, 灰色箭头表示通量点构造多项式的方向。

|
| 图 1 三阶SD格式在四边形标准单元上的通量点(方块)与解点(圆形)分布 |
通常, 对于N阶精度SD格式, 需要沿每个坐标轴方向定义N个SPs来构造N-1阶解多项式, N+1个FPs来构造N阶通量多项式(控制方程中通量项要做空间一阶导, 因此所构造的通量多项式需要高一阶)。本文中, SPs选点(Xs)由下式定义

|
(5) |
FPs点(Xs+1/2)选为:单元边界上两点X1/2=0, XN+1/2=1加上单元内部N-1个点(N-1阶Legendre多项式的根)。n阶Legendre多项式可通过如下关系式构造

|
(6) |
式中, 起始的2个多项式为P-1(ξ)=0和P0(ξ)=0。
定义了SPs和FPs后, 可以构造出如下Lagrange插值基
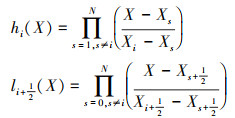
|
(7) |
那么, 解点/通量点构造的解/通量多项式如下

|
(8) |
但如此构造的多项式只在单元内部连续, 在单元边界处不连续。因此, 对于无黏通量, 在边界处用Rusanov黎曼求解器[12]进行求解; 对于黏性通量, 在边界处取平均。
1.2 SD方法的特性分析SD方法由于采用微分(差分)形式的方程求解, 无需进行复杂的高斯积分, 因此具有计算量小、计算效率高的特点。
对于四边形单元和六面体单元, SD方法的构造非常简单直观, 可以达到任意阶精度; 由于在这2种单元上通过(8)式所示分维度构造解/通量多项式, 并结合图 1所示的解点/通量点分布可知, 虚线方框内的4个通量点处的守恒变量值可以直接由方框内3个解点处的值计算得到, 因此其插值将退化为一维, 使得计算效率进一步提高。其他方向(其他变量)的插值同样将退化为一维。
但对于三角形单元, 当阶数大于2时, 传统的SD方法在三角形网格单元上会存在弱不稳定, 其三阶格式解点/通量点分布如图 2a)所示。文献[8]利用Raviart-Thomas空间(RT空间)进行通量插值, 提出了一种适用于三角形单元的稳定的SD方法, 即SDRT方法(三阶格式解点/通量点分布如图 2b)所示)。文章通过线性稳定性分析, 得到了二~四阶SDRT方法稳定的通量点分布。但对于五阶精度及以上的SDRT方法, 至目前为止未有学者给出稳定的通量点分布方式。而且如图 2所示, 三角形中的解点与通量点的分布相互之间并没有联系, 使得每一项插值依然是二维, 即若要得到任一通量点处的守恒变量值, 需要单元上的所有解点共同插值得到, 相比于四边形而言计算量大很多。

|
| 图 2 三阶SD格式在三角形标准单元上的通量点与解点分布 |
下面具体对比六面体与四面体单元的计算效率。对于N阶精度SD格式, 六面体单元中每个坐标轴方向定义N组SPs, N+1组FPs, 那么单元内总共的解点和通量点数量分别为
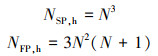
|
(9) |
四面体中定义的解点和通量点数分别为

|
(10) |
式中,下标h和t分别表示六面体和四面体。
对比数值计算过程中由解点上的守恒变量(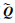
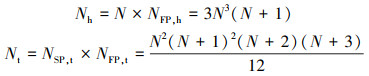
|
(11) |
由上可见, 四面体单元中这一操作计算量的增长率比六面体单元高两阶。当N=4时, 2种单元的自由度之比为NSP, h/NSP, t=3.2, 但这一操作的计算量之比Nh/Nt≈0.686。易知, N=4时完成这一步操作六面体的计算效率是四面体的4.67倍, 并且随着格式精度的提高, 计算效率差距会进一步扩大。
上述分析说明了SD格式在四边形、六面体单元上的突出优势, 以及在其他网格单元上的局限性或者不可行性。对于其他几种差分类的高精度格式(如FR格式), 其四边形/六面体单元的计算效率也同样高于其他网格单元。
1.3 h-加密对于含有三棱柱或四面体单元的非结构/混合网格, 目前SD格式是没法求解的。一种思路是可以通过单元的体心、面心以及边中心进行加密, 将这2种单元切分为若干小六面体单元。并且根据1.2节所述可知, 在精度足够高时, 将三维混合网格拆分成六面体网格不但能够使得全局自由度大大提高, 同时总计算量反而比初始混合网格单元计算量更小。
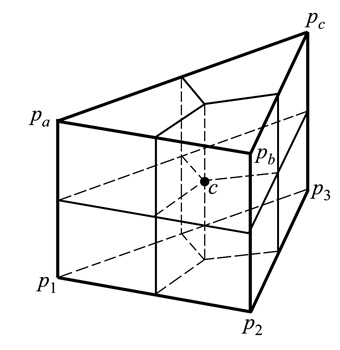
图 3显示了将1个四面体单元进行加密, 切分为4个六面体单元的方法; 图 4显示了将一个三棱柱单元加密为6个六面体单元的方法(粗灰线表示加密之前的网格线, 细黑线是用于加密的网格线)。由图 4可知, 若三棱柱中p1~pa等方向近似垂直于物面, 加密后六面体单元仍能与物面保持良好的正交性。

|
| 图 3 直线加密四面体单元 |
|
| 图 4 直线加密三棱柱单元 |
当一个单元处于曲面边界上时, 加密时需要保证网格的高精度特性。如图 5所示, 以四边形单元为例。假设p1p2处于边界上, 8个方块点定义1个二阶精度的初始四边形单元。进行网格加密时首先应该以这8个方块点为参考, 插值得到如图所示的圆点位置, 以保证将曲面边界刻画得精确, 再将所有的点关联起来, 得到4个加密后的二阶精度四边形单元。同理可对三棱柱和四面体单元进行取点加密。

|
| 图 5 近壁面单元加密示意图 |
本文中初始高精度网格是由Gambit得到的, 更一般的做法可参考文献[13]:首先, 用求解器直接读取目前商用软件生成的直线网格; 然后, 采用非均匀有理B样条曲线/曲面描述几何外形, 作为新生成网格点的参考面; 最后, 用基于径向基函数(或弹性体法、弹簧网格法等)的网格变形方法调整物面周围网格点的位置, 确保网格质量。
2 数值验证本节将用存在解析解的有黏和无黏算例验证SD方法的空间精度; 并计算定常三维圆球绕流以及非定常三维圆柱绕流, 分别与已有文献结果进行对比, 验证求解器的可靠性。所有算例均采用五级四阶显式龙格库塔格式进行时间推进[14]。
2.1 Euler Vortex流动Euler vortex流动被广泛用来测试无黏流动求解器的精度。在Euler vortex流动中, 均匀来流输运一个等熵涡, 这里令z方向速度为0, 用2D Euler vortex流动初始化流场。所有边界都设为周期性边界条件。理想情况下, 流动将一直保持二维, 那么此算例在无穷大区域内的解析解为
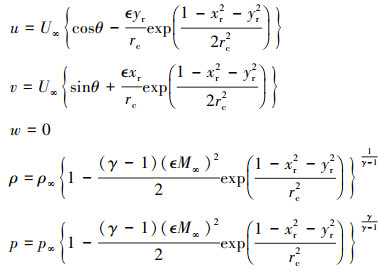
|
(12) |
式中, U∞, ρ∞, p∞和M∞分别为均匀流的速度、密度、压力和马赫数; θ为均匀流方向与x轴的夹角; 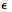
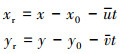
|
(13) |
式中,(u, v)=(U∞cosθ, U∞sinθ)均匀流的速度分量, (x0, y0)代表涡的初始位置。
在本仿真中, 均匀来流的流动参数是:(U∞, ρ∞)=(1, 1), 马赫数M∞=0.3, 涡随着均匀流沿θ=π/6方向运动。计算域为0≤x, y≤10, 0≤z≤2。仿真初始时刻, 将强度和尺寸分别为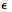

|
| 图 6 用于Euler Vortex流动仿真的30/90个三棱柱/四面体混合单元网格加密示意图 |
图 7显示了t=2.3时刻, 用四阶精度格式在网格量为200/568的网格上仿真的瞬时密度云图。此时, 涡已经由初始时刻所处的流场中心向右上角运动了一段距离, 涡形状保持得非常好。

|
| 图 7 t=2.3时刻Euler Vortex流动密度云图 |
通过密度的L1和L2误差, 进一步验证了计算精度。2个误差定义如下
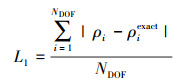
|
(14) |
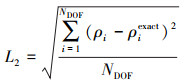
|
(15) |
式中, ρi和ρiexact分别是第i个自由度处的数值解和解析解; NDOF是全局的自由度数量。对于1套具有Nprism个三棱柱单元和Ntet个四面体单元的初始网格, 若用一阶h-加密, 并采用N阶精度格式, 则其自由度为

|
(16) |
表 1给出了t=2.3时刻上述3套网格在三阶和四阶格式下的误差和精度。精度的计算依据如下公式
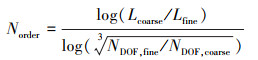
|
(17) |
| 格式 | 网格量 | L1误差 | 精度 | L2误差 | 精度 |
| 三阶 | 30/90 | 2.47×10-4 | - | 4.78×10-4 | - |
| 200/568 | 4.19×10-5 | 2.86 | 9.62×10-5 | 2.58 | |
| 1 600/4 451 | 5.64×10-6 | 2.91 | 1.47×10-6 | 2.73 | |
| 四阶 | 30/90 | 5.02×10-5 | - | 1.15×10-4 | - |
| 200/568 | 3.05×10-6 | 4.29 | 9.58×10-6 | 4.00 | |
| 1 600/4 451 | 1.77×10-7 | 4.33 | 4.63×10-7 | 4.63 |
从表中可见, 误差随着网格的加密逐渐减小。当使用三阶精度格式时, 数值计算得到的精度阶数略小于3;四阶精度格式得到的结果略大于4。因此, 求解器在此无黏流动中达到了设计精度。
2.2 Taylor-Couette流动Taylor-Couette流动形成于具有相对转动的2个同心圆形壁板之间。当流场雷诺数很小(相对角速度差较小)时, Taylor-Couette流动将达到一个稳态, 即黏性效应能平衡惯性。平衡状态下流动的周向速度会具有如下解析表达式

|
(18) |
式中,r为半径; ω为角速度; 下标i和o分别表示内壁板和外壁板。
在当前仿真中, 内壁板半径为ri=1, 以角速度ωi=1逆时针转动; 外壁板半径为ro=2, 角速度ωo=0;2个壁板都视为等温壁。雷诺数的值依赖于ri, ωi以及流体黏性(假设为常量), 取为Re=10。内壁板处的马赫数设为Mi=0.1。用网格量分别为96/162, 768/826和6 144/5 667的3套三棱柱/四面体混合网格进行精度测试, 内、外壁板附近都用三棱柱网格单元进行划分, 中间区域用四面体单元进行划分。图 8a)显示了第一套网格划分情况, 图 8b)是一阶h-加密后得到的计算网格。

|
| 图 8 用于Taylor-Couette流动仿真的96/162个三棱柱/四面体混合单元网格加密示意图 |
图 9显示了计算达到稳定状态后, 四阶精度格式在网格量为768/826的网格上仿真的密度云图。可以看出, 云图由一系列层次分明的同心圆组成, 与预期一致。

|
| 图 9 仿真稳定后Taylor-Couette流动密度云图 |
表 2给出了上述3套网格在三阶和四阶精度格式下仿真稳定后由x方向速度分量计算的得到的误差和精度。从表中可见, 三阶和四阶格式都达到了设计精度, 说明求解器对于黏性流体也能够实现预期精度的数值模拟。
| 格式 | 网格量 | L1误差 | 精度 | L2误差 | 精度 |
| 三阶 | 96/162 | 1.58×10-3 | - | 1.70×10-3 | - |
| 768/826 | 2.49×10-4 | 2.97 | 2.96×10-4 | 2.81 | |
| 6 144/5 667 | 3.50×10-5 | 2.92 | 4.61×10-5 | 2.76 | |
| 四阶 | 96/162 | 5.10×10-4 | - | 4.89×10-4 | - |
| 768/826 | 3.65×10-5 | 4.24 | 3.55×10-5 | 4.22 | |
| 6 144/5 667 | 1.91×10-6 | 4.39 | 2.03×10-6 | 4.25 |
此算例模拟三维圆球黏性绕流, 并与实验结果进行对比, 验证求解器的有效性。
计算状态为马赫数0.3, 雷诺数118, 此问题实验得到的阻力系数为1.01[15]。计算域为10×10×10的立方体, 将半径为0.5的圆球置于流场中心, 圆球表面视为绝热壁, 前端和后端分别为流入和流出边界, 四周为对称边界条件。图 10显示了圆球表面以及其垂直于z向的子午面网格加密示意图, 初始网格包含了240/4 138个三棱柱/四面体混合网格单元, 加密成为包含17 992个六面体网格单元的非结构网格。

|
| 图 10 定常天天维圆球绕流网格加密示意图 |
表 3给出了采用不同精度格式的阻力系数计算结果:从表中可以看出, 随着格式精度的提高, 计算值与实验值越来越接近, 说明随着精度的增加, 计算结果是收敛的; 四阶格式的计算结果与实验值已经基本一致了。
图 11显示了用四阶格式计算得到的马赫数云图、压力云图以及流线。云图与阻力系数结果验证了求解器的可靠性。

|
| 图 11 定常三维圆球绕流计算结果 |
此算例模拟非定常三维圆柱绕流, 并与已有文献仿真结果进行对比。
圆柱直径d=1, 轴向长度为10d。计算域如图 12所示:入口边界距圆柱轴线20d; 出口边界距圆柱轴线80d; 上下边界取为对称边界条件, 分别距圆柱轴线20d; 左右边界取为周期性边界条件。初始网格包含了1 200/26 112个三棱柱/四面体网格单元, 图 13显示了圆柱表面以及一侧周期边界上的网格加密示意图。计算状态为马赫数0.2, 雷诺数150, 计算终止时间为600 s。

|
| 图 12 非定常三维圆柱绕流计算域示意图 |

|
| 图 13 非定常三维圆柱绕流网格加密示意图 |
图 14给出了某一瞬时流场的Q-准则涡量等值面云图和垂直于圆柱轴线的中垂面Q-准则涡量云图。可以看出, 此状态下圆柱后面会出现卡门涡街, 但等值面沿z方向没有可见的变化, 说明没有出现明显的三维效应。因此, 表 4给出了文献[13-16]中相同状态下二维非定常圆柱绕流计算结果, 可知本文计算结果与之接近。

|
| 图 14 非定常三维圆柱绕流计算结果(Q-准则涡量云图) |
本文提出了一种针对三维非结构/混合网格的高精度谱差分格式求解方法。与传统的高精度谱差分格式求解方法相比, 可以得到以下结论:
1) 运用一阶h-加密方法处理三棱柱/四面体混合网格, 运用高精度插值保证物面的曲面特性, 实现了SD格式在混合网格上的应用;
2) 方法能够将六面体单元上SD格式的突出优势与混合网格良好的几何适应性完美地结合起来;
3) 数值验证表明该方法保持了SD格式的高精度特性;
4) 本文所采用的网格加密思路也适用于其他高精度格式(如FR格式), 可以避免在各种网格单元上构造稳定格式的需求, 或达到减少计算量的效果。
| [1] |
刘秋洪, 覃梦阳, 毛义军, 等. 非紧致气动噪声传播的研究进展与分析[J]. 空气动力学学报, 2018, 36(3): 440-448.
LIU Qiuhong, QIN Mengyang, MAO Yijun, et al. A Review on the Propagation of Non-Compact Aerodynamic Sound[J]. Acta Aerodynamica Sinica, 2018, 36(3): 440-448. (in Chinese) DOI:10.7638/kqdlxxb-2017.0216 |
| [2] | WANG Z J. A Perspective on High-Order Methods in Computational Fluid Dynamics[J]. Science China Physics Mechanics & Astronomy, 2016, 59(1): 614701-614701. |
| [3] | LI W, PAN J, REN Y X. The Discontinuous Galerkin Spectral Element Methods for Compressible Flows on Two-Dimensional Mixed Grids[J]. Journal of Computational Physics, 2018, 364: 314-346. DOI:10.1016/j.jcp.2018.03.001 |
| [4] |
马明生, 龚小权, 邓有奇, 等. 一种适用于非结构网格的间断Galerkin有限元LU-SGS隐式方法[J]. 西北工业大学学报, 2016, 34(5): 754-760.
MA Mingsheng, GONG Xiaoquan, DENG Youqi, et al. An Implicit LU-SGS Scheme for the Discontinuous Galerkin Method on Unstructured Grids[J]. Journal of Northwestern Polytechnical University, 2016, 34(5): 754-760. (in Chinese) DOI:10.3969/j.issn.1000-2758.2016.05.003 |
| [5] | WITHERDEN F D, VERMEIRE B C, VINCENT P E. Heterogeneous Computing on Mixed Unstructured Grids with PyFR[J]. Computers & Fluids, 2015, 120: 173-186. |
| [6] | LIU Y, VINOKUR M, WANG Z J. Spectral Difference Method for Unstructured GridsⅠ:Basic Formulation[J]. Journal of Computational Physics, 2006, 216(2): 780-801. DOI:10.1016/j.jcp.2006.01.024 |
| [7] | SUN Y, WANG Z J, LIU Y. High-Order Multidomain Spectral Difference Method for the Navier-Stokes Equations[J]. Communications in Computational Physics, 2007, 2(2): 310-333. DOI:10.2514/6.2006-301 |
| [8] | BALAN A, MAY G, SCHÖBERL J. A Stable High-Order Spectral Difference Method for Hyperbolic Conservation Laws on Triangular Elements[J]. Journal of Computational Physics, 2012, 231(5): 2359-2375. DOI:10.1016/j.jcp.2011.11.041 |
| [9] | XIE L, XU M, ZHANG B, et al. A New Spectral Difference Method Using Hierarchical Polynomial Bases for Hyperbolic Conservation Laws[J]. Journal of Computational Physics, 2015, 284(C): 434-461. |
| [10] | YU M, WANG Z J, LIU Y. On the Accuracy and Efficiency of Discontinuous Galerkin, Spectral Difference and Correction Procedure via Reconstruction Methods[J]. Journal of Computational Physics, 2014, 259: 70-95. DOI:10.1016/j.jcp.2013.11.023 |
| [11] | LIANG C, JAMESON A, WANG Z J. Spectral Difference Method for Compressible Flow on Unstructured Grids with Mixed Elements[J]. Journal of Computational Physics, 2009, 228(8): 2847-2858. DOI:10.1016/j.jcp.2008.12.038 |
| [12] | RUSANOV V V. Calculation of Interaction of Non-Steady Shock Waves with Obstacles[J]. Journal of Computational Math Physics USSR, 1961, 1: 261-279. |
| [13] |
谢亮.计算流体力学中的高精度数值计算方法研究[D].西安: 西北工业大学, 2016 XIE Liang. Research of High Order Numerical Methods in Computational Fluid Dynamics[D]. Xi'an, Northwestern Polytechnical University, 2016(in Chinese) |
| [14] | RUUTH S. Global Optimization of Explicit Strong-Stability-Preserving Runge-Kutta Methods[J]. Mathematics of Computation, 2006, 75(253): 183-207. |
| [15] | TANEDA S. Experimental Investigation of the Wake Behind a Sphere at Low Reynolds Numbers[J]. Journal of the Physical Society of Japan, 1956, 11(10): 1104-1108. DOI:10.1143/JPSJ.11.1104 |
| [16] | ZHANG L, LIU W, LI M, et al. A Class of DG/FV Hybrid Schemes for Conservation Law Ⅳ:2D Viscous Flows and Implicit Algorithm for Steady Cases[J]. Computers & Fluids, 2014, 97(6): 110-125. DOI:10.1016/j.compfluid.2014.04.002 |
2. Department of Mechanical and Aerospace Engineering, George Washington University, Washington, DC 20052, USA


