2. 河南科技大学 河南省机械设计及传动系统重点实验室, 河南 洛阳 471003;
3. 洛阳LYC轴承有限公司 航空精密轴承国家重点实验室, 河南 洛阳 471003
滚动轴承是应用广泛的重要机械基础件, 广泛应用于复杂的精密机械中, 如航空发动机, 精密机床、磁盘和陀螺仪等, 其旋转精度往往直接决定机械系统的精度[1-2]。在轴承零件加工过程中不可避免产生几何误差, 而轴承零件几何误差又是导致轴承回转误差的重要因素之一[3]。因此, 深入研究轴承零件几何误差对轴承回转误差的作用机理, 对提升高精度轴承的设计水平是很有意义的。
目前, 关于滚动轴承零件几何误差对轴承性能的影响, 研究工作主要集中在轴承非重复性跳动、轴心轨迹、动态性能和旋转精度等方面。Tada等[4]和袁幸等[5]建立了滚动轴承非重复性跳动计算模型, 研究了沟道和钢球波纹度及钢球个数对轴承非重复性跳动影响。Jang等[6]分析了磁盘用的球轴承非重复性跳动产生的机理, 并研究了轴承非重复性跳动传递到磁盘的路径。Noguchi等[7-12]建立了考虑轴承零件圆度误差及钢球直径差的球轴承非重复性跳动计算方法, 分析了轴承沟道和滚子表面圆度误差、钢球个数和钢球直径差及排布对球轴承非重复性跳动的影响规律。马方波等[13]建立了考虑滚子直径误差的球面滚子轴承轴心轨迹的计算模型, 研究了单个和多个滚子直径误差对球面滚子轴承轴心轨迹的影响。Okamoto等[14]建立了基于外圈沟道圆度误差的球轴承轴心轨迹预测模型, 分析了钢球个数、滚动体尺寸误差和沟道圆度误差对轴心轨迹大小及形状的影响。Gunhee等[15]建立了考虑轴承零件波纹度的转子——轴承系统的非线性动力学模型, 分析了轴承径向游隙、零件的波纹度、阻尼和不平衡力对轴承动态特性的影响。Xu等[16]和Kankar等[17]提出了一种球轴承动态性能计算模型, 分析了轴承零件波纹度和微观缺陷对轴承动态性能的影响。Patel等[18]和Wang等[19]建立了圆柱滚子轴承动态性能计算模型, 分析了滚道波纹度及滚道缺陷对轴承振动的影响。Chen等[20-21]建立了基于滚道圆度误差和滚子尺寸误差的轴承径向跳动计算模型, 分析了轴承滚道圆度误差和滚子尺寸误差对轴承旋转精度的影响。Bhateja等[22]建立了考虑滚子尺寸差的无保持架空心圆柱滚子轴承旋转精度预测模型, 研究了空心圆柱滚子尺寸误差及滚子圆周间隙对空心圆柱滚子轴承旋转精度的影响规律。在本课题组前期轴承旋转精度研究工作中, 建立了基于轴承内圈滚道圆度误差的轴承内圈径向跳动计算模型, 分析了内圈滚道圆度误差对内圈径向跳动及其历程、运动轨迹的影响[23-24]; 建立了考虑轴承外圈滚道圆度误差的轴承外圈径向跳动计算模型, 分析了外圈滚道圆度误差和滚子个数对轴承外圈径向跳动的影响[25-26]。
目前, 轴承旋转精度的研究主要集中在内、外圈滚道几何误差等因素对轴承跳动的影响方面, 而忽略了滚子几何误差的影响。滚子作为连接内圈与外圈的关键零件, 与内、外圈共同作用, 从而实现轴承的回转运动。因此, 研究滚子几何误差对轴承旋转精度的影响是很有必要的。为此, 考虑内圈滚道、外圈滚道和滚子几何误差, 同时还考虑由于轴承零件几何误差导致的滚子与滚道接触点变化, 提出了轴承内圈旋转精度数值模型, 分析滚子圆度误差、不同几何误差滚子排布方式、滚子个数对轴承内圈在径向平面内跳动的影响规律, 为轴承零件几何误差的控制和分配提供理论依据。
1 轴承内圈旋转精度数值模型滚动轴承旋转精度为轴承在无载、低转速条件下旋转套圈的安装定位表面位置与理想位置的接近程度, 它既反映了轴承的制造精度, 也反映了轴承运转时的工作性能[27]。国家标准《滚动轴承测量和检验的原则及方法》规定了轴承旋转精度的测量条件和方法。在测量轴承旋转精度时, 测试轴承在无载和低转速条件下运转。所谓“无载”是指轴承不承受工作载荷, 仅承受很小的测量载荷, 从而保证轴承部分滚子与内外圈滚道完全接触, 但不能使轴承零件间产生明显的弹性变形。所谓“低转速”是指轴承转速很慢, 近而避免因轴承零件间的冲击引起的轴承振动, 从而保证测量精度。基于以上轴承旋转精度的测量工况, 本文以圆柱滚子轴承零件几何和运动关系及力平衡原理为基础, 提出了内圈旋转时考虑轴承零件几何误差的轴承内圈旋转精度数值模型, 用于预测具有不同几何误差的轴承零件装配后成品轴承内圈在径向平面内的跳动。本文所提的数值模型基于以下假设:
1) 不考虑滚道和滚子表面轴向形状误差;
2) 滚子与滚道之间为纯滚动;
3) 滚子在圆周方向等间隔分布。
轴承内圈旋转精度数值模型建立的过程如下:①内圈转动一个设定步长角度, 获得轴承内圈滚道、外圈滚道和滚子轮廓半径方程; ②分别使位于轴承下半部的所有滚子沿径向移动, 直至与外圈滚道接触, 计算此时的滚子圆心坐标; ③任意给定不同内圈位置, 判断每个滚子与内圈滚道的位置关系(接触、分离和干涉), 获得不同位置处内圈滚道的接触状态; ④根据不同位置处内圈滚道的接触状态, 利用提出的内圈稳定状态判据找出内圈的位置, 从而获得内圈转动一个步长对应的圆心坐标。内圈继续旋转一个步长, 重复以上相关计算。以此类推, 内圈旋转几周, 获得不同旋转角度对应的内圈圆心坐标; ⑤遍历所有内圈位置, 计算轴承内圈圆心与外圈圆心之间的距离, 找出这个距离的最大值和最小值, 两者之差即为轴承内圈在径向平面内的跳动量, 简称为轴承内圈跳动量。轴承内圈旋转精度数值模型计算流程如图 1所示, 下面对该数值模型中的重要步骤作以阐述。
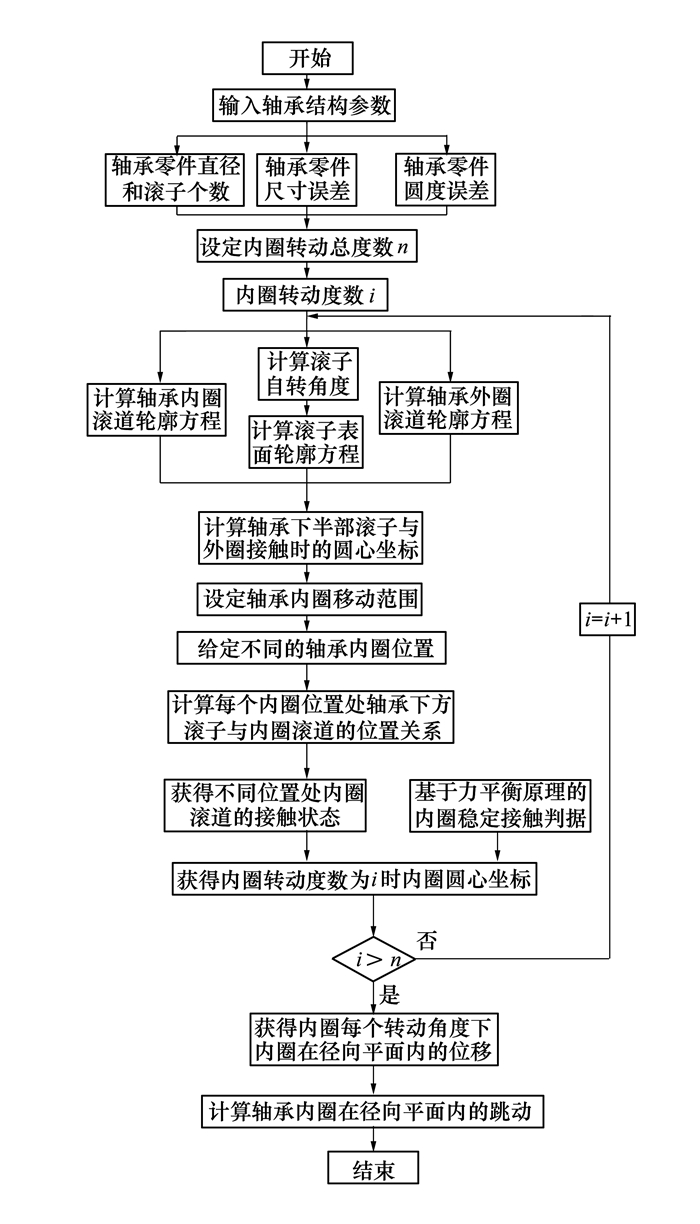
|
| 图 1 轴承内圈旋转精度数值模型计算流程图 |
由于轴承零件几何误差的存在, 滚动体和套圈滚道轮廓均为非圆轮廓, 如图 2所示。
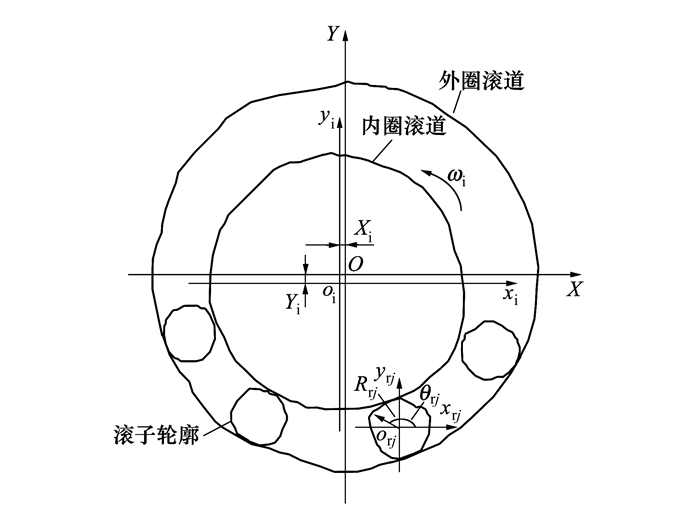
|
| 图 2 轴承几何关系 |
轴承的整体笛卡儿坐标系XOY固定于轴承外圈圆心; 局部坐标系xioiyi固定于内圈圆心, xiyi平面与轴承内圈滚道中剖面重合, 且坐标系只随内圈平移; 另一个局部坐标系xrjorjyrj固定于第j个滚子圆心, 其坐标轴与整体坐标轴平行, 且坐标系仅随滚子平移。当轴承内圈旋转且外圈固定时, 由于重力的作用, 轴承内圈向下运动, 并最终达到稳定状态。此时, 内圈圆心由O点移动至oi点, 在水平方向的位移为Xi, 在竖直方向的位移为Yi。
在轴承整体坐标系XOY中, 当内圈逆时针转动α角时, 第j个滚子绕其轴线顺时针自转, 同时也绕轴承轴线公转, 第j个滚子公转至新的位置, 其自转及公转的角度、位置角分别为[3]:
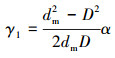
|
(1) |
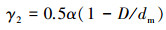
|
(2) |

|
(3) |
式中, α为内圈转动的角度; γ1, γ2分别为滚子自转和公转角度; dm为轴承节圆直径; D为滚子直径; βj为第j个滚子的位置角; 其中,j为滚子序号(j=1, 2, …, Z); Z为滚子个数。
为计算轴承的旋转精度, 需将每个轴承零件廓形曲线进行数学表征。傅里叶级数是由一系列三角函数线性叠加组成, 常用于表征复杂的零件表面廓形。利用傅里叶级数表征轴承零件圆度误差, 其中, 阶次表示轴承零件的几何形状, 幅值表示轴承零件轮廓偏离理想圆的峰值。在xioiyi坐标系下内圈滚道轮廓半径Ri(θi)、在XOY坐标系下外圈滚道轮廓半径Re(θe)、在xrjorjyrj坐标系下第j个滚子轮廓半径Rrj(θrj)的极坐标方程分别表示为:
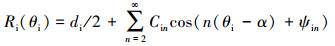
|
(4) |
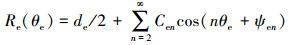
|
(5) |
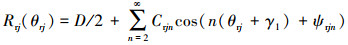
|
(6) |
式中, θi为在xioiyi坐标系下内圈滚道轮廓上任一点的位置角; θe为在XOY坐标系下外圈滚道轮廓上任一点的位置角; θrj为在xrjorjyrj坐标系下滚子轮廓上任一点的位置角; di, de和D分别为内圈滚道、外圈滚道和滚子直径; Cin, Cen和Crjn分别为内圈滚道、外圈滚道和第j个滚子表面轮廓第n阶谐波幅值; ψin, ψen和ψrjn分别为内圈滚道、外圈滚道和第j个滚子表面轮廓第n阶谐波初始相位角。
1.2 滚子圆心坐标的计算当轴承外圈固定时, 在重力作用及保持器兜孔约束下, 轴承下半部的滚子沿径向移动, 最终与外圈滚道接触。为获得此时的滚子圆心坐标, 假设滚子初始位置在轴承节圆直径处, 并按设定步长沿径向移动, 直至与外圈滚道接触, 获得此时滚子圆心到外圈圆心的距离, 从而根据几何关系计算出滚子圆心坐标。这里获得滚子与外圈滚道的位置关系是关键, 为此作者提出了以滚子表面到外圈滚道最短距离作为滚子与外圈滚道位置关系的判断标准, 据此标准判断出滚子与外圈滚道是否接触, 从而计算出滚子的圆心坐标。
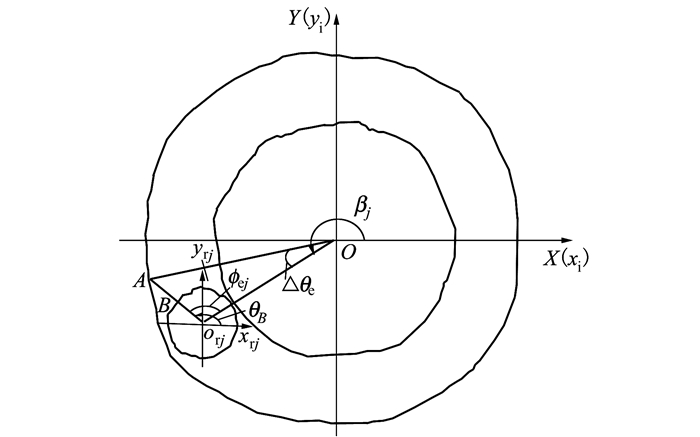
当内圈转动α角度时, 第j个滚子移至某个位置时, 滚子与外圈滚道几何关系如图 3所示。
|
| 图 3 滚子与外圈滚道几何关系 |
由几何关系可知, 外圈滚道上任一点A与滚子表面上任一点B的距离为:
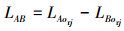
|
(7) |
式中, LAorj为第j个滚子圆心到外圈滚道上A点的距离, 由(8)式计算; LBorj为第j个滚子自转γ1角度后的B点轮廓半径, 由(6)式计算, 其中, B点的位置角可通过几何关系推导获得, 其值与滚子所在象限及B的位置有关, 当滚子处于第三象限且B点处于A点下方时, 如图 3所示, B点的位置角由(9)式计算。
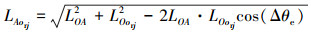
|
(8) |
式中, LOA为外圈滚道上A点的轮廓半径, 由(5)式计算; LOorj为给定的外圈圆心到第j个滚子圆心的距离; Δθe为外圈滚道上A点与第j个滚子圆心在圆周方向上的夹角, -arcsin(D/de)≤Δθe≤arcsin(D/de)。

|
(9) |
式中, 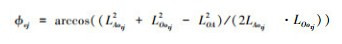
在(7)式中, 当Δθe在一定范围内变化时, 在外圈滚道上存在一个A点, 滚子表面上存在一个B点, 使A点到B点的距离LAB最短, 即为滚子表面到外圈滚道的最短距离LABmin。当LABmin>ε(ε设定的正极小值)时, 则认为滚子与外圈滚道未接触, 继续移动滚子; 当|LABmin|<ε时, 则认为滚子与外圈滚道接触, 获得此时滚子圆心到外圈圆心的距离, 从而计算出滚子的圆心坐标, 如(10)式所示。以此类推, 计算出轴承下半部每个滚子与外圈滚道接触时的圆心坐标。
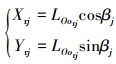
|
(10) |
根据上一节的计算, 获得了轴承下方滚子与外圈滚道处于接触状态时的圆心坐标。在此基础上, 在平面内移动内圈, 则轴承下半部滚子与内圈滚道的位置关系(接触、分离和干涉)随着内圈位置的变化而变化。由于无法获取内圈实际的移动范围, 故设定一个包含该范围的区域。在此区域内任意给定一个内圈位置, 计算每个滚子表面到内圈滚道的最短距离, 据此判断每个滚子与内圈滚道的位置关系, 获得此位置处内圈滚道接触状态。与1.2节的做法相似, 这里也提出了滚子表面到内圈滚道最短距离计算方法, 以判断滚子与内圈滚道的位置关系。
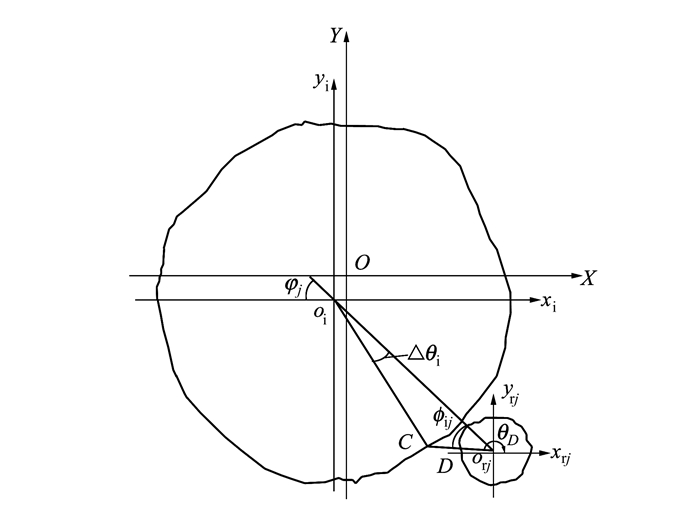
当内圈处于某位置时, 第j个滚子与内圈滚道的几何关系如图 4所示。
|
| 图 4 滚子与内圈滚道几何关系 |
内圈滚道上任一点C与滚子表面上任一点D的距离为
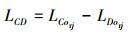
|
(11) |
式中, LCorj为第j个滚子圆心到内圈滚道C点的距离, 由(12)式计算获得; LCorj为第j个滚子自转γ1角后D点的轮廓半径, 由(6)式计算, 其中, D点的位置角可通过几何关系推导获得, 其值与滚子所在象限及D点的位置有关, 当滚子处于第四象限且D点处于直线oiorj下方时, 由(13)式计算。
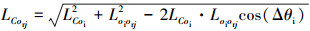
|
(12) |
式中, LCoi为内圈滚道上C点的轮廓半径, 由(4)式计算; Loiorj为内圈圆心到第j个滚子圆心的距离; Δθi为内圈滚道上C点与第j个滚子圆心在圆周方向上的夹角, -arcsin(D/di)≤Δθi≤arcsin(D/di)。
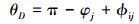
|
(13) |
式中, 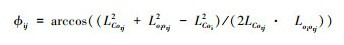
已知内圈圆心坐标和第j个滚子圆心坐标, 任意给定一个Δθi值, 可确定点C的位置角θC, 联立(4)式和(12)式可计算出第j个滚子圆心到点C的距离LCorj; 联立(6)式和(13)式可计算出第j个滚子表面D点的轮廓半径LDorj; 利用(11)式可计算出内圈滚道上任一点C与滚子表面上任一点D的距离LCD; 当Δθi在一定范围内变化时, 在内圈滚道上存在一个C点, 滚子表面上存在一个D点, 使C点到D点的距离LCD最短, 即为滚子表面到内圈滚道的最短距离LCDmin。当LCDmin>ε时, 滚子与内圈滚道分离; 当|LCDmin|<ε时, 滚子与内圈滚道接触; 当LCDmin<-ε时, 滚子与内圈滚道干涉。基于以上计算, 获得了第j个滚子与内圈滚道的位置关系。
同理, 获得轴承下半部每个滚子与内圈滚道的位置关系, 从而获得此位置处内圈滚道的接触状态。以此类推, 可获得每个给定的内圈位置处内圈滚道的接触状态。
1.4 轴承内圈圆心坐标的确定通过上述分析获得了内圈转动α角时不同位置处内圈滚道的接触状态, 在这些内圈位置中仅有一个稳定位置, 此位置具有唯一性, 且此位置处的内圈滚道接触状态应使内圈满足力平衡条件且势能最小。为了从不同内圈位置中判别出内圈的稳定位置, 提出了轴承内圈稳定状态判据。轴承内圈稳定状态判据如下:
1) 滚子与内圈滚道无干涉。由于设定的内圈移动范围比实际范围大, 因此在几何计算中会出现滚子与内圈滚道干涉的情况, 由于这种现象在实际轴承应用中不会发生, 故而当出现这种干涉现象, 即排除此内圈位置作为稳定接触位置的可能;
2) Y轴两侧至少各有一个滚子与内圈滚道接触。对于某个位置对应的内圈滚道接触状态, 没有滚子或只有一个滚子与内圈滚道接触, 或者, 虽有2个及以上滚子与内圈滚道接触, 但所有滚子均位于Y轴一侧, 这些情况下的内圈位置都是不稳定的。只有当Y轴两侧都有滚子与内圈滚道接触时, 内圈才能满足力平衡条件, 此时的内圈处于稳定状态;
3) 滚子接触区中线与Y轴负半轴夹角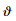
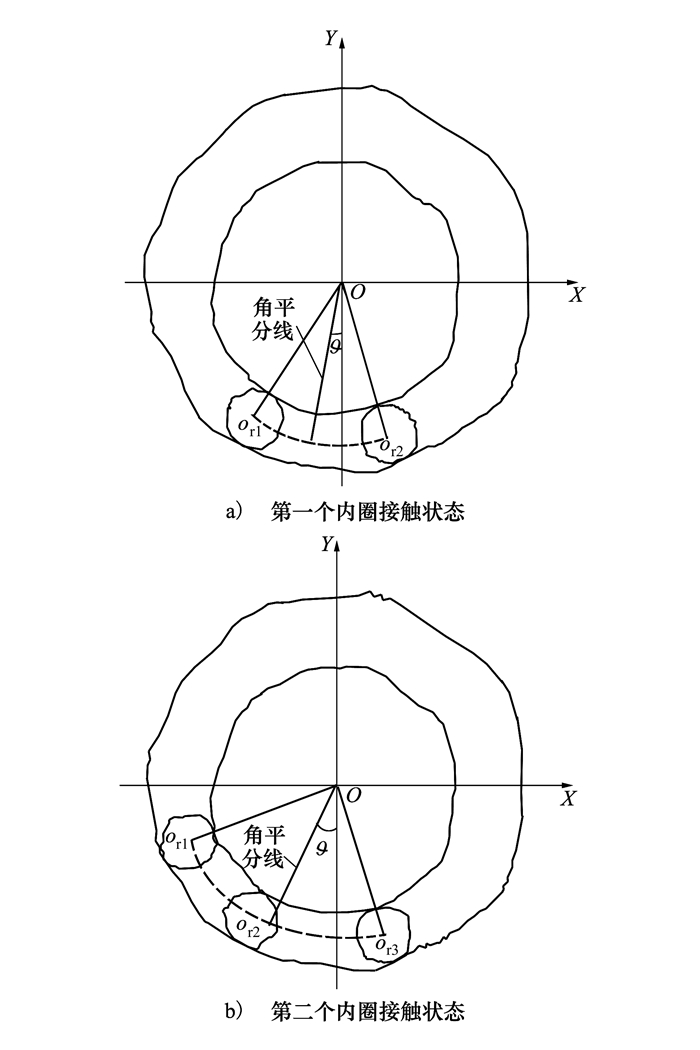
|
| 图 5 内圈稳定状态示意图 |
利用内圈稳定状态判据, 判断若干内圈不同位置对应的滚道接触状态, 获得处于稳定状态的轴承内圈位置, 最终获得内圈旋转任意α角对应的内圈圆心坐标。
2 数值模型的验证为验证本文所提数值模型的正确性, 选取轴承内圈旋转精度数值模型计算的轴承内圈径向跳动与试验结果进行对比验证。试验轴承选用3套NU208型圆柱滚子轴承, 主要参数如表 1所示。依据国标中规定的轴承内圈径向跳动测量原理和方法, 轴承内圈固定于有锥度的高精度心轴上, 通过偏摆仪上2个同轴顶尖与心轴两端锥孔的配合使心轴仅能沿其轴线转动。将千分表探针沿竖直方向压在轴承外圈的中剖面处, 如图 6所示。在测量轴承内圈径向跳动的过程中, 缓慢转动心轴, 通过千分表获得外圈在竖直方向上最大和最小跳动值, 两者之差即为内圈径向跳动。
| 编号 | di/mm | de/mm | D/mm | Z |
| 1 | 49.481 | 71.555 | 10.998~10.999 | 14 |
| 2 | 49.492 | 71.540 | 10.997~10.999 | 14 |
| 3 | 49.499 | 71.545 | 10.997~11 | 14 |

|
| 图 6 轴承内圈径向跳动的测量 |
为了计算NU208圆柱滚子轴承内圈径向跳动, 需要获得轴承内、外圈滚道及滚子直径和圆度误差。利用轴承测量仪获得轴承零件的直径, 如表 1所示; 利用圆度仪获得轴承零件轮廓数据, 并对该数据进行谱分析, 获得各谐波成份的幅值和相位。基于这些参数, 采用傅里叶级数重构轴承零件圆度误差, 并代入(4)~(6)式中, 即可获得轴承零件的轮廓半径。根据轴承结构参数及轴承内圈滚道、外圈滚道和滚子轮廓半径, 利用本文提出的轴承内圈旋转精度数值模型计算轴承内圈径向跳动, 并与试验结果进行对比, 如表 2所示。对比结果表明, 计算结果与试验结果相对误差在13%以下, 试验结果与计算结果有较好的一致性。
基于本文建立的轴承内圈旋转精度数值模型, 在不考虑内圈和外圈滚道几何误差的情况下, 分析了不同尺寸误差滚子的排布方式、滚子表面圆度误差幅值和阶次、不同圆度误差滚子的排布方式、滚子个数对内圈跳动量的影响规律。选用的圆柱滚子轴承为表 1中的第一套轴承。
3.1 不同尺寸误差滚子的排布方式对内圈跳动量的影响当一个或多个滚子存在较大尺寸误差时, 有多种排布方式, 如表 3所示。
| μm | ||
| 类型 | 序号 | 排布方式 |
| 无 | 1 | 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 |
| 一个 滚子 | 2 | 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 |
| 3 | 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 4 | 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 5 | 0.2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 6 | 0.4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 7 | 0.6, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 8 | 0.8, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 2个 滚子 | 9 | 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 |
| 10 | 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 11 | 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 3个 滚子 | 12 | 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 |
| 13 | 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 14 | 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 15 | 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 | |
| 16 | 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0 | |
| 7个 滚子 | 17 | 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0 |
| 18 | 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0 | |
| 所有 滚子 | 19 | 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4 |
| 20 | 0.1, 1.4, 0.2, 1.3, 0.3, 1.2, 0.4, 1.1, 0.5, 1, 0.6, 0.9, 0.7, 0.8 | |
| 21 | 0.1, 0.2, 0.3, 1, 0.4, 1.2, 0.5, 1.1, 0.6, 0.7, 1.3, 1.4, 0.8, 0.9 | |
不同的滚子排布方式对轴承内圈跳动量的影响也不同, 如图 7所示。当只有一个滚子有较大尺寸误差时, 轴承内圈跳动量随着该滚子尺寸误差的增大近似直线上升; 而当多个滚子都具有较大尺寸误差且相邻排布时, 轴承内圈跳动量更进一步显著增大; 当多个具有较大尺寸误差的滚子与具有较小尺寸误差的滚子混合分布时, 轴承内圈跳动量较这些滚子相邻排布时变小, 特别是2种滚子交替排布时轴承内圈跳动量更显著减小; 当对不同尺寸误差的滚子进行装配时, 当按照滚子尺寸误差大小依次排布时, 滚子尺寸误差对轴承内圈跳动量影响最大; 当按照滚子尺寸误差大小交替排布时, 滚子尺寸误差对轴承内圈跳动量影响最小, 且此排布方式下的轴承内圈跳动量仅为递增排布方式下的30%。
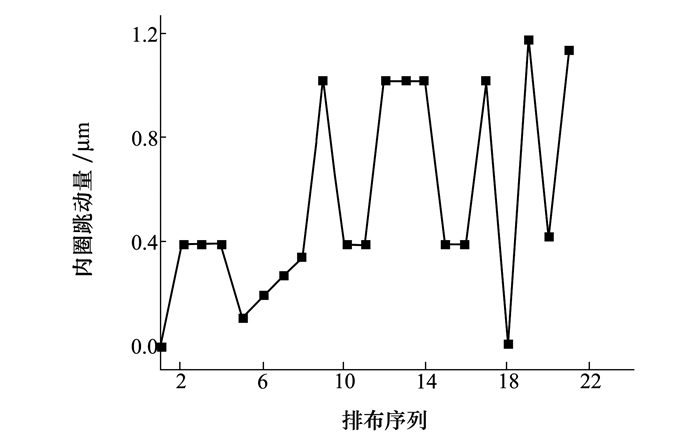
|
| 图 7 不同尺寸误差滚子的排布方式对内圈跳动量的影响 |
图 8给出了滚子个数为14及不同滚子表面圆度误差阶次下, 滚子表面圆度误差幅值对轴承内圈跳动量的影响。当滚子表面圆度误差阶次为偶数时, 随着圆度误差幅值的增大, 轴承内圈跳动量近似呈直线上升, 且其变化趋势随着滚子表面圆度误差偶数阶次的变化而变化; 当滚子表面圆度误差阶次为奇数时, 滚子表面圆度误差幅值对内圈跳动量几乎没有影响。
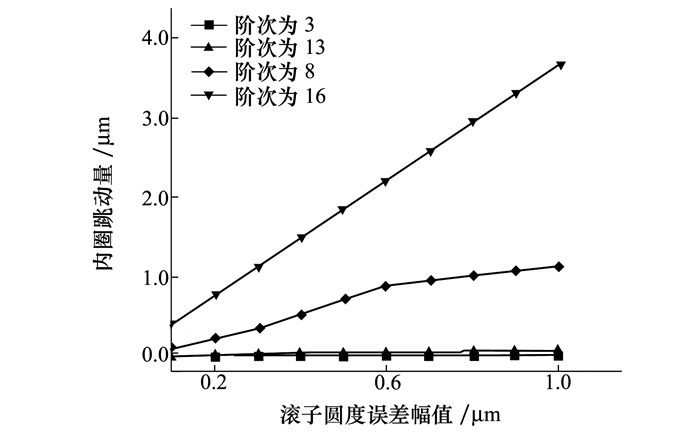
|
| 图 8 滚子表面圆度误差幅值对内圈跳动量的影响 |
图 9给出了滚子表面圆度误差幅值为0.5 μm、不同滚子个数下, 滚子表面圆度误差阶次对轴承内圈跳动量的影响。随着滚子表面圆度误差阶次的变化, 轴承内圈跳动量呈现出剧烈的周期性波动, 其周期取决于滚子个数的奇偶性。当滚子个数为奇数时, 其变化周期对应的圆度误差阶次数等于2倍的滚子个数; 当滚子个数为偶数时, 其变化周期对应的圆度误差阶次数等于滚子个数。当滚子表面圆度误差阶次为奇数时, 轴承内圈跳动量取得极小值, 且其值接近于零; 当滚子表面圆度误差阶次为偶数时, 轴承内圈跳动量取得极大值。由此可以看出, 滚子表面偶数阶圆度误差对内圈跳动量影响很大。
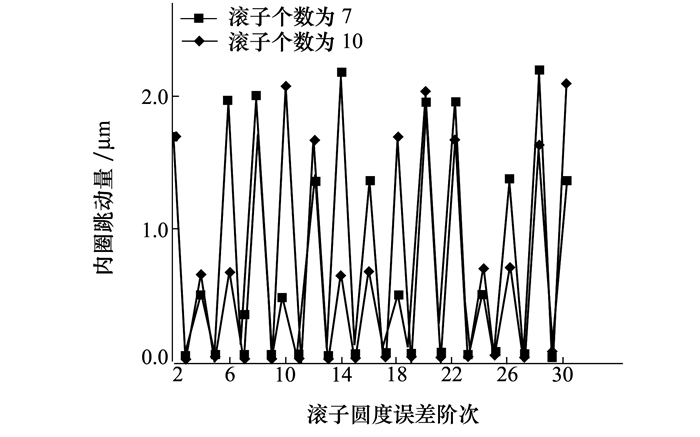
|
| 图 9 滚子表面圆度误差阶次对内圈跳动量的影响 |
为了进一步分析滚子表面圆度误差偶数阶次对轴承内圈跳动量的影响, 图 10给出了滚子圆度误差幅值为0.5 μm、不同滚子个数下, 滚子表面圆度误差偶数阶次对轴承内圈跳动量的影响。
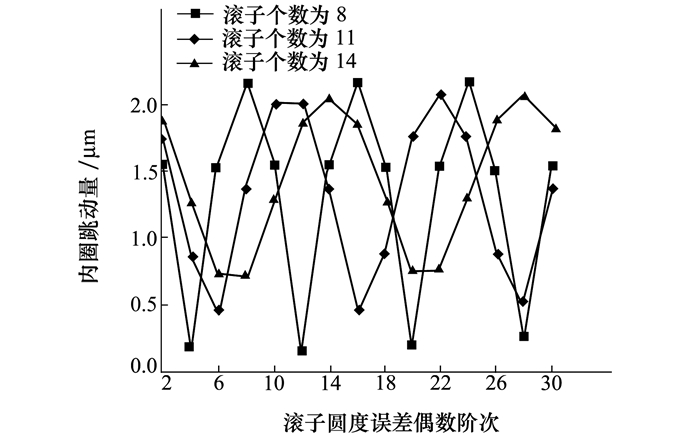
|
| 图 10 滚子表面圆度误差偶数阶次对内圈跳动量的影响 |
从图 10看出, 当滚子个数为偶数时, 滚子表面圆度误差偶数阶次等于nZ(n=1, 2, 3, …), 轴承内圈跳动量取得极大值; 滚子表面圆度误差偶数阶次等于(2n-1)Z/2(Z/2为偶数时)或(2n-1)Z/2±1(Z/2为奇数时), 轴承内圈跳动量取得极小值。当滚子个数为奇数时, 滚子表面圆度误差偶数阶次等于2nZ或(2n-1)Z±1, 轴承内圈跳动量取得极大值; 滚子表面圆度误差偶数阶次等于((2n-1)Z+(-1)((2n-1)Z+1)/2)/2, 轴承内圈跳动量取得极小值。
3.2.3 不同圆度误差滚子的排布方式对内圈跳动量的影响轴承有多个滚子, 每个滚子的圆度误差也不尽相同。为分析具有不同圆度误差的滚子安装顺序对轴承内圈跳动量的影响, 给出了不同圆度误差滚子的排布方式, 如表 4所示。
| 类型 | 序号 | 排布方式 |
| 偶数 阶次 | 1 | 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 |
| 2 | 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6 | |
| 3 | 4, 6, 4, 6, 4, 6, 4, 6, 4, 6, 4, 6 | |
| 4 | 4, 8, 4, 8, 4, 8, 4, 8, 4, 8, 4, 8 | |
| 5 | 4, 10, 4, 10, 4, 10, 4, 10, 4, 10, 4, 10 | |
| 奇数 阶次 | 6 | 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5 |
| 7 | 5, 7, 5, 7, 5, 7, 5, 7, 5, 7, 5, 7 | |
| 8 | 5, 9, 5, 9, 5, 9, 5, 9, 5, 9, 5, 9 | |
| 9 | 5, 11, 5, 11, 5, 11, 5, 11, 5, 11, 5, 11 | |
| 奇偶 交替 | 10 | 4, 5, 4, 5, 4, 5, 4, 5, 4, 5, 4, 5 |
| 11 | 4, 7, 4, 7, 4, 7, 4, 7, 4, 7, 4, 7 | |
| 12 | 4, 9, 4, 9, 4, 9, 4, 9, 4, 9, 4, 9 | |
| 奇奇 偶偶 交替 | 13 | 4, 4, 5, 5, 4, 4, 5, 5, 4, 4, 5, 5 |
| 14 | 4, 4, 7, 7, 4, 4, 7, 7, 4, 4, 7, 7 | |
| 15 | 4, 4, 9, 9, 4, 4, 9, 9, 4, 4, 9, 9 |
图 11为不同的滚子排布方式对轴承内圈跳动量的影响。当具有2种偶数阶次圆度误差的滚子交替排布时, 轴承内圈跳动量随着滚子表面圆度误差偶数阶次的变化而呈现出波动变化的趋势, 与所有滚子具有相同偶数阶次圆度误差的影响相比, 前一种排布方式使轴承内圈跳动量显著增大; 当具有不同奇数阶次圆度误差的滚子相邻排布时, 轴承内圈跳动量几乎不变化; 当具有不同奇数和偶数阶次的滚子以各种顺序排布时, 轴承内圈跳动量均取决于滚子表面偶数阶次的圆度误差, 与滚子表面奇数阶圆度误差无关。在滚子加工过程中, 同一批次的滚子表面圆度误差阶次应具有良好的一致性, 即各滚子表面圆度误差的主要阶次保持一致, 有助于提高轴承旋转精度。
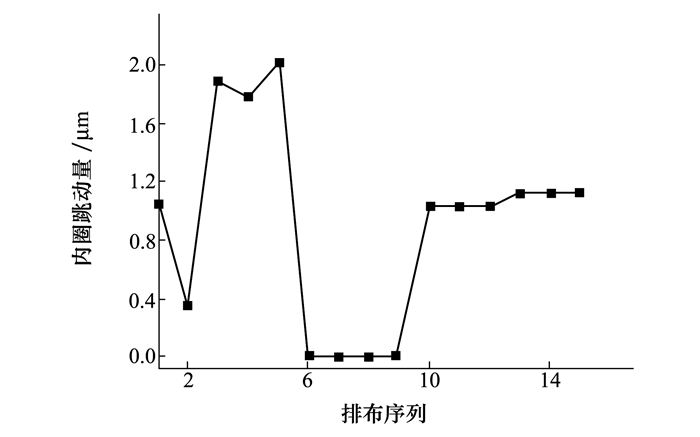
|
| 图 11 不同圆度误差滚子的排布方式对内圈跳动量的影响 |
图 12为不同滚子圆度误差阶次下滚子个数对内圈跳动量的影响。从图中可以看出, 随着滚子个数的增大, 轴承内圈跳动量呈现出非线性变化趋势, 且滚子圆度误差阶次越高其非线性变化趋势越强。当滚子个数和圆度误差阶次满足某种关系时, 内圈跳动量取得极大或极小值。这种关系与3.2节所获得的滚子个数、圆度误差阶次和内圈跳动量三者间的关系是一致的。增加滚子个数并不总使轴承内圈跳动量减小。
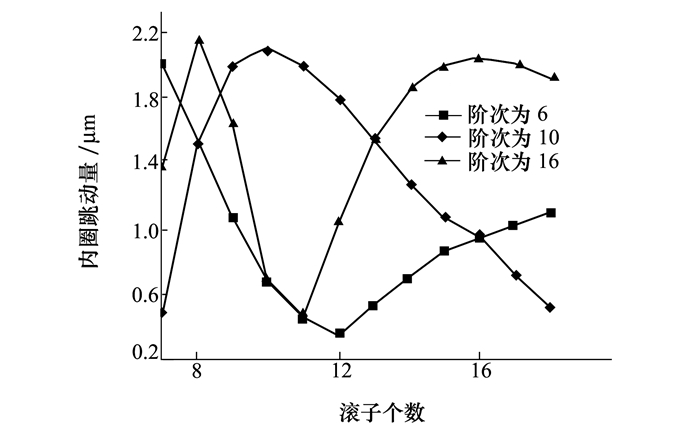
|
| 图 12 滚子个数对内圈跳动量的影响 |
1) 滚子表面偶数阶圆度误差对轴承旋转精度影响显著, 且其影响程度取决于滚子表面圆度误差偶数阶次与滚子个数关系, 当滚子圆度误差偶数阶次等于nZ(Z为偶数)、2nZ或(2n-1)Z±1(Z为奇数)时, 滚子表面圆度误差对轴承旋转精度影响最大; 当滚子圆度误差偶数阶次等于(2n-1)Z/2或(2n-1)Z/2±1(Z为偶数)、((2n-1)Z+ (-1)((2n-1)Z+1)/2)/2(Z为奇数)时, 滚子表面圆度误差对轴承旋转精度影响最小; 而奇数阶圆度误差对轴承旋转精度影响几乎可以忽略。
2) 滚子表面圆度误差对轴承旋转精度的影响呈现出周期性, 其周期取决于滚子个数的奇偶性, 当滚子个数为奇数时, 其变化周期对应的圆度误差阶次数等于2Z; 当滚子个数为偶数时,其变化周期对应的圆度误差阶次数等于Z。
3) 具有不同尺寸误差滚子的排布方式对轴承旋转精度影响显著, 当滚子按照尺寸误差大小交替排布时, 滚子尺寸误误差对轴承旋转精度影响最小; 当滚子按照尺寸误差大小递增排布时, 滚子尺寸误误差对轴承旋转精度影响最大。
4) 滚子表面圆度误差阶次越高, 滚子个数对轴承旋转精度影响越大; 增加滚子个数并不总使轴承旋转精度降低。
| [1] | EBERT F. Fundamentals of Design and Technology of Rolling Element Bearings[J]. Chinese Journal of Aeronautics, 2010, 23(1): 123-136. DOI:10.1016/S1000-9361(09)60196-5 |
| [2] | EBERT F. An Overview of Performance Characteristics, Experiences and Trends of Aerospace Engine Bearings Technologies[J]. Chinese Journal of Aeronautics, 2007, 20(4): 378-384. DOI:10.1016/S1000-9361(07)60058-2 |
| [3] | HARRIS T A. Rolling Bearing Analysis[M]. New York: Taylor & Francis Group, 1999. |
| [4] | TADA S. Three-Dimensional Analysis of Non-Repeatable Runout(NRRO) in Ball Bearing[J]. KOYO Engineering Journal, 2002, 161E: 31-37. |
| [5] |
袁幸, 朱永生, 洪军, 等. 精密球轴承不可重复跳动影响主轴动特性的预测[J]. 吉林大学学报, 2012(2): 382-387.
YUAN Xing, ZHU Yongsheng, HONG Jun, et al. Prediction Model of Spindle Dynamic Characteristics Affected by Non-Repetitive Run-Out of Precision Ball Bearing and Its Application[J]. Journal of Jilin University, 2012(2): 382-387. (in Chinese) |
| [6] | JANG G H, KIM D K, HAN J H. Characterization of NRRO in a HDD Spindle System Due to Ball Bearing Excitation[J]. IEEE Trans on Magnetics, 2001, 37(2): 815-819. DOI:10.1109/20.917622 |
| [7] | NOGUCHI S, ONO K. Reduction of NRRO in Ball Bearings for HDD Spindle Motors[J]. Precision Engineering, 2004, 28(4): 409-418. DOI:10.1016/j.precisioneng.2004.01.005 |
| [8] | NOGUCHI J, HIRUMA K, KAWA H. The Influence of Location of Balls and Ball Diameter Difference in Rolling Bearings on the Non-Repetitive Runout(NRRO) of Retainer Revolution[J]. Precision Engineering, 2005, 29(1): 11-18. |
| [9] | NOGUCHI S, HIRUMA K. Theoretical Analysis of the NRRO of the Components of Retainer Rotation in Consideration of Diameter Difference and Disposition of Balls in a Ball Bearing[J]. Japanses Journal of Tribology, 2003, 48(2): 167-176. |
| [10] | NOGUCHI S, HIRUMA K. Experimental Analysis of the NRRD of the Components of Retainer Rotation in Consideration of Disposition of Balls in a Ball Bearing[J]. Japanses Journal of Tribology, 2003, 48(4): 405-413. |
| [11] | NOGUCHI S, OBINATA S. Influence of the Unequal Orbital Intervals of Balls on the NRRO of Rotational Frequency of the Cage in a Ball Bearing[J]. Japanese Journal of Tribology, 2005, 50(1): 77-85. |
| [12] | NOGUCHI S, NOGUCHI S, TANAKA K, et al. Theoretical Analysis of a Ball Bearing Used in HDD Spindle Motors for Reduction of NRRO[J]. IEEE Trans on Magnetics, 1999, 35(2): 845-850. DOI:10.1109/20.753796 |
| [13] |
马方波, 纪鹏, 李正美, 等. 联合载荷下滚子直径误差对球面滚子轴承力学性能的影响[J]. 中国工程机械学报, 2015, 13(2): 114-119.
MA Fangbo, JI Peng, LI Zhengmei, et al. Impact of Roller Diameter Error on Mechanical Performance of Spherical Roller Bearings under Combined Loading[J]. Chinese Journal of Construction Machinery, 2015, 13(2): 114-119. (in Chinese) |
| [14] | OKAMOTO J, OHMORI T, KITAHARA T. Study on Run-Out of Ball Bearings-Relation Between Unroundness of Race and Locus of Shaft in Rotation[J]. Japanese Journal of Tribology, 2001, 46(7): 578-584. |
| [15] | GUNHEE JANG, SEOⅡG-WEON JEONG. Vibration Analysis of a Rotating System due to the Effect of Ball Bearing Waviness[J]. Journal of Sound and Vibration, 2004, 269(3/4/5): 709-726. |
| [16] | XU L, LI Y. Modeling of a Deep-Groove Ball Bearing with Waviness Defects in Planar Multibody System[J]. Multibody System Dynamics, 2015, 33(3): 229-258. DOI:10.1007/s11044-014-9413-z |
| [17] | KANKAR P K, SHARMA S C, HARSHA S P. Vibration Based Performance Prediction of Ball Bearings Caused by Localized Defects[J]. Nonlinear Dynamics, 2012, 69(3): 847-875. DOI:10.1007/s11071-011-0309-7 |
| [18] | PATEL U A, UPADHYAY S H. Theoretical Model to Predict the Effect of Localized Defect on Dynamic Behavior of Cylindrical Roller Bearing at Inner Race and Outer Race[J]. Journal of Multi-Body Dynamics, 2014, 228(2): 152-171. |
| [19] | WANG F, JING M, YI J, et al. Dynamic Modelling for Vibration Analysis of a Cylindrical Roller Bearing Due to Localized Defects on Raceways[J]. Journal of Multi-Body Dynamics, 2015, 229(1): 39-64. |
| [20] | CHEN G, WANG B, MAO F. Effects of Raceway Roundness and Roller Diameter Errors on Clearance and Runout of a Cylindrical Roller Bearing[J]. Journal of Engineering Tribology, 2013, 227(3): 275-285. |
| [21] | CHEN Guanci, MAO Fanhai, WANG Baokun. Effects of Off-Sized Cylindrical Rollers on the Static Load Distribution in a Cylinder Roller Bearing[J]. Journal of Engineering Tribology, 2012, 226(8): 687-696. |
| [22] | BHATEJA C P, PINE R D. The Rotational Accuracy Characteristics of the Preloaded Hollow Roller[J]. Journal of Lubrication Technology, 1981, 103(1): 6-12. |
| [23] |
余永健, 李济顺, 陈国定, 等. 基于内圈滚道廓形的圆柱滚子轴承旋转精度[J]. 航空动力学报, 2017, 32(1): 155-161.
YU Yongjian, LI Jishun, CHEN Guoding, et al. Rotational Accuracy of the Cylindrical Roller Bearing Based on Inner Raceway Profile[J]. Journal of Aerospace Power, 2017, 32(1): 155-161. (in Chinese) |
| [24] |
宋飞, 李济顺, 刘永刚. 圆柱滚子轴承滚道圆度误差对旋转精度的影响[J]. 轴承, 2011(5): 1-4.
SONG Fei, LI Jishun, LIU Yonggang. Influence of Raceway Roundness Error on Running Accuracy of Cylindrical Roller Bearings[J]. Bearing, 2011(5): 1-4. (in Chinese) |
| [25] |
余永健, 李济顺, 陈国定, 等. 圆柱滚子轴承旋转精度数值计算及试验研究[J]. 机械工程学报, 2016, 52(15): 65-72.
YU Yongjian, LI Jishun, CHEN Guoding, et al. Numerical Calculation and Experimental Research of Rotational Accuracy on Cylindrical Roller Bearing[J]. Journal of Mechanical Engineering, 2016, 52(15): 65-72. (in Chinese) |
| [26] |
史文祥, 李济顺, 刘永刚. 圆柱滚子轴承旋转精度的预测仿真[J]. 机械科学与技术, 2011, 45(4): 72-78.
SHI Wenxiang, LI Jishun, LIU Yonggang. Forecast and Simulation of Rotational Accuracy of Cylindrical Roller Bearing[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 45(11): 72-78. (in Chinese) |
| [27] |
王红军. 滚动轴承测试技术[M]. 北京: 机械工业出版社, 2008.
WANG Hongjun. Testing Technology of the Rolling Bearing[M]. Beijing: China Machine Press, 2008. (in Chinese) |
2. Henan Key Laboratory for Machinery Design and Transmission System, Henan University of Science and Technology, Luoyang 471003, China;
3. State Key Laboratory of Aviation Precision Bearings, Luoyang LYC Bearings Co., Ltd., Luoyang 471003, China


