2. 西安石油大学 陕西省油气井测控技术重点实验室, 陕西 西安 710065
随着世界各国各种竞争力量向海洋的迅速发展, 自主式水下航行器(autonomous underwater vehicle, AUV)凭借着活动范围大、机动性和隐蔽性好、安全、智能等优点,在军事领域被越来越广泛地应用于侦察、探测、目标打击等任务中。通过构建多AUV的集合,在信息共享的前提下,利用作战任务区域内的信息交互,实现多AUV的水下协同对抗,有利于克服单AVU执行任务和作战能力的局限,提高整体作战效能,有效完成各种复杂的军事对抗任务。因此多AUV的水下协同对抗博弈问题引起了全球各国的广泛关注。
协同对抗要求以集合的形式协调行动,并且依据个体所掌握的己方和敌方信息,同时或先后,一次或多次改变各自的行为和策略,以达到己方利益最大化的目的。目前对于协同对抗的研究多以机器人、无人机等为研究对象展开,对其对抗中的任务分配、作战方式、干扰手段等方面进行了大量的研究和探讨。自然进化计算、社会进化计算、生物智能计算、群集智能计算等智能算法也被大量运用于武器分配,协同搜索等问题的研究中来。文献[1]利用博弈理论实现了多机器人系统的无通信任务分配,根据距离信息建立机器人类型的联合概率分布,求解不完全信息动态博弈,有效地提高了通信质量。文献[2]对无人机空战对抗中以固定速度水平飞行的一对一空战机动问题,提出了一种近似动态规划的方法。文献[3]对离散的无人机空战对抗仿真模型用博弈论的方法进行了分析和验证。文献[4]综合考虑了无人机数量、武器配置及地面防御系统等因素,讨论了无人机对地攻击中的战术协同问题,提出了基于Dubins′路径的无人机分组算法。文献[5]分析研究了多机器人巡逻编队和被巡逻对象之间的博弈特性,提出了一种基于博弈论的分布式动态协同方法。文献[6]提出了应用空间链调度的方法解决多机器人任务分配中的协同博弈问题。文献[7]针对无人车集群执行再入体着靶协同监视过程中的集群聚集行为,提出了基于合作博弈的智能集群自主聚集策略。文献[8]针对无人机协同攻击的动态多策略性,以联合生存概率和武器消耗为基础建立了一种多战斗步的空战动态目标分配优化模型。将精英改选机制的的粒子群算法应用到目标分配模型求解纳什均衡点,获取双方的混合策略。
在海战中AUV的协同对抗研究因受制于水下特有的通信能力受限、探测能力受限、位置信息模糊等特点尚处于初级阶段。文献[9]建立了战役层次零和作战动态博弈模型,在不需要其他Agent的完全信息时,给出了Nash均衡的求解方法。对基于Nash-Q的网络信息体系对抗认知决策行为进行了探索和研究。文献[10]在水下对抗方面,对声传感器节点间协作的不同博弈方法进行了探讨,比较了它们在不同度量条件下的性能。随着无人化的飞速发展,战争中以无人武器作为对抗主体的信息化作战已成为趋势,因此对于水下的多AUV博弈对抗问题引起了国内外学者的广泛关注。
本文从博弈对抗的角度,针对海战中AUV协同对抗敌我双方最优策略的选择问题,以多AUV的多次对抗为作战背景,从动态博弈的思想出发,提出了一种考虑敌方策略选择的前提下,寻找己方最优对抗策略的方法,以期实现收益的最大化。该方法通过引入敌方选择策略的评价,以生存概率为指标建立了多战斗步的多AUV动态博弈对抗目标分配模型。根据对前一步对抗后的敌我双方战况评估,在所建立的动态博弈模型的基础上,通过粒子群算法,更加有效准确地获取对抗双方的最优攻击策略,从而更好地模拟实际海战情况,为后续作战的策略选择提供理论依据。
1 多AUV系统博弈对抗的数学描述多AUV系统的博弈模型一般包含2种形式:①纯策略的博弈模型;②混合策略的博弈模型,当混合策略中选取某一种策略的概率为1时,即为纯策略。在实际对抗中,两者均需根据战场动态变化的信息和自主决策信息,确定双方的策略集,建立敌我双方的攻防对抗赢得函数,从而得到博弈双方的支付矩阵。
将对抗中的攻防双方分别看作局中人A和局中人D, 则局中人集合可以表示成为I={A, D}, A(Attack)为己方AUV编队, D(Defend)为敌方的AUV编队, 敌我双方AUV均自身携带数枚武器。A方对D方发动攻击, 以最大概率摧毁D方, 且保证己方生存的最大概率, D方对A方AUV的攻击实施防御和反击, 使己方攻击时造成的损失最小而反击时的收益最大。在双方对抗过程中, 二者的目的都是最大程度歼灭敌人的同时保证己方生存概率的最大化。
假设A方由n个AUV组成的编队集合为{A1, A2, …, An}, D方由m个AUV组成的编队集合为{D1, D2, …, Dm}。A方与D方的对抗状态用xij(i=1, 2…n, j=1, 2…m)表示。xij=1表示A方第i个AUV攻击D方第j个目标, xij=0表示A方第i个AUV放弃攻击处于防御状态。D方发现AUV攻击时, 需要通过对当前的战场态势进行评估, 选择是对发动攻击的AUV实施反击还是通过采用干扰器或释放声诱饵、气幕弹等来进行防御。同理, yji(i=1, 2…n, j=1, 2…m)表示D方的对抗状态, yji=1表示D方第j个攻击单元反击A方第i个目标, yji=0表示D方第j个攻击单元放弃反击而处于防御状态。A、D双方的策略集可以归纳为{攻击且任务分配, 防御}。式中, xij, yji均为二值决策函数, 取0或1, 分别表示防御和攻击2种对抗状态。
2 基于水下目标分配的动态博弈建模 2.1 基于生存概率的水下目标分配由于博弈对抗A、D双方所能采取的对抗策略和对抗过程有限, 基于动态规划的思想, 将一定的单位时间作为基准, 把作战空间和时间离散化, 则可将对抗博弈阶段视为若干个时域离散的子过程。
A、D对抗双方携带的总武器个数分别为QA和QD, 其中QijA为A方第i个AUV分配给D方第j个AUV的武器个数, QjiD为D方第j个AUV分配给A方第i个AUV的武器个数。PAi(k)和PDj(k)分别表示A方第i个AUV和D方第j个AUV在经过第k个战斗步对抗后的生存概率。sijA(k)和sjiD(k)分别表示A、D双方在第k个阶段的武器分配策略, 并且该策略在双方对抗过程中是变化的。pijA(k)和pjiD(k)分别表示在理想环境下, 战斗的第k个阶段, A方第i个AUV毁伤D方第j个AUV的概率和D方第j个AUV毁伤A方第i个AUV的概率。考虑到水下洋流、透明度、跃层、内波等环境因素的影响, 引入环境因素影响因子γ, 其取值范围在0到1之间。
以追求对抗双方生存概率最大为目的进行目标分配策略选择, 建立A、D双方在第k个战斗步的生存概率数学模型PAi(k)和PDj(k)分别为:
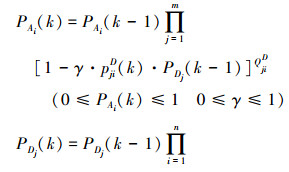
|
(1) |
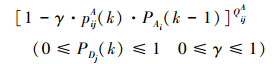
|
(2) |
由于A、D双方在每次对抗过程中发射的武器个数有限且在整个对抗过程中发射的武器总数有限, 所以QijA和QjiD需满足如下约束:
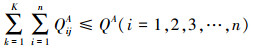
|
(3) |
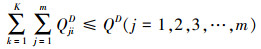
|
(4) |
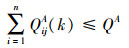
|
(5) |
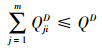
|
(6) |
在对抗全过程结束时, A方和D方的联合生存概率函数分别为
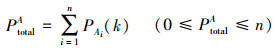
|
(7) |
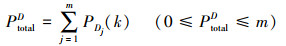
|
(8) |
从以上分析可知, 攻防对抗的目的都是使对方的损失最大, 己方的损失最小, 为了达到这个目的必须合理的对作战目标进行分配。
2.2 基于水下目标分配的动态博弈模型建立在实际对抗中, 战争态势实时变化, 作战双方无法提前获得对方的作战策略信息, 所以很难产生最优目标分配策略。博弈理论的主要特点就是参与各方所采取的行为方案互相依存, 所得到的收益同时依赖于己方和其他参与方所采取的策略, 并且能够在博弈对抗双方信息掌握不完全的条件下寻求最优策略解, 因此用博弈理论的相关知识求解这类问题优势明显。
水下多AUV对抗的目标分配动态博弈模型可以做如下数学表述:记非合作对抗策略问题为G=〈I, S, U〉。其中I为局中人集合, I={A, D}, 代表博弈对抗的A方和D方, 分别称为局中人A和局中人D。S=(sA, sD)为局中人A和局中人D采取的所有策略集合, 其中snA=(s1A, s2A, …sA)为局中人A采取的纯策略集, 纯策略个数为n; sD=(s1D, s2D, …smD)为局中人D采取的纯策略集, 纯策略个数为m。现局中人A和局中人D分别以概率X=(x1, x2, …, xi, …, xn)和Y=(y1, y2, …, yj, …, ym)(xi表示局中人A以xi的概率选择纯策略siA, yj表示局中人D以yj的概率选择纯策略sjD, 且满足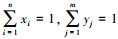
根据双矩阵博弈求解纳什均衡解(X*, Y*)的充要条件[8]Ui·AY*T≤X*UAY*T, X*U·jB≤X*UBY*T, 建立非合作博弈下求解纳什均衡点的适应度函数, 把对纳什均衡点的求取转换成一个优化问题:

|
(9) |
式中, Ui·A为矩阵UA的第i行, U·jB为矩阵UB的第j列, 可以看出使函数f(x, y)为最小值0的混合策略即为所要求得的纳什均衡点。
3 基于粒子群算法的博弈对抗纳什均衡值求解 3.1 算法设计粒子群优化算法是一种模拟鸟群捕食行为的群集智能优化方法。在粒子群优化算法中, 每个粒子代表搜索空间的一个可能解, 种群即为问题潜在解的集合。种群中的每个粒子在解空间中不断搜索进化, 通过目标函数确定每个粒子的适应度函数值, 并以此判断其优劣。通过跟踪自身个体的最优位置和群体的全局最优位置, 利用位置和速度的计算模型实现信息更新, 不断调整自己的飞行速度和方向, 通过迭代搜索最终逼近问题的最优解。
设由NP个粒子构成的种群X=(X1, X2, …, XNp)在D维空间进行搜索, 每个粒子都是待求问题的一个潜在解。设第i个粒子的位置为Xi=(Xi1, Xi2, …, XiD)T, 速度为Vi=(Vi1, Vi2, …, ViD)T, 则根据目标函数可以计算出第i个粒子在位置Xi处的适应度函数值。通过跟踪个体极值Pbesti=(Pi1, Pi2, …, PiD)T和全局极值Gbesti=(Gi1, Gi2, …, GiD)T, 粒子在进化搜索过程中不断更新自身的速度和位置, 向问题最优解逼近。第i个粒子的速度和位置更新公式分别为:
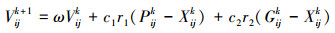
|
(10) |
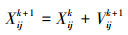
|
(11) |
式中,j=1, 2, …, D, i=1, 2, …, NP, k为当前迭代次数, k=1, 2, …, kmax。ω为惯性权重, 反映了粒子对原来速度的保持情况, c1, c2为正学习因子, r1和r2为在区间[0, 1]内分布的随机数。
本文利用粒子群算法求解水下目标分配问题的纳什均衡, 实际是寻找对抗双方的最优策略组合(X*, Y*), 以对抗双方的混合概率策略组合作为决策变量, 构造粒子。设A方可以采取的策略数为nA, D方可以采取的策略数为nD, 则构造的粒子编码形式为Xi=(Xi1, …, XinA, Yi1, …, YinD), 其中Xi1, …, XinA为A方的混合策略, Yi1, …, YinD为D方的混合策略, 并且有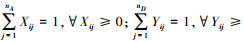
步骤1 根据对抗双方的武器约束、战斗步数等条件, 确定双方对抗策略集合。
步骤2 按照公式(1)、(2)计算对抗双方的收益矩阵UA和UD。
步骤3 以对抗双方的混合策略概率组合构造粒子, 设定粒子群规模为NP, 最大迭代次数为kmax, 误差精度ε。在满足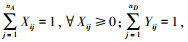
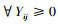
步骤4 根据公式(9), 计算每个粒子的适应度函数值, 找到粒子的个体极值Pbesti和全局极值Gbesti。
步骤5 根据公式(10)~(11)分别对粒子的速度和位置进行更新, 得到新一代粒子; 对当前粒子和其对应的个体最优粒子进行排序, 得到新的个体最优粒子, 将所有的个体最优粒子进行排序得到新的全局最优粒子。
步骤6 判断是否满足迭代结束条件(达到允许误差精度范围或最大迭代次数), 若不满足返回步骤4, 若满足继续下一步。
步骤7 输出全局极值Gbesti, 其位置Xi即为所要找的纳什均衡点。
4 仿真算例为验证本文算法的有效性, 进行如下仿真场景设计:对抗双方A(attack)方和D(defend)方各有2个AUV, 每个AUV携带2枚武器, 进行2个战斗步的攻防对抗。在一个战斗步中每个目标至少分配且最多被分配一个武器, 整个战斗过程中, 每个AUV最多被分配2枚武器。各攻击单元理想情况下的攻击毁伤概率为:P1, 1A=0.9, P1, 2A=0.8, P2, 1A=0.25, P2, 2A=0.15, P1, 1D=0.4, P1, 2D=0.75, P2, 1D=0.5, P2, 2D=0.8。取环境影响因子γ=1。
进行对抗双方策略分析。按(1)~(2)式计算可得A、D博弈对抗双方的价值收益矩阵。在进行k个战斗步的攻防对抗过程中, 设每一个战斗步的一个AUV的最大生存概率上限为1, 则经过k个战斗步后, 一个AUV的生存概率可以看作是其每个战斗步生存概率之和, 则其生存概率最大值上限为k。以A方编队为例, 经过2个战斗步后, 其生存概率最大值上限为2,A方的收益矩UA如表 1所示(因篇幅原因,仅列出部分策略收益)。
| D方策略 | A方策略 | ||||||||||||
| 1 | 2 | 3 | …… | 7 | 8 | 9 | …… | 13 | 14 | 15 | 16 | ||
| 1, 1;1, 1 | 1, 1;1, 2 | 1, 1;2, 1 | …… | 1, 2;2, 1 | 1, 2;2, 2 | 2, 1;1, 1 | …… | 2, 2;1, 1 | 2, 2;1, 2 | 2, 2;2, 1 | 2, 2;2, 2 | ||
| 1 | 1, 1;1, 1 | 1.140 | 1.142 | 1.145 | …… | 1.164 | 1.160 | 1.191 | …… | 1.161 | 1.163 | 1.162 | 1.164 |
| 2 | 1, 1;1, 2 | 0.495 | 0.492 | 0.493 | …… | 0.605 | 0.607 | 1.049 | …… | 1.041 | 1.044 | 1.042 | 1.043 |
| 3 | 1, 1;2, 1 | 1.091 | 1.092 | 1.094 | …… | 1.098 | 1.094 | 0.728 | …… | 0.526 | 0.529 | 0.527 | 0.521 |
| 4 | 1, 1;2, 2 | 0.486 | 0.489 | 0.487 | …… | 0.598 | 0.594 | 0.668 | …… | 0.519 | 0.516 | 0.517 | 0.513 |
| 5 | 1, 2;1, 1 | 0.481 | 0.491 | 0.489 | …… | 0.531 | 0.532 | 0.574 | …… | 0.539 | 0.529 | 0.528 | 0.527 |
| 6 | 1, 2;1, 2 | 0.629 | 0.624 | 0.623 | …… | 0.643 | 0.642 | 0.589 | …… | 0.543 | 0.539 | 0.535 | 0.536 |
| 7 | 1, 2;2, 1 | 0.486 | 0.483 | 0.489 | …… | 0.534 | 0.531 | 0.627 | …… | 0.596 | 0.599 | 0.597 | 0.598 |
| 8 | 1, 2;2, 2 | 0.639 | 0.637 | 0.635 | …… | 0.657 | 0.658 | 0.672 | …… | 0.6435 | 0.648 | 0.646 | 0.647 |
| 9 | 2, 1;1, 1 | 0.493 | 0.494 | 0.497 | …… | 0.529 | 0.526 | 0.568 | …… | 0.529 | 0.527 | 0.525 | 0.524 |
| 10 | 2, 1;1, 2 | 0.534 | 0.535 | 0.533 | …… | 0.5602 | 0.564 | 0.563 | …… | 0.513 | 0.5186 | 0.517 | 0.518 |
| 11 | 2, 1;2, 1 | 0.487 | 0.486 | 0.488 | …… | 0.519 | 0.517 | 0.558 | …… | 0.520 | 0.522 | 0.525 | 0.523 |
| 12 | 2, 1;2, 2 | 0.549 | 0.542 | 0.545 | …… | 0.574 | 0.578 | 0.592 | …… | 0.557 | 0.555 | 0.553 | 0.554 |
| 13 | 2, 2;1, 1 | 0.536 | 0.537 | 0.535 | …… | 0.603 | 0.607 | 0.682 | …… | 0.599 | 0.589 | 0.596 | 0.594 |
| 14 | 2, 2;1, 2 | 0.982 | 0.983 | 0.980 | …… | 0.976 | 0.977 | 0.744 | …… | 0.644 | 0.643 | 0.646 | 0.649 |
| 15 | 2, 2;2, 1 | 0.546 | 0.545 | 0.542 | …… | 0.621 | 0.623 | 0.921 | …… | 0.926 | 0.929 | 0.928 | 0.927 |
| 16 | 2, 2;2, 2 | 1.010 | 1.017 | 1.006 | …… | 1.015 | 1.011 | 1.014 | …… | 1.012 | 1.011 | 1.013 | 1.011 |
以表 1为例对表格含义进行说明。表 1为A、D双方经过2个战斗步后即k=2时A方的生存概率。表中第1行元素为A方所采取策略的策略编号。第2行元素对应A方采取的一个策略, 以第一行策略编号7的(1, 2;2, 1)策略为例, 该策略表示在第1个战斗步k=1时A方AUV1攻击D方AUV1, A方AUV2攻击D方AUV2, 在第二个战斗步k=2时A方AUV1攻击D方AUV2, A方AUV2攻击D方AUV1。同理第1列和第2列分别表示D方采取的策略编号和具体策略。当A方和D方各自选定了策略, 则形成的策略组合对应的值即为A方的收益。
本文采用粒子群算法对建立的水下目标分配动态博弈模型进行仿真验证。设置仿真参数, 权重系数ω=0.729, 学习因子c1=c2=1.4, 种群规模NP=50, 误差精度ε=0.005, 最大迭代次数kmax=100。
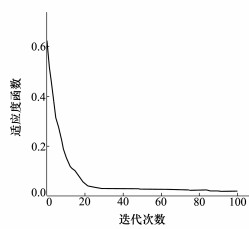
用文中算法计算得到适应度函数值曲线如图 1所示, A、D博弈对抗双方的纳什均衡解如表 2所示。
|
| 图 1 适应度函数曲线 |
| 策略编号 | 策略 | A方最优X* | D方最优Y* |
| 1 | 1, 1;1, 1 | 0 | 0 |
| 2 | 1, 1;1, 2 | 0.789 6 | 0 |
| 3 | 1, 1, 2, 1 | 0 | 0 |
| 4 | 1, 1, 2, 2 | 0 | 0 |
| 5 | 1, 2;1, 1 | 0 | 0 |
| 6 | 1, 2;1, 2 | 0 | 0.176 3 |
| 7 | 1, 2;2, 1 | 0 | 0 |
| 8 | 1, 2;2, 2 | 0.210 4 | 0 |
| 9 | 2, 1;1, 1 | 0 | 0 |
| 10 | 2, 1;1, 2 | 0 | 0 |
| 11 | 2, 1;2, 1 | 0 | 0 |
| 12 | 2, 1;2, 2 | 0 | 0 |
| 13 | 2, 2;1, 1 | 0 | 0 |
| 14 | 2, 2;1, 2 | 0 | 0.826 4 |
| 15 | 2, 2;2, 1 | 0 | 0 |
| 16 | 2, 2;2, 2 | 0 | 0 |
从图 1可以看出适应度函数值曲线在20代内快速收敛, 随着迭代次数增加收敛速度变慢, 最终适应度的值收敛于0.017 46, 得到的双方混合策略如表 2所示。从表 2中可以看出, A方采取的最优混合策略X*为以0.789 6的概率选择策略2, 以0.210 4的概率选择策略8, 若选择纯策略则A更倾向于选择策略2;D方采取的最优混合策略Y*为以0.826 4的概率选择策略14, 以0.176 3的概率选择策略6, 若选择纯策略则D方更倾向于选择策略14。采用表 2中的最优混合策略可以计算得到A方收益X*UAY*T=0.902 8, D方收益X*UBY*T=0.800 2。可以看出A方收益大于D方收益, A方获胜。
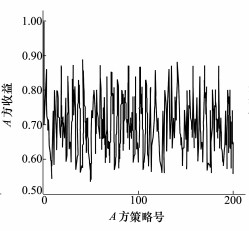
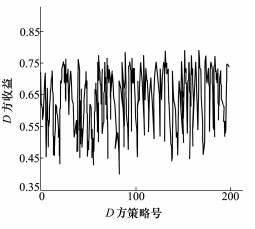
为了验证(X*, Y*)为纳什均衡点, 对A、D两方分别随机生成200组混合策略[X]200×16, [Y]200×16, 计算XUAY*T和X*UBYT的值, 可以得到A方和D方在单方面改变策略时各自的收益, 如图 2、图 3所示。
很明显, 从图 2,3可以看出, 当D方保持策略Y*不变而A单方改变策略时, A方的收益始终小于0.902 8;当A方保持策略X*不变D单方改变策略时, D方的收益始终小于0.800 2, 满足了纳什均衡条件:XUAY*T≤X*UAY*T, X*UBYT≤X*UBY*T。可以看出对抗双方无论哪一方都不能通过单方面策略的改变提高己方的收益, 因此混合策略(X*, Y*)即为要找的纳什均衡, 此时A, D双方的收益分别为(0.902 8, 0.800 2)。
|
| 图 2 A方随机改变混合策略A方的收益 |
|
| 图 3 D方随机改变混合策略D方的收益 |
本文将多自主水下航行器多次对抗的动态目标分配问题与博弈论中的纳什均衡概念相结合,考虑双方生存概率,建立了AUV多战斗回合的动态博弈目标分配模型。
将粒子群算法应用到所建立的动态博弈目标分配模型中去,成功得到了纳什均衡下的双方最优混合策略,验证了所建立模型的正确性和有效性, 对目前信息化海战决策有一定的指导作用。
| [1] | DAI W, LU H, XIAO J, et al. Task Allocation without Communication Based on Incomplete Information Game Theory for Multi-Robot Systems[J]. Journal of Intelligent & Robotic Systems, 2018(1): 1-16. |
| [2] | MCGREW J S, HOW J P, WILLIAM B, et al. Air-Combat Strategy Using Approximate Dynamic Programming[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(5): 1641-1654. DOI:10.2514/1.46815 |
| [3] | POROPUDAS J, VIRTANEN K. Game-Theoretic Validation and Analysis of Air Combat Simulation Models[J]. IEEE Trans on Systems, Man and Cybernetics, Part A:Systems and Humans, 2010, 40(5): 1057-1070. DOI:10.1109/TSMCA.2010.2044997 |
| [4] | SURESH M, GHOSE D. UAV Grouping and Coordination Tactics for Ground Attack Missions[J]. IEEE Trans on Aerospace and Electronic Systems, 2012, 48(1): 673-692. DOI:10.1109/TAES.2012.6129663 |
| [5] | HERNANDEZ E, CERRO J, BARRIENTOS A. Game Theory Models for Multi-Robot Patrolling of Infrastructures[J]. International Journal of Advanced Robotic Systems, 2013, 10(181): 1-9. |
| [6] | TORBJØRN S D, MAJA M, GAURAV S. Sukhatme Multi-Robot Task Allocation through Vacancy Chain Scheduling[J]. Robotics and Autonomous Systems, 2009, 57: 674-687. DOI:10.1016/j.robot.2008.12.001 |
| [7] |
王训, 王兆魁, 张育林. 基于合作博弈的智能集群自主聚集策略[J]. 国防科技大学学报, 2017, 39(2): 146-151.
WANG Xun, WANG Zhaokui, ZHANG Yulin. Strategy about Autonomous Aggregation of Intelligent Swarm Based on Cooperative Game[J]. Journal of National University of Defense Technology, 2017, 39(2): 146-151. (in Chinese) |
| [8] |
王昱, 章卫国, 傅莉, 等. 基于精英改选机制的粒子群算法的空战纳什均衡策略逼近[J]. 控制理论与应用, 2015, 32(7): 857-865.
WANG Yu, ZHANG Weiguo, FU Li, et al. Nash Equilibrium Strategies Approach for Aerial Combat Based on Elite Re-Election Particle Swarm Optimization[J]. Control Theory & Applications, 2015, 32(7): 857-865. (in Chinese) |
| [9] |
闫雪飞, 李新明, 刘东, 等. 基于Nash-Q的网络信息体系对抗仿真技术[J]. 系统工程与电子技术, 2018(1): 217-224.
YAN Xuefei, LI Xinming, LIU Dong, et al. Confrontation Simulation for Network Information System-of-Systems Based on Nash-Q[J]. Systems Engineering and Electronics, 2018(1): 217-224. (in Chinese) |
| [10] | MUHAMMED D, ANISI M H, ZAREEI M, et al. Game Theory-Based Cooperation for Underwater Acoustic Sensor Networks:Taxonomy, Review, Research Challenges and Directions[J]. Sensors, 2018, 18(2): 150-173. DOI:10.3390/s18010150 |
2. Shaanxi Key Laboratory of Measurement and Control Technology for Oil and Gas Well, Xi'an Shiyou University, Xi'an 710065, China


