多阶段系统(phased-mission systems,PMS)广泛存在于航空航天、汽车等大型复杂设备中。大型复杂设备功能的完成往往由一系列阶段任务组成,如地球同步轨道卫星在转移轨道阶段需经历多次变轨阶段,如太阳捕获阶段、地球捕获阶段、地球指示阶段等。PMS各阶段之间属于串联关系,任意阶段任务失败整个系统任务将失败。PMS各阶段任务不同,因此各阶段系统构成、元件配置、任务持续时间也不尽相同,加之阶段内以及阶段间通常存在元件共用即同一个元件可能在阶段内多个位置使用或者在多个阶段被使用,这使得PMS各阶段不是彼此独立存在即存在相关性。PMS各个阶段处于的物理环境通常不同,因此各阶段元件受到的应力水平也不尽相同,即同一元件在各阶段的失效率可能不同,如何求解共用元件在各阶段的可靠度以及如何对PMS进行可靠性建模与求解一直是PMS可靠性领域的研究热点之一。
现有PMS可靠性分析方法可分为3类:静态模型法、动态模型法以及蒙特卡罗仿真方法。静态模型法[1-3]主要有可靠性框图方法、故障树方法、贝叶斯网络方法(Bayesian networks, BN)、二元决策图法、多元决策图法等。静态模型方法假设元件失效具有独立性,但实际系统在阶段内以及阶段间可能存在元件共用,这使得静态分析法受到很大限制。结合阶段代数与二元决策图(binary decision diagram, BDD)的PMS-BDD方法[4]很好地解决了阶段间的相关性以及元件共用问题,但BDD对变量排序有严格要求,不同的变量排序产生的节点规模相差极大,以及PMS-BDD方法难以求取含有多种失效分布类型元件的系统可靠度;贝叶斯网络方法利用节点间的条件概率关系能很好地表示元件在阶段内以及阶段间的共用性,并有成熟BN推理算法可以利用。文献[5-6]将系统任务时间离散后利用离散BN对PMS进行了建模,但随着元件数量以及离散状态数量增加,BN节点的条件概率表规模将呈指数增大[7],且该方法的解只是系统可靠度的近似解。静态方法目前主要集中在共因失效[8]、多模式失效[9]、阶段组合需求[10]等问题的研究。
动态模型法利用元件阶段状态概率从一个阶段映射到后一个阶段来对系统的状态进行分析,通过状态的转移描述系统的变化过程,最后得到任务的可靠概率。基于动态模型分析方法包括Markov模型[11]、Petri网模型(Petri net, PN)[12]。动态方法能考虑阶段内以及阶段间的元件共用性,但随着元件数量增加系统状态规模将呈指数增长即存在组合爆炸问题。
基于大数定理的蒙特卡罗方法[13]为PMS可靠性分析提供了灵活的建模仿真手段,从原理上来说该方法几乎没有限制,缺点是为了获得一定精度必须多次重复仿真,耗时过长。
除去上述方法在PMS可靠性求解中的缺点,绝大多数文献都假设系统元件失效服从指数分布,即不考虑元件的历史损伤作用,这与实际不符。
针对上述问题本文提出基于累积损伤模型的多阶段系统可靠性分析路集组合方法。该方法以BN理论对PMS进行建模,直观的体现了元件的共用性、系统之间的相关性。累积损伤模型的引入,使该方法对PMS可靠性分析更具一般性。算例分析验证了本文方法的正确性。
1 多阶段系统的BN可靠性建模针对PMS难以建模问题,本文采用BN进行系统建模。BN是一个有向无环图,由节点与有向线段以及各个节点的条件概率表组成。节点分为叶节点、中间节点与根节点。叶节点不具有子节点,根节点不具有父节点,每一个节点都有一个条件概率表,表示各个节点在给定父节点取值时各个状态的概率。整个BN表示所有变量的联合分布。
本文将各阶段故障树分别映射成相应的BN,阶段内以及阶段间的共用元件用有向边连接。多阶段系统之间是串联关系,一个阶段失效则系统失效,为此新建一个虚拟数值节点表示整个系统可靠。在映射相应故障树时需遵循以下规则:
1) 增加的虚拟节点置于最后一层,各阶段根节点置于倒数第二层,从故障树顶层到底层顺序映射;
2) 每个中间节点只有1个父节点,2个子节点, 遇到底层有2个以上子节点时需增加中间节点;
3) 节点编号应从BN第一层开始,同一层从左到右依次增大,下层节点数值大于上层节点数值,节点编号不重复;
4) 故障树与门映射成或门,或门映射成与门,并用文字标注。
建成的BN即是将故障树映射为成功树的一张有向网络。
2 系统路集组合方法 2.1 路集组合理论PMS因各阶段属于串联关系且各阶段存在元件共用造成各阶段任务相关,可靠度难以求解。本文基于BN的链式规则以及条件独立性规则推导出求解PMS可靠度的通式,具体过程如下:
设系统由N个阶段组成,每个阶段可靠则系统可靠,单个阶段可靠为事件Si, i∈[1, N], 由多事件同时发生的交运算有
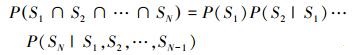
|
(1) |
设阶段i有n个节点, 阶段j有k个节点, 各有x、y个叶节点m个共用元件节点, 由BN的链式规则以及条件独立性规则[14]有
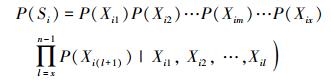
|
(2) |
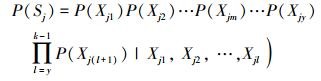
|
(3) |
式中,P(Xju)=P(Xju|Xiu), u∈[1, m], Xix表示阶段i的第x节点, Xjy表示阶段j的第y节点。
设阶段i与j组成串联系统的根节点为M有
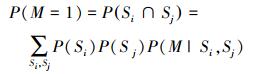
|
(4) |
当M节点可靠, 也就是阶段i与阶段j的系统根节点Si, Sj都可靠时整个系统可靠其条件可靠度概率为P(M=1|Si=1, Sj=1)=1有
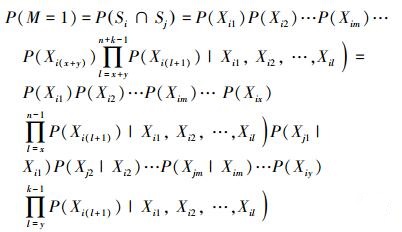
|
(5) |
令
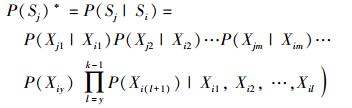
|
为阶段i可靠条件下阶段j可靠的条件可靠度有
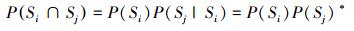
|
(6) |
(6) 式即为任意两阶段串联系统的概率公式。当阶段i, j之间存在其他阶段且与阶段i, j没有共用元件时, 其与阶段i, j条件独立有

|
(7) |
由(6)式和(7)式得出PMS可靠度求解通式为:

|
(8) |
当阶段i与其他阶段存在元件共用时P(Si)*, i∈[1, N]表示条件可靠度, 不存在共用时即是独立可靠度。
对单阶段i, 其可靠度P(Si)等于其最小路集的不交和, 对PMS若阶段之间彼此独立, 则整个PMS的可靠度等于每个阶段的最小路集不交和的积。
当阶段之间存在元件共用, 各阶段最小路集也必存在元件相关, 在(8)式中i也可表示为其最小路集的不交和只是在计算时共用元件的概率为条件概率, 将所有阶段最小路集不交和求积后的所有项即是各个阶段最小不交路集的所有组合, 这些组合有的可以使系统从第1阶段正常工作到最后阶段称之为系统路集组合, 求出所有系统路集组合再求和即是系统可靠度。
2.2 各阶段路集的不交化处理各阶段路集因元件共用造成彼此相关, 不交化处理可以实现路集之间的去相关性。
在BN中分别从各阶段根节点由下至上遍历BN, 寻找最小路集, 遇到与门则该节点上层节点相加, 遇到或门则相乘, 再将所有最小路集按数字顺序从小到大排列, 当遇到串联节点与并联节点相乘时串联节点置于前, 并联节点置于后均需由小到大排列。
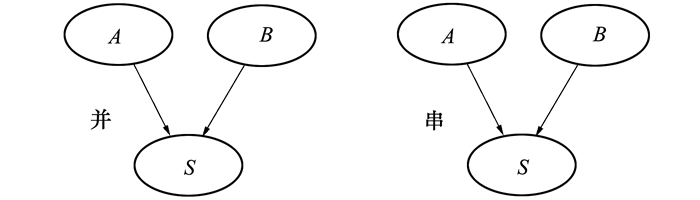
路集不交化:设路集A, B组成BN的2个叶节点, 如图 1所示, 由变量消元法[14]推出路集不交化公式有:
|
| 图 1 串、并联系统贝叶斯网 |
1) 由A, B组合成的并联BN
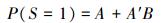
|
(9) |

|
(10) |
2) 由A, B组合成的串联BN
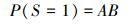
|
(11) |
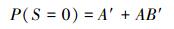
|
(12) |
式中,A, B表示P(A=1), P(B=1)的概率称为显性节点; A′, B′表示P(A=0), P(B=0)的概率, 称为隐性节点。
证明:对由A, B, S组成的并联BN, 其联合分布为P(S, A, B)=P(A)P(B)P(S|A, B), 将等式右侧每项放入桶中如下:
bucket 4: P(S=1|A, B)
bucket 3: P(B)
bucket 2: P(A)
bucket 1:1
将桶1内容代入桶2消去变量S, 再将桶2内容代入桶3消去B, 按此顺序直到消去所有变量如下:
bucket 4: P(S=1|A, B)
bucket 3: P(B) P(S=1|A, B)
bucket 2: P(A)[P(B=1)P(S=1|A, B=1)+P(B=0)P(S=1|A, B=0)]
bucket 1: P(A=1)[P(B=1)P(S=1|A=1, B=1)+P(B=0)P(S=1|A=1, B=0)]+P(A=0)[P(B=1)P(S=1|A=0, B=1)+P(B=0)P(S=1|A=0, B=0)]
根据并联节点S的条件概率表关系:
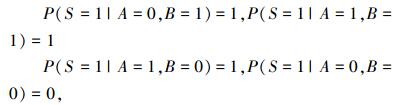
|
对桶1内容化简有
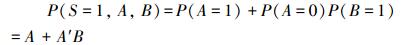
|
其他公式可以按此得证。设有L个经排序的最小路集, 将前L-1个组合在一起作为复合节点A, 第L个作为B, 按公式(9)~(12)进行不交化, 反复利用此公式, 直到每项只含唯一使系统正常工作或失效的节点组合, 即得到所有不交化后的路集。
2.3 路集规模缩减及组合规则系统路集组合前采用阶段内以及阶段间共用元件条件概率关系可以缩减路集规模, 减少计算量。
阶段内共用元件条件概率关系为:

|
(13) |
Xix, Xiy表示阶段i内共用元件的节点号x, y, 即阶段i内共用元件相关节点Xix, Xiy一个失效则所有相关节点失效, 一个可靠则所有相关节点都可靠。
利用(13)式对各阶段最小不交路集数量进行缩减, 即去掉同时含有共用元件显性与隐性节点的路集项。阶段间条件概率关系为:

|
(14) |
式中,Xix, Xjy表示阶段i与阶段j的共用元件的节点号x, y, 即当共用元件在阶段i失效, 在阶段j一定失效。
化简后的路集再利用阶段间条件概率关系从阶段1到最后阶段顺序组合, 组合时按如下2种规则处理共用元件:
1) 若当前阶段某路集项含有的共用元件失效, 则在以后阶段将含有该元件共用节点号且为显性的路集项去掉后再组合;
2) 若当前阶段某路集项含有的共用元件失效, 则在以后阶段将含有该元件共用节点号且为隐性的路集项中的相关隐性节点去掉后再组合。
对组合后的路集项, 若共用元件节点出现在阶段i且为显性, 表示该元件成功工作到阶段i, 若为隐性表示该元件成功工作到阶段i-1且在阶段i失效。
3 元件各阶段可靠度共用元件在PMS各阶段失效率以及工作时间不尽相等, 求解元件各阶段可靠度时需考虑各阶段历史损伤对元件寿命的影响。
3.1 元件各阶段条件寿命分布设元件x在阶段i可靠为事件Sxi, 不同阶段的同一共用元件在时间上属于串联系统, 根据BN链规则以及条件独立性规则, 元件在阶段i的状态只与阶段i-1有关, 元件在阶段i可靠的概率为
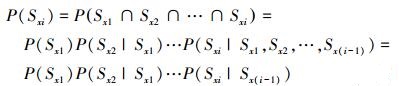
|
(15) |
失效的概率为
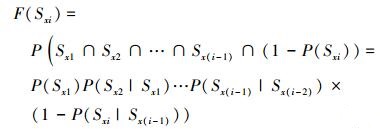
|
(16) |
若求得元件各阶段在上阶段可靠条件下的条件剩余寿命分布既可得元件在各阶段的可靠度。
3.2 元件累积损伤模型元件正常工作到阶段i的剩余寿命分布, 需考虑元件之前阶段工作的累积损伤, Nelson提出元件累积损伤模型(cumulative exposure, CE) [15], 其假定产品的剩余寿命仅依赖于当时已积累失效的部分和当时的应力水平, 而与积累方式无关, 即假定元件在阶段i-1以应力λi-1工作ti-1时间与在阶段i以应力λi工作等效时间ti*造成的不可靠度相等, 阶段i的分布为从等效时间ti*开始, ti*之前的是累积失效部分。由文献[16]可知, 元件在任意阶段的累积失效分布Foi(t)为
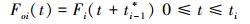
|
(17) |
其中等效时间ti-1*为Fi(ti-1*)=Fi-1(ti-1+ti-2*)的解, ti为阶段i的持续时间, Fi()为元件以失效率λi工作时的分布。
元件在阶段i-1可靠条件下阶段i的条件寿命分布Foi|o(i-1)(t), 根据条件概率贝叶斯公式有
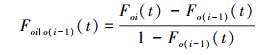
|
(18) |
条件可靠度为:
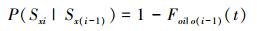
|
(19) |
电气元件失效常服从指数分布, 其各阶段条件寿命分布由(17)式得:
阶段1:Fo1(t)=F1(t)=e-λ1t, 0≤t≤t1
阶段2:
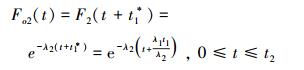
|
式中,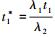
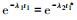
同理可得任意阶段的累积失效分布为
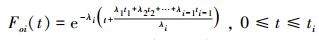
|
(20) |
由(18)式得各阶段条件概率分布为
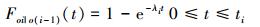
|
(21) |
由(15)式得元件任意阶段的可靠度为

|
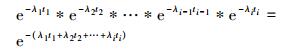
|
(22) |
对机械元件其寿命分布常假设为威布尔分布其各阶段条件寿命分布仍可使用此方法进行计算。
4 算例分析地球同步轨道卫星发射后在转移轨道段需经历多次变轨, 可分为太阳捕获段、地球捕获段、地球指示段、远地点点火准备段、远地点点火段, 以前3阶段的控制系统为例进行建模并求解各阶段可靠度。本文为计算方便对各阶段控制系统结构做了适当简化。
1) 故障树及贝叶斯网建立
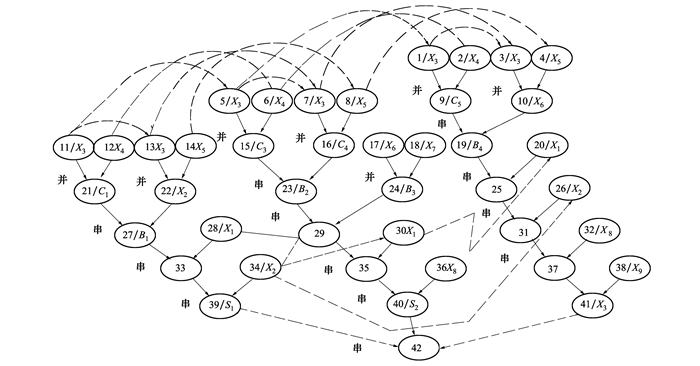
某地球同步轨道卫星控制系统3阶段故障树如图 2所示, 映射成的贝叶斯网如图 3所示。

|
| 图 2 某同步轨道卫星控制系统3阶段故障树 |
|
| 图 3 某同步轨道卫星控制系统3阶段贝叶斯网 |
2) 最小不交路集求解
阶段1最小路集:28×34×(11×13), 28×34×(11×14), 28×34×(12×13), 28×34×(12×14)。
3) 不交化处理
利用(9)~(12)式对阶段1路集做不交化处理有

|
4) 阶段内路集缩减
阶段内存在共用元件节点11与13, 由阶段内共用元件条件概率关系(13)化简有

|
同理可得其余阶段的最小不交路集:
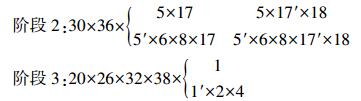
|
5) 系统路集组合
阶段1不存在路集组合, 系统路集为阶段1的最小不交路集D1。
阶段2系统路集:阶段2与阶段1存在元件共用按路集组合规则D2为

|
其中A=30×34×36。
阶段3系统路集:阶段3与阶段1、2存在元件共用, 按路集组合方法D3为
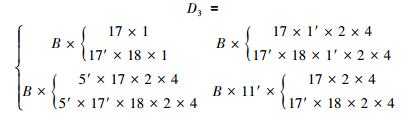
|
其中B=20×26×32×38×36。
6) 系统各阶段可靠度求解
各阶段持续时间t1=50 min, t2=600 min, t3=40 min, 各阶段元件寿命服从指数分布, 失效率如表 1所示。
| 代号 | 失效率/ (10-6·min-1) |
||
| 阶段1 | 阶段2 | 阶段3 | |
| X1 | 3 | 2 | 3 |
| X2 | 2 | 0 | 10 |
| X3 | 10 | 2 | 10 |
| X4 | 10 | 2 | 10 |
| X5 | 10 | 2 | 10 |
| X6 | 0 | 2.5 | 0 |
| X7 | 0 | 2.5 | 0 |
| X8 | 0 | 2 | 3 |
| X9 | 0 | 0 | 3 |
将各元件失效率带入(22)式得各元件在各阶段末失效的概率, 如表 2所示。
| 元件 | 时间/min | ||
| 50 | 600 | 40 | |
| X1 | 0.000 145 | 0.001 349 | 0.001 469 |
| X2 | 0.000 010 | 0 | 0.000 500 |
| X3 | 0.000 500 | 0.001 699 | 0.002 098 |
| X4 | 0.000 500 | 0.001 699 | 0.002 098 |
| X5 | 0.000 500 | 0.001 699 | 0.002 098 |
| X6 | 0 | 0.001 499 | 0 |
| X7 | 0 | 0.001 499 | 0 |
| X8 | 0 | 0.001 199 | 0.001 319 |
| X9 | 0 | 0 | 0.000 120 |
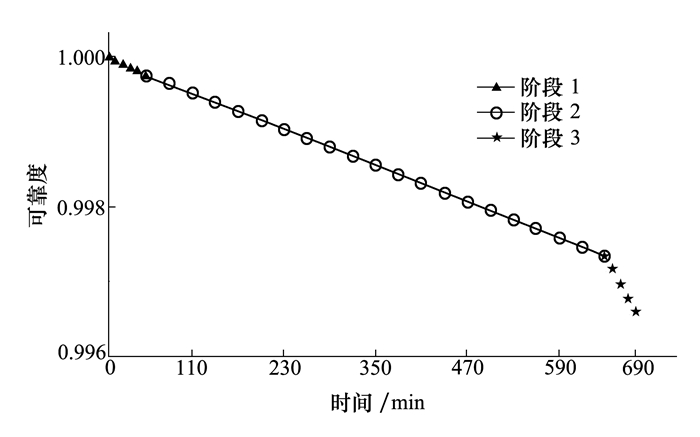
将表 2元件各阶段失效概率带入系统路集D1, D2, D3中既可求得系统处于各阶段末的可靠度。系统可靠度变化如图 4所示, 部分时刻可靠度见表 3。
|
| 图 4 某同步轨道卫星控制系统3阶段可靠度 |
| 时刻/min | 0 | 30 | 50 | 290 | 650 | 670 | 690 |
| 概率 | 1 | 0.999 850 | 0.999 750 | 0.998 788 | 0.997 346 | 0.996 965 | 0.996 584 |
7) PMS-BDD方法求解
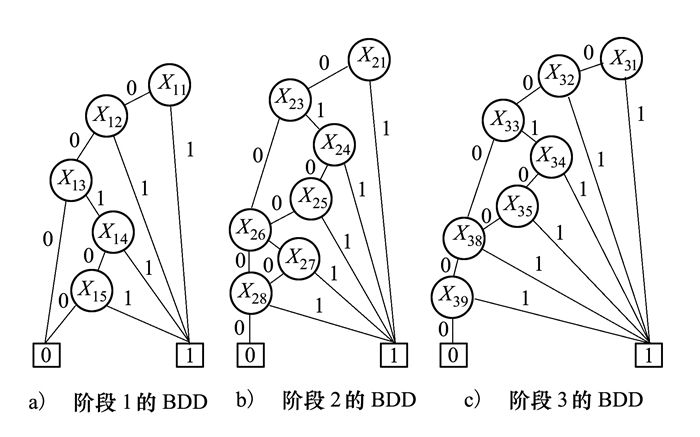
将各阶段故障树转化为相应BDD如图 5所示, 采用向后排序规则, 变量顺序为X31 < X21 < X11 < X32 < X22 < X12 < X33 < X23 < X13 < X34 X24 < X14 < X35 < X25 < X15 < X36 < X26 < X16 < X37 < X27 < X17 < X38 < X28 < X18 < X39 < X29 < X19, 其中Xij表示阶段i的j元件。
|
| 图 5 控制系统各阶段的BDD |
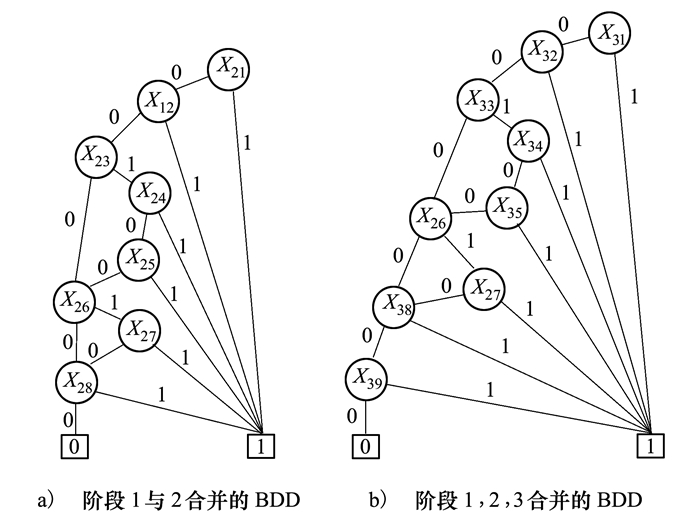
利用阶段代数与向后BDD阶段合并规则[4]将3个阶段的BDD合并为系统BDD, 即先将阶段1的BDD与阶段2的BDD合并再与阶段3的合并, 如图 6所示。
|
| 图 6 阶段合并的BDD |
顶节点到0节点的所有路径即是该阶段的不交路集, 对所有路集求和即是系统在该阶段的可靠度。
求解系统处于阶段2的可靠度, 对应的是阶段1与阶段2合并的BDD, 有4条路径:X21X12X23X26X28, X21X12X′23X24X25X26X28, X21X12X23X′26 X27X28, X21X12X′23X24X25X′26X27X28。X′ij表示j元件在阶段i失效的概率。将表 2元件对应失效概率带入再求和即是系统处于阶段2的可靠度, 同理可得系统部分时刻可靠度如表 3所示, 可见采用PMS-BDD方法与本文方法计算出的表 3数值是一致的。
5 结论1) 本文针对多阶段系统因阶段任务相关、元件共用造成的系统可靠性难以建模与求解问题,提出了基于累积损伤模型的多阶段系统路集组合方法,该方法直接对各阶段不交化后的路集进行组合求和,没有PMS-BDD方法对变量排序的严格限制以及传统BN方法因阶段状态离散过多造成的条件概率表规模大、计算量大问题。且该方法不限制元件的寿命分布类型,有更广的适用性;
2) 针对多阶段共用元件在各阶段工作时长、失效率不同,元件各阶段可靠度难以求取问题,本文考虑元件历史损伤作用,利用元件累积损伤模型,获得元件各阶段条件寿命分布,解决了共用元件在各阶段的可靠度求解问题;
3) 针对路集相关,利用由BN变量消元法推导出的不交化公式实现了路集去相关性。针对路集规模过大问题,利用共用元件的条件概率关系,缩减了路集规模,减小了计算量;
4) 算例分析表明本文方法与PMS-BDD方法计算结果一致,验证了本文方法的正确性。
本文所做的工作,为后续PMS结构优化,以及维修保障性优化工作奠定了理论基础。
| [1] |
陈光宇, 张小民, 唐小我. 基于分离BDD的通用多阶段任务系统可靠性分析[J]. 系统工程理论与实践, 2013, 33(5): 1240-1246.
Chen Guangyu, Zhang Xiaomin, Tang Xiaowo. Analysis of Generalized of Phased-Mission Systems Reliability Based on Separable Binary DecisionDiagram[J]. System Engineering-Theory &Practice, 2013, 33(5): 1240-1246. (in Chinese) DOI:10.3969/j.issn.1000-6788.2013.05.019 |
| [2] | Mo Y C, Liu X, Amari S V. A Multiple-Valued Decision Diagram Based Method for Efficient Reliability Analysis of Non-Repairable Phased-Mission Systems[J]. IEEE Trans on Reliability, 2014, 63(1): 320-330. DOI:10.1109/TR.2014.2299497 |
| [3] | Meng L. Binary Decision Diagram Model for Reliability Analysis of Phased Mission System[J]. Journal of National University of Defense Technology, 2017, 39(2): 184-192. |
| [4] | Zang X, Sun H, Trivedi K S. A BDD-Based Algorithm for Reliability Analysis of Phased-Mission Systems[J]. Reliability Engineering & System Safety, 1999, 66(2): 157-170. |
| [5] | Fan D, Wang Z, Liu L, et al. A Modified GO-FLOW Methodology with Common Cause Failure Based on Discrete Time Bayesian Network[J]. Nuclear Engineering & Design, 2016, 305: 476-488. |
| [6] | Li X T, Tao L M, Jia M A. Bayesian Networks Approach for Event Tree Time-dependency Analysis on Phased-Mission System[J]. Eksploatacja i Niezawodnosc-Maintenance and Reliability, 2015, 17(2): 273-281. DOI:10.17531/ein.2015.2.15 |
| [7] |
王瑶, 孙秦. 一种解决组合爆炸问题的三态故障贝叶斯网络[J]. 西北工业大学学报, 2014, 32(6): 857-864.
Wang Yao, Sun Qin. A Three-State Faulty Bayesian Network for Solving Combinational Explosion Problem[J]. Journal of Northwestern Polytechnical University, 2014, 32(6): 857-864. (in Chinese) DOI:10.3969/j.issn.1000-2758.2014.06.004 |
| [8] | Wang C N, Liu X, Levitin G. Probabilistic Common Cause Failures in Phased-Mission Systems[J]. Reliability Engineering & System Safety, 2015, 144: 53-60. |
| [9] | Mo Y C, Liu X, Duang J B. MDD-Based Method for Efficient Analysis on Phased-Mission Systems with Multimode Failures[J]. IEEE Trans on Systems Man & Cybernetics Systems, 2014, 44(6): 757-769. |
| [10] | Lu J M, Wu X Y. Reliability Evaluation of Generalized Phased-Mission Systems with Repairable Components[J]. Reliability Engineering & System Safety, 2014, 121: 136-145. |
| [11] |
闫华, 王魁, 刘子林, 等. 基于Markov方法的多阶段任务系统可靠性分析综述[J]. 兵器装备工程学报, 2016, 37(6): 92-96.
Yan Hua, Wang Kui, Liu Zilin, et al. Reliability Analysis of Phased-Mission System Using Markov Approach[J]. Journal of Ordnance Equipment Engineering, 2016, 37(6): 92-96. (in Chinese) DOI:10.11809/scbgxb2016.06.022 |
| [12] | Wu X Y, Wu X Y. Extended Object-Oriented Petri Net Model for Mission Reliability Simulation of Repairable PMS with Common Cause Failures[J]. Reliability Engineering & System Safety, 2015, 136: 109-119. |
| [13] | Siddiqui M, Butt S, Gilani O, et al. Optimizing Availability of a Framework in Series Configuration Utilizing Markov Model and Monte Carlo Simulation Techniques[J]. Symmetry, 2017, 9(7): 96. DOI:10.3390/sym9070096 |
| [14] |
张连文, 郭海鹏. 贝叶斯网引论[M]. 北京: 科学出版社, 2006.
Zhang Lianwen, Guo Haipeng. Bayesian Network Introduction[M]. Beijing: Science Press, 2006. (in Chinese) |
| [15] | Nelson W. Accelerated Life Testing - Step-Stress Models and Data Analyses[J]. IEEE Trans on Reliability, 1980, R-29(2): 103-108. DOI:10.1109/TR.1980.5220742 |


