作为图数据之上一类经典的组合优化问题, 最大流问题寻找通过一个流通网络的最大流量, 是网络流理论体系中重要的研究领域[1]。最大流可辅助求解一些重要的基础理论问题, 如双边匹配等线性规划问题, 以及一些重要的应用问题, 如网络规划[2], 网络和信息安全[3]和各类复杂系统中的资源调度[4]等。经典的最大流算法主要包括增广路[5]和预流推进[6]2种方法, 并在2种方法基础上衍生出了很多变种以降低计算复杂度。已知最大流加速方法包括针对有向平面图的快速算法[7], 针对计算机视觉图数据的快速计算方法[8], 以及基于线性代数或电路流的最大流近似计算方法等[9-10]。但随着各行业数据呈爆炸性增长, 传统加速方法已无法应对大规模图上的最大流问题。针对大规模图中最大流加速, 已有方法主要集中在图缩减和并行计算2个方面:
1) 图缩减思路:通过化简原始网络, 降低问题规模并减少后续重复计算。如针对单源单汇最大流问题, 文献[11]提出基于图缩减机制的两阶段最大流方法, 针对几种局部特殊拓扑结构, 将满足给定代数关系的子图缩为节点, 在简化的图上进行快速计算。文献[12]通过多次最大流计算, 构建原始图的最小割树, 以丢失路径信息的代价, 快速求解任意2个节点之间的最大流值。文献[13-14]检测满足缩减标准的网络社区结构, 将其压缩为一点, 在简化的图上获取最大流近似解。文献[15]寻找合并后不影响外部最大流的节点对, 通过多次迭代合并图中的节点对缩小图的规模。文献[16]利用商空间理论建立问题求解的保真和保假原理, 将图中所有节点对之间最大流计算量从n(n-1)/2次降低为n-1次左右。
2) 并行计算思路:基于底层的多种并行架构加速求解过程。早期工作主要集中在实现多处理器环境中的并行算法[17-18]。随着云计算技术的发展, 出现了基于多种通用和专用并行计算模型的加速方法。其中, 文献[19]实现了基于Spark框架的Edmonds-Karp增广路算法, 在算法各步骤采取不同计算模型, 利用框架中内置的pregel和mapreduce等多种计算接口提升算法并行度。文献[20]针对包含上亿节点和数十亿条边的社交网络数据, 在算法和mapreduce框架层进行跨层优化, 将最大流计算时间缩短至10分钟左右。
已有工作中从多个角度对最大流问题进行了探讨, 但仍存在一些问题:①图缩减和并行计算2种加速思路并未充分融合, 基于单个思路的加速效果受限; ②未考虑常见的单个图中多次最大流求解场景, 多次计算间存在大量冗余工作; ③图缩减方法需要涉及出入度和边容量等多个条件, 计算复杂度偏高, 甚至会抵消并行计算加速效果。针对上述问题, 我们尝试利用双连通分量构建覆盖图, 提出了稀疏大图中基于双连通分量覆盖图(BCR:bi-connected component overlay)的并行加速方法。对原始图中任意两点间的最大流问题, 基于覆盖图分解成多个子图内最大流计算问题, 并行求解这些子问题。覆盖图仅涉及连接关系, 对局部拓扑结构没有任何要求, 计算复杂度较低。在基准网络拓扑上的实验结果表明, 算法可显著缩短计算时间, 大幅提升求解效率。
1 模型 1.1 试验方法算法主要处理无向图中的最大流问题, 首先引入连通分量和双连通分量的定义。
定义1 连通分量:在无向图中, 若顶点1和顶点2之间存在路径, 则称顶点1和2连通。若某个子图中任意2个顶点之间都连通, 则称该图为连通图, 其中极大连通子图称为连通分量。
定义2 双连通分量:若任意图中任意2点至少存在2条不存在重复点的路径, 则称该图为双连通图; 对一个无向图, 双连通的极大子图称为双连通分量。
图 1示例中, 左侧虚线包含的子图为双连通分量中。双连通分量和割点有紧密关系, 下面引入割点和双连通分量界点的定义。

|
| 图 1 算法模型图 |
定义3 割点:如在图G中去掉一个顶点, 并同时去掉与该顶点相关联的所有边后, 该图的连通分量数增加, 则称该顶点为图G的割点。
定义4 双连通分量的界点:若某连通分量中节点和外部节点存在边, 称该节点为双连通分量的界点。
割点的示例见图 1中左侧黑色节点, 其中节点8和11也是界点。双连通分量和割点存在如下关系:
引理1 连通图G的某个双连通分量所有界点必然是割点。
证明 设双连通分量为vU, 则有:
1) 若只有一个界点a, 则去除a后, vU和外部不相连, a即为割点。
2) 假设有>=2个界点, 且界点b不是割点。设界点b和外部节点b2相连, 则对于vU中任何一个节点a, 存在路径b2→b→a; 因b不是割点, 则去除b后, b2和节点a间仍存在路径, 设该路径上最早访问到的vU内节点是界点c且有c≠b, 则节点b2到c存在b2→b→c和b2→c 2条路径; 因路径b→c存在只通过vU内节点的路径, 而b2→c不通过任何vU内节点, 即b2到c存在2条路径无重复节点的路径。
3) 因为c和a均为vU内节点, 存在2条无重复节点路径, 进而b2和内部任何节点a, 都存在b2→b→c→a和b2→c→a 2条无重复节点路径, 即包含vU和b2的分量也是双连通分量, 这和vU是双连通极大子图相矛盾。
4) 由于上述证明并未对界点b外的任何其他节点的性质做出假设, 即证明任何一个界点如是割点都会导出矛盾, 可得出在存在>=2个界点情况下, 每个界点都必须是割点。
5) 根据前述证明, 对于存在>=1个界点情况下, 每个界点必然是割点, 证毕。
由引理1可知, 在一个连通图中, 所有双连通分量必然通过割点与外部相连。
引理2 若在原图G的一个连通子图中, 每个界点在分量外的邻居节点只能通过该界点连到连通分量内节点, 且该连通子图中没有割点, 则该连通子图为双连通分量。
证明 取原始图G中任意2个节点及之间的边构成一个小的特殊的双连通图vU, 对vU中节点a在分量外的邻居b, 只要b不通过a也能连到vU内节点, 即b能通过第二个界点a2连到vU内, 则b至少能连到2个不同的界点, 可知对vU内任意节点c, 节点b都有2条无重复节点路径b→a→c和b→a2→c, 因此b也能加入到vU中并组成更大的双连通图。因此, 直到每一个界点在双连通图外邻居只能通过该界点连到连通图内, 这种扩张过程才能停住, 此时获得的是极大双连通图, 即双连通分量。证毕。
基于引理2, 可先找到所有割点, 识别被割点分隔的并以割点为界点的连通分量, 保证分量外邻居节点只能通过界点连到分量内, 即得到双连通分量, 在获取所有双连通分量过程中, 可构建双连通分量覆盖图, 定义如下:
定义5 双连通分量覆盖图:设原始图G对应的双连通分量覆盖图为G′, 对原始图G中每个双连通分量, 在G'中对应一个类型为U的节点; 其每个割点, 在G′中对应一个类型为W的节点vW, 若割点v属于某个双连通分量, 则在该双连通分量在图G′中的U类节点和vW间建立一条边; 对原图中与割点v不属于同一个双连通分量的所有邻居节点, 用他们对应的G′中节点分别和v建立一条边。
图 1中右侧即为双连通覆盖图。关于双连通分量覆盖图G′的拓扑结构, 给出下述定理:
定理3 双连通分量覆盖图G′是树形拓扑。
证明 反证。因不存在环路的图即为树, 假设双连通分量覆盖图G′中存在环路, 依据环路定义, 环路中任意2个节点在G′中存在无重复点的>=2条路径, 即G′中环路上的类型为W的节点对应的原图G中任意两个节点也存在无重复点的>=2条路径, 即G′中环路上的点所对应的点在原图G中属于同一个双连通分量, 而根据生成规则, 同一个双连通分量中所有非割点对应一个U类节点, 每个割点对应的W节点和该U类节点间存在一条边, 同属于一个U类节点的这些W节点之间不会存在边, 即G′中这些节点只会组成局部星形结构, 这和组成环路相矛盾。证毕。
基于定理3, 我们也把双连通分量覆盖图G′写为双连通分量覆盖树T′。
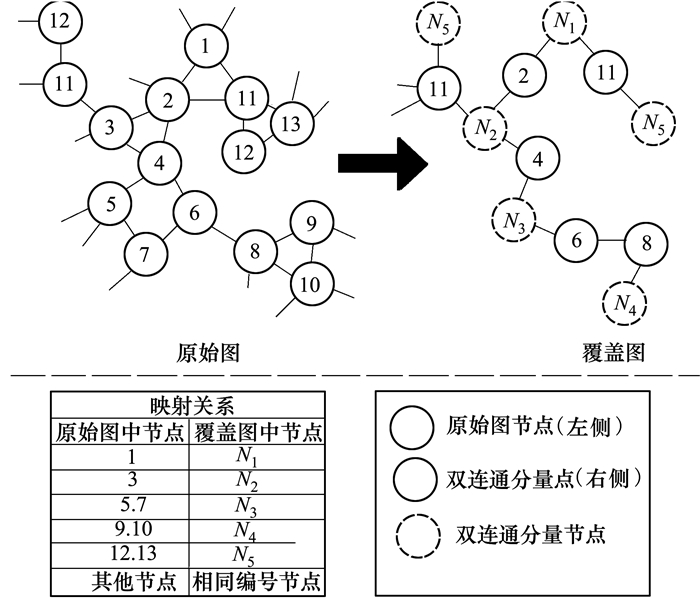
2 算法算法的基本思想如图 2所示:①首先, 识别原始图中的双连通分量并缩成点以构建覆盖图, 建立原始图到覆盖图中节点的单射关系。②对原始图中节点对s和t, 寻找覆盖图中的对应点S和T。③覆盖图中S和T之间路径上每个U类节点对应原图中的一个双连通分量, U类节点在路径上前后两个节点是双连通分量的界点, 则可并行求解每个双连通分量的2个界点之间的最大流。④合并子问题结果得到原始图中节点对s和t最大流的解。

|
| 图 2 最大流加速方法整体流程 |
|
| 图 3 双连通分量覆盖图构建示意图 |
左侧原始图可转换为右侧覆盖图, 覆盖图中的实线节点对应原图中相同编号的割点, 覆盖图中虚线节点对应左侧原图中的双连通分量; 其中, 原始图到覆盖图的映射关系在图中下方的表格中。对于原图中节点1和10的最大流, 由于对应的N1和N4之间的唯一路径包含界点2/4/6/8, 则原图中节点1和节点10最大流可分解为(1, 2), (2, 4)(4, 8)(8, 10)4个并行的最大流计算, 从而大幅降低求解时间。注意此时各个界点间的计算仅涉及对应的双连通分量内的节点, 即此时原图中节点1和10之间的所有最大流路径, 不可能包含覆盖图中路径上之外的节点, 例如此时N2的另外一个界点为11, 且根据定义必为割点, 则最大流路径不可能涉及节点12所在的双连通分量除11之外的节点, 否则节点11必然在路径中出现2次, 违反了最大流路径为简单路径的定义。这也意味着, 基于覆盖图可排除部分节点, 这也可降低计算量。
根据引理2, 我们给出了递归的覆盖图构建算法, 如表 1所示。
| input:当前节点nodei, 节点深度depthi, 邻居节点信息 |
| output:设置节点low值lowi, 更新的双连通分量覆盖树T′ |
| step1:初始化当前节点low值lowi=INF, 状态值statei=visiting, 初始化双连通分量覆盖树T′, 初始化全局堆栈stacko |
| step2:For nodei的每个邻居节点nodek |
| step2.1:if nodek是nodei在遍历过程中的父节点, continue |
| step2.2:if statek=unvisited |
| step2.2.1 :设置nodek的深度depthk=depthi+1 |
| step2.2.2:将边(nodei, nodek)压到堆栈stacko中 |
| step2.2.3:以nodek为参数调用当前过程proc_shink |
| step2.2.4:tempk=lowk |
| step2.3:elseif statek==traversing, 设置临时变量.tempk=depthk |
| step2.4:else设置临时变量tempk=lowk |
| step2.5:If lowi>tempk, lowi=tempk |
| step2.6:If statek==visited and lowk>=depthi |
| step2.6.1:if nodei的割点标识is Cuti==false |
| step2.6.1.1 :设置当前节点nodei的割点标识is Cuti=true |
| step2.6.1.2:在T′中添加原图割点对应的W类节点, 记录在T′中的id为nodeW |
| step2.6.2:在T′中添加原图双连通分量对应的U类节点, 记录在T′中的id为nodeU |
| step2.6.3:从stacko中循环弹出边, 直到遇到边(nodei, nodek) |
| step2.6.4:标记包括(nodei, nodek)在内的所有已弹出边中非割点对应节点nodeU |
| step2.6.5:在T′中节点nodeU和nodeW间建立一条边 |
整个构建过程首先确定一个根节点, 按照深度优先的顺序在每个节点上递归调用固定的算法, 在单个节点上调用的递归算法。算法识别各个双连通分量, 同时更新对应的双连通分量覆盖树T′, 并建立双连通分量覆盖树中节点到原图节点的映射关系。算法1在运行时, 表 1中递归调用结束时step1会被调用N次, step2会被调用2M次, 而step2中包含循环的步骤为step2.6.3和step2.6.4, 由于对每条边只会调用1次, 全局共被调用M次, 则算法1的复杂度为O(N+M), 在稀疏大图中远小于最大流算法复杂度下限O(NM)[1]。这说明构建算法复杂度较低, 和图的规模呈线性关系。
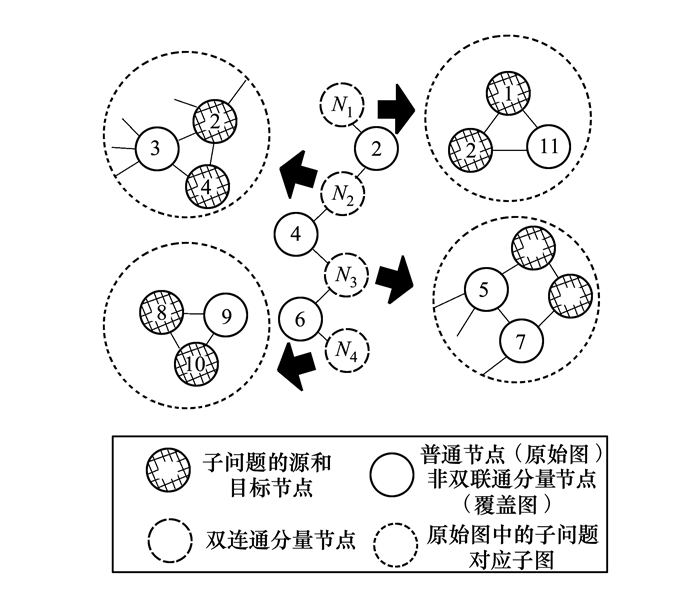
2.2 基于覆盖图的最大流加速方法基于覆盖图的加速方法包含图 2流程图的所有步骤, 其示例如图 4所示。
|
| 图 4 基于双连通分量覆盖图的最大流加速示意图 |
针对图 3中原始图中节点1到节点10的最大流问题, 基于映射表查询得到图 4的覆盖图中节点N1和N4。在双连通分量缩点树T′中搜索并发现如图 4中N1至N4的唯一路径; 路径上每个双连通分量节点对应一个子问题(如图 4中左右两侧的虚线圆圈), 通过并行求解子问题可进一步提高计算速度。
对应的最大流加速算法2如表 2所示。
| input:给定原始图中的节点s, t |
| output:最大流值和对应的多路径 |
| step1:If原始图未构建双连通分量覆盖图 |
| step1.1选择原始图中某个节点为根节点 |
| step1.2在根节点调用算法1, 递归构建双连通分量覆盖树 |
| step2:查询s和t在双连通分量覆盖树中的对应节点Vs和Vt |
| step3:If Vs和Vt不是双连通分量覆盖数中同一个节点 |
| step3.1搜索Vs和Vt之间的唯一路径(Vs, …W1, W2, …, WL, …Vt), 其中W1, W2, …, WL是路径上的W类节点 |
| step3.2分别在对应的双连通分量内并行计算(s, n1w), (n1w, n2w), …, (nLw, t)多个节点对之间的最大流, 其中路径上W类节点Wk(1≤k≤L)对应的原图割点为nkw, 直到所有节点对计算结束 |
| step3.3取所有最大流值的最小值作为全局最大流值, 每个最大流路径连接起来作为结果路径, |
| step3.4对每个节点对之间最大流路径上所有边的流量值, 按对应最大流和全局最大流最小值的比值等比降低. |
| step4:elseif Vs和Vt是双连通分量覆盖数中同一个节点 |
| step4.1直接在对应的双连通分量中计算(s, t)之间的最大流 |
首先会根据需要构建覆盖图, 之后在双连通分量覆盖树T′中找到源和目标对应的节点, 获取T′中的唯一路径, 将路径拆分为若干子路径, 同时计算并汇总得到最终结果, 其中step1为覆盖图构建过程, 可单独调用或在第一次计算时调用, 对给定图只调用一次; step2~4是针对单个源和目标节点对的计算步骤。算法2中step1即调用算法1, 其复杂度如上分析为O(N+M); 通过在算法1中建立Hash表存储映射关系, step2复杂度可低至O(1), 相对其他步骤可忽略不计; step3.1是一个树中的搜索过程, 在最坏情况下(树是一个线性序列)复杂度也仅为O(N); step3.2的复杂度取决于所有子问题中复杂度最高的那个子问题, 设为O(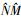
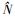
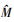
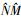
我们在基准评测图中分析和比较算法的加速效果, 每个图的参数主要包括节点数量N和无向边的数量M。对每个(N, M)组合, 采用权威评测工具GENRMF生成50个基准图, 每个图选取50个节点对分别计算最大流。GENRMF工具接收a, b, c1和c2(>c1)4个参数, 首先会产生b个拥有a个节点的子图, 随机分配顺序号给每个子图中节点, 并将其与前后2个相邻编号的节点相连; 每个子图也随机获得一个顺序号, 与前后2个相邻编号的子图做节点一对一的映射并建立连接。每个图中, 边的容量在c1和c2之间随机分布, 节点数量N=ab, 无向边数量M=a(2b-1), 在此基础上随机增加边以得到对应的边数量M。因M≥6N后并行度变化不大, 实验主要考察M≤5N的稀疏图中的变化情况。
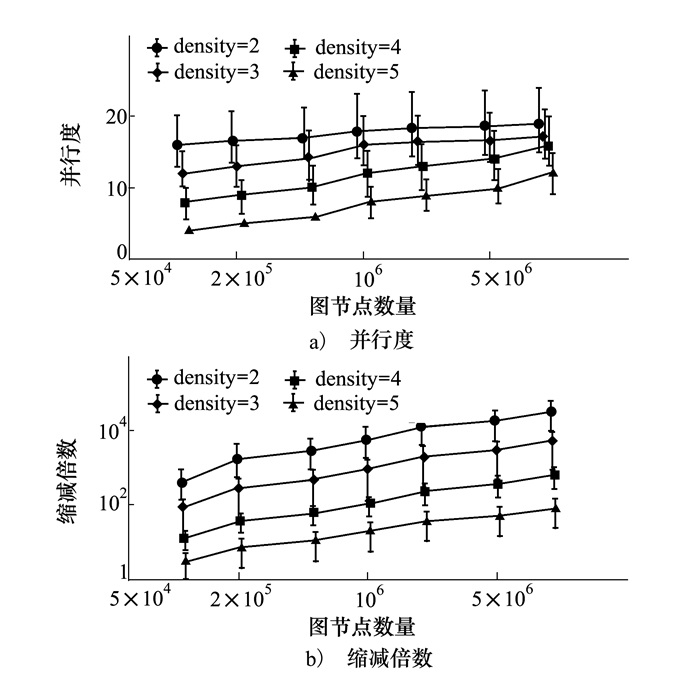
首先考察多个图中多次计算时并行度的均值及最大和最小值变化趋势, 如图 5a)所示, 其中稀疏度(density)定义为M/N。图 5a)表明并行度(及最大/最小值)均随节点数量N的增加或稀疏度的降低有缓慢增加, 不同稀疏度下的并行度均值随着N的增加逐渐趋向接近, 说明算法在稀疏大图中始终能保持合适的并行度。随着节点数量的增大, 并行度的区间有增大趋势, 稀疏度较高时区间范围随节点数量增大增加趋势更快, 例如在N=107时所有稀疏度下的最小值也能达到接近10左右, 保证最差情况下的加速效果。
|
| 图 5 基准图中并行度和缩减倍数的变化趋势 |
我们也考察缩减倍数均值及最大最小值的变化趋势, 如图 5b)所示, 其中Y轴为指数坐标系。可发现, 缩减倍数均值和节点数量大致呈指数关系, 且均值(及最大/最小值)随节点数量N的增加或稀疏度的降低有缓慢的增加。随着节点数量的增加, 各种稀疏度下的缩减倍数均有指数级的增加, 并不随着稀疏度变化有明显降低。且随着节点数量的增大, 区间也有明显的变大趋势(注:Y轴为指数坐标系)。另外缩减倍数最小值始终都有增大的趋势, 但是在稀疏度较高和节点数量较低时可能会很小, 如N=105且稀疏度为5时为1左右, 此时整个原图即为一个双连通分量, 从而使得最大流计算需涉及原图中所有节点。
基于前述理论分析, 我们在上述基准网络上比较我们的算法和经典算法的效果。硬件环境为ThinkStation P310工作站, 拥有2颗4核CPU和32GB内存, CPU主频2.6GHz, 操作系统采用CentOS7.0.并行计算时开启8个线程, 每线程对应一个CPU核; 计算时将所有子问题组织成先进先出队列, 依次将问题调度给空闲的线程。已知面向通用最大流求解的串行算法是基于highest push/relable的方法[22], 因此在各类图缩减算法计算时均默认采用highest push/relable计算缩减图中的最大流, 比对的各类算法标记如下:
Clique:文献[10]基于局部子图缩减的最大流求解方法, 检测子图特征时使用了最大团方法。
Community方法:文献[10]中基于网络社区结构缩减的最大流求解方法。
VertexPair:文献[15]中基于节点对的缩减方法。
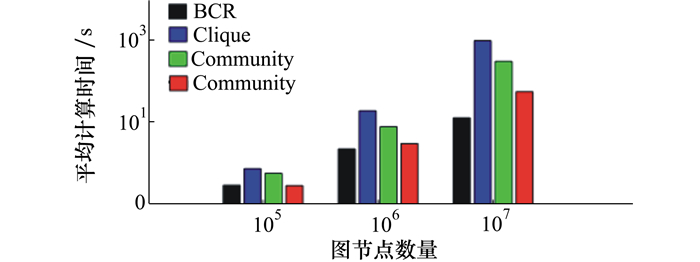
实验中针对3个不同的节点数量N, 从基准图中随机选择各种稠密度的50幅图, 每幅基准图中选取50个不同节点对分别进行最大流计算, 并记录各种不同方法中除去数据载入和输出的计算时间, 如图 6所示, 其中X轴分别对应节点数量N=105, 106, 107, Y轴为按对数坐标显示的计算时间。此时我们算法BCR对应X轴3个坐标点的计算时间均值分别为0.3 s, 2.3 s, 13.2 s。可见仅N=105时VertexPair方法平均要稍快一些(约为我们方法的0.9倍左右时间), 其他方法以及在更大的图中, 我们方法都是最快的, 而且随着图规模的增加, 其他方法的计算时间呈指数级上升。检查数据发现, 由于Clique和Community方法寻找最大团和社团等无尺寸限制的子图结构, 而实际上由于算法限制, 稀疏图中能找到的子图结构并不多, 从而影响了加速效果; 随着图规模的增加, 相应的子图结构并没有同步变大, 使得缩减效果进一步降低, 导致加速效果变差, 而VertexPair基于局部的2个子节点进行缩减, 无论在何种图中都能充分找到可利用的子图结构, 从而保证一定的加速效果。
|
| 图 6 基准图中所有算法平均最大流计算时间对比 |
我们也比较了所有方法的预处理时间, 如图 7所示。我们算法中对应X轴3个坐标点的预处理时间均值分别为0.9 s, 8.7 s, 61.3 s。我们算法始终保持较低的预处理时间; 且随着图规模的增大, 在N=107时相对其他方法的优势更加明显; 检查对应的预处理算法发现, Clique和Community方法寻找无尺寸限制子图方法, 在原图增大时计算复杂度呈指数级增加; 而VertexPair方法优化后可维持线性的复杂度, 但整体上我们的预处理时间仍然最低。前述实验可得到如下结论:

|
| 图 7 基准图中所有算法平均预处理时间对比 |
1) 相对其他方法, 我们算法加速效果部分来自于排除作用, 即排除计算不会涉及的节点, 将计算相关节点缩减到一个很小的范围, 在大图中甚至可缩减到原图节点的万分之一左右, 大大加速计算速度; 加速效果的另外一个来源是并行计算的引入, 通过将原始的最大流问题分隔成多个独立的可并行求解的子问题, 可充分利用底层设施的并行性加速计算; 且由于独立子问题数量不会太多, 对基础设施要求也较低。
2) 相比基于大范围子图方法Clique和Community, 我们的算法加速效果更明显, 且前期处理时间也大幅领先; 我们的算法对于VertexPair这种针对局部小型子图的方法也有优势。上述优势随着图尺寸的增加而增加, 也说明了我们方法更加适用于大规模稀疏图。
4 结论本文提出基于双连通分量覆盖图的稀疏大图最大流并行加速方法, 算法采用双连通分量建立覆盖图, 将原始图中最大流问题分解为多个子图中的局部问题, 基于并行计算加速求解。在大量基准图上的分析和实验表明, 算法具极低的覆盖图构建代价, 相比已知算法可达到2个数量级的加速效果。将来的工作可从多个角度展开, 包括寻找稠密大图中的最大流并行加速方法, 及如何在分布式计算框架上实现基于覆盖图的加速计算。
| [1] | Goldberg A, Tarjan E. Efficient Maximum Flow Algorithms[J]. Communications of the ACM, 2014, 57(8): 82-89. DOI:10.1145/2632661 |
| [2] | Liang C, Yu F R, Zhang X. Information-Centric Network Function Virtualization over 5g Mobile Wireless Networks[J]. IEEE Network, 2015, 29(3): 68-74. DOI:10.1109/MNET.2015.7113228 |
| [3] | Kosut O. Max-Flow Min-Cut for Power System Security Index Computation[C]//IEEE Sensor Array and Multichannel Signal Processing Workshop, 2015: 61-64 |
| [4] |
陈晓旭, 吴恒, 吴悦文. 基于最小费用最大流的大规模资源调度方法[J]. 软件学报, 2017, 28(3): 598-610.
Chen Xiaoxu, Wu Heng, Wu Yuewen. Large-Scale Resource Scheduling Based on Minimum Cost Maximum Flow[J]. Journal of Software, 2017, 28(3): 598-610. (in Chinese) |
| [5] | Ford L R, Fulkerson D R. Notes on Linear Programming, Part Ⅱ: Maximal Flow through a Network[M]. Santa Monica, RAND Corporation, 1977: 16-31 |
| [6] | Karzanov A V. Determining the Maximal Flow in a Network by the Method of Preflows[J]. Doklady Mathematics, 1974, 15(1): 434-437. |
| [7] | Schiopu C, Ciurea E. The Maximum Flows in Planar Dynamic Networks[J]. International Journal of Computers Communications & Control, 2016, 11(2): 282-291. |
| [8] | Goldberg AV, Hed S, Kaplan H, Tarjan RE, Werneck RF. Maximum Flows by Incremental Breadth-First Search[C]//European Symposium on Algorithms, 2011: 457-468 |
| [9] | Ghaffari M, Karrenbauer A, Kuhn F. Near-Optimal Distributed Maximum Flow: Extended Abstract[C]//ACM Symposium on Principles of Distributed Computing, 2015: 81-90 |
| [10] | Sherman J. Nearly Maximum Flows in Nearly Linear Time[C]//IEEE Symposium on Foundations of Computer Science, 2013: 263-269 |
| [11] | Liers F, Pardella G. Simplifying Maximum Flow Computations:The Effect of Shrinking and Good Initial Flows[J]. Discrete Applied Mathematics, 2011, 159(17): 2187-2203. DOI:10.1016/j.dam.2011.06.030 |
| [12] | Dan G. Very Simple Methods for All Pairs Network Flow Analysis[J]. Siam Journal on Computing, 1990, 19(1): 143-155. DOI:10.1137/0219009 |
| [13] | Zhang Y, Xu X, Hua B. Contracting Community for Computing Maximum Flow[C]//IEEE International Conference on Granular Computing, 2012: 651-656 |
| [14] | Zhang Y P, Hua B, Jiang J, et al. Research on the Maximum Flow in Large-Scale Network[C]//International Conference on Computational Intelligence and Security(CIS), 2011: 482-486 |
| [15] | Scheuermann B, Rosenhahn B. Slimcuts: Graphcuts for High Resolution Images Using Graph Reduction[C]//International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition, 2011: 219-232 |
| [16] | Zhen C, Zhang L. The Computation of Maximum Flow in Network Analysis Based on Quotient Space Theory[J]. Chinese Journal of Computers, 2015, 38(8): 1705-1712. |
| [17] | Niklas B, Blelloch G, Shun J. Efficient Implementation of a Synchronous Parallel Push-Relabel Algorithm[C]//European Symposia on Algorithms, 2015: 106-117 |
| [18] | Soner S, Ozturan C. Experiences with Parallel Multi-Threaded Network Maximum Flow Algorithm[J]. Partnership for Advanced Computing in Europe, 2013, 2013(1): 1-10. |
| [19] | Benoit D, Dupont E, Zhang W. Distributed Max-Flow in Spark[EB/OL]. (2015-06-03)[2017-04-06]. http://stanford.edu/~rezab/classes/cme323/S15/projects/distributed_max_flow_report.pdf |
| [20] | Halim F, Yap R, Wu Y. A Mapreduce-Based Maximum-Flow Algorithm for Large Small-World Network Graphs[C]//International Conference on Distributed Computing Systems(ICDCS), 2011: 192-202 |
| [21] | Goldfarb D, Grigoriadis M D. A Computational Comparison of the Dinic and Network Simplex Methods for Maximum Flow[J]. Annals of Operations Research, 1988, 13(1): 81-123. DOI:10.1007/BF02288321 |
| [22] | Goldberg, A V. Two-Level Push-Relabel Algorithm for the Maximum Flow Problem[C]//The Fifth Conference on Algorithmic Aspects in Information Management, 2009: 212-225 |


