2. 中国科学院 遥感科学国家重点实验室, 北京 100101
点集匹配在图像分析、形状匹配等许多领域中已获得广泛的应用[1-2],可粗略的分为刚性和非刚性,其中非刚性匹配问题备受关注。但由于点集中通常包含大量异常值,这严重影响了匹配性能,因此需要研究更稳健的点集匹配算法。
近些年,基于混合高斯模型(Gaussian mixture model, GMM)的匹配方法更是受到了研究者的广泛关注[3]。在最大似然估计框架下,利用最大化期望(expectation maximization, EM)算法求解参数的最大似然估计。Jian等[4]用混合高斯模型表示点集,通过最小化2个混合高斯之间的统计差异,进而确定点集之间的对应关系。Myronenko等[5]假设点集做一致性运动,提出了基于一致性点漂移(coherent point drift, CPD)的点集匹配方法,通过增加额外的均匀分布模型化异常值。但它本质上对应于最小二乘方法,对异常值不稳健。为了提高对异常值的稳健性,一种可选的方法是选用更合适的概率模型,如具有厚尾性质的t分布[3]。Zhou等[6]提出用混合t分布模型(student′s t mixture model, SMM)处理点集之间的匹配问题,通过最大化似然函数的对数期望,估计变换参数。但是它和CPD方法以及多数方法一样,只允许各向同性协方差,而且需要手动确定正则化参数。
针对最大似然估计框架中存在的奇异性问题,可选的解决方式是贝叶斯分析[7-8]。Qu等[9]提出了在变分贝叶斯框架下的点集匹配方法(VBPSM),将点集匹配过程分为聚类分析和回归分析两部分,并分别利用2个GMM模型化,通过引入转移变量将两部分统一起来。但对于非刚性变换,它没有包含对变换函数的平滑性约束。另一个问题是估计的变换函数没有直接反映待对准点集之间的变换关系。在Simpson等[10]提出的非刚性配准的概率配准框架中,通过给变换参数指派一个合适的先验分布可将正则化并入概率框架中,根据数据质量自适应地确定正则化参数。
贝叶斯SMM已经广泛应用到了密度估计、聚类和模型选择中[11-12]。Archambeau等[12]在估计变量的后验分布过程中,考虑了变量之间的相关。Baldacchino等[13]将贝叶斯SMM应用于非线性系统识别中的稳健回归。
综上,针对存在异常值的非刚性点集匹配问题,本文将点集匹配问题表示为SMM对应的概率密度估计问题。通过引入真实后验分布的变分近似,匹配问题转化为最大化变分下界,同时允许任何形式的协方差。在参数推断过程中,利用变分贝叶斯最大化期望(variational Bayesian EM, VBEM)算法确定变换参数。通过先验模型,将空间正则化约束并入贝叶斯SMM模型中,可自适应地确定正则化参数。模拟点集和真实图像上的实验结果证明所提方法可大大提高匹配性能。
1 贝叶斯混合t分布模型设数据点集和模型点集分别记为X={xn}n=1N和Y={ym}m=1M, 其中xn, ym∈RD表示点的空间位置, D为空间维数, N和M分别为特征点个数, 齐次坐标记为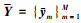
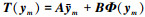
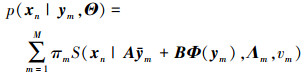
|
(1) |
式中, Θ={A, B, {Λm}, {πm}, {vm}}, t分布的概率密度函数为:
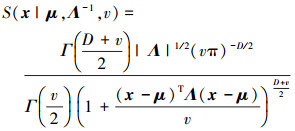
|
(2) |
式中,μ和Λ分别为均值向量和精度矩阵, Γ(·)为伽玛函数, 当自由度参数v→∞时, t分布收敛到高斯分布。t分布可表示为无限个具有相同均值、不同精度的尺度高斯分布的混合, 即:

|
(3) |
式中,N(x| μ, Λ-1)和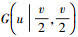
为了便于变分, 引入离散二值示性变量Z={zn}n=1N和尺度变量U={un}n=1N, 记为隐变量ΘL={ U, Z }, 其中znm∈{0, 1}, 且
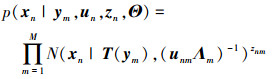
|
(4) |
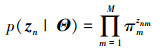
|
(5) |

|
(6) |
于是, 似然函数可写为:
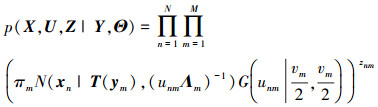
|
(7) |
利用指数族分布的共轭先验特性, 选择模型变量的先验:①混合比例系数π的先验分布服从狄利克雷分布Dir(π|κ0), 其中κ0是先验样本大小(称为超参数, 下同); ②每个混合成分的精度矩阵Λm的先验分布服从Wishart分布W(Λm|γ0, S0), 其中γ0和S0分别为自由度和尺度矩阵; ③仿射变换矩阵A和非刚性形变系数矩阵B的每列元素的先验分布分别服从零均值向量、精度参数υ和η的高斯分布; ④精度参数向量υ和η均服从伽玛分布, 其中a0, b0和c0, d0分别是先验形状和尺度参数对; ⑤正则项以先验形式并入贝叶斯SMM模型中[10], 即:
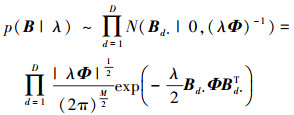
|
(8) |
式中,λ>0是标量正则化参数; ⑥正则化参数λ服从形状参数为τ0和尺度参数为ζ0的伽玛分布。可根据经验确定超参数的值。通过变分推断, 可获得变量{ΘL, ΘVB}={ΘL, { A, B, Λ, π, υ, η, λ }}的后验分布, 由于没有自由度参数v={vm}的先验, 利用最大似然方法可确定它的值, 记为ΘML={v}, 详见下一节。
变量之间的联合分布可表示为:

|
(9) |
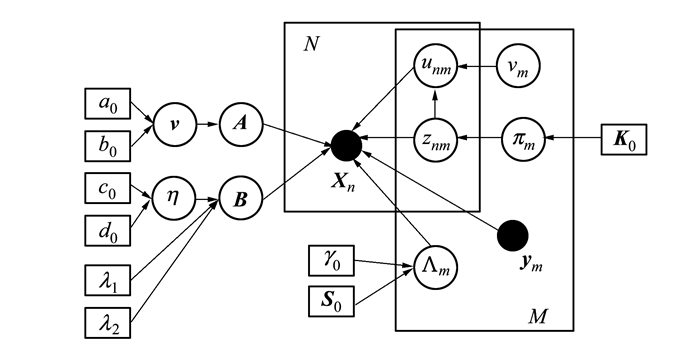
图 1中给出了非刚性点集匹配对应的概率图模型, 即有向无环图[7]。
|
| 图 1 非刚性点集匹配的概率图模型 |
考虑近似后验分布q(U, Z, ΘVB), 对数似然函数可表示为:
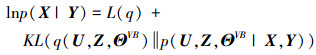
|
(10) |
式中,KL(q(U, Z, ΘVB) p(U, Z, ΘVB|X, Y)) ≥0度量真实后验分布p(U, Z, ΘVB|X, Y)和近似后验分布q(U, Z, ΘVB)之间的Kullback Leibler(KL)散度, 当且仅当q(U, Z, ΘVB)=p(U, Z, ΘVB|X, Y)时等式成立。故L(q)是lnp(X|Y)的近似下界, 通过变分推断可获得{ΘL, ΘVB}的近似后验分布。
所有变量的后验分布可分解为:
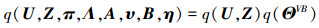
|
(11) |
记q(ΘVB)=q(π)q(Λ)q(A)q(υ)q(B)q(η)q(λ)。关于q(U, Z)和q(ΘVB)分别最大化L(q)可获得如下VBEM算法, 在第k次迭代:
VBE-step:
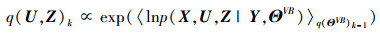
|
(12) |
VBM-step:
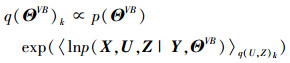
|
(13) |
式中,〈·〉q(·)表示关于后验分布q(·)的期望, 后面下标省略。在变分贝叶斯期望步骤(VBE-step)中, 固定变分变量ΘVB, 计算隐变量ΘL的后验分布; 在变分贝叶斯最大化步骤(VBM-step)中, 固定隐变量ΘL, 重新计算ΘVB的后验分布。下面列出部分变量的后验分布:
1) 考虑隐变量之间的相关性, 其后验分布为:

|
(14) |
式中,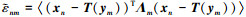
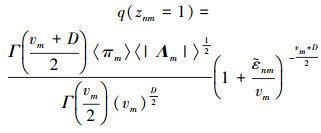
|
(15) |
规范化后, 示性变量元素表示为:
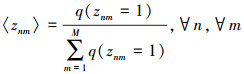
|
(16) |
以示性变量为条件, 尺度变量的后验分布服从伽玛分布:q(unm|znm=1)~G(unm|αnm, βnm), 其中
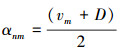
|
(17) |
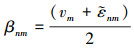
|
(18) |
根据伽玛分布性质, 有
2) 仿射变换矩阵A的第q行元素的后验分布仍服从高斯分布: 
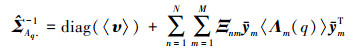
|
(19) |
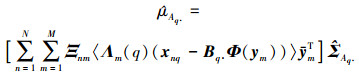
|
(20) |
式中,diag(〈υ 〉)表示〈υ 〉中元素构成的方阵, 矩阵Ξ的元素为Ξnm:=〈znmunm〉, Λm(q)表示Λm的第q个对角元素。
3) 非刚性形变系数矩阵B的第q行元素的后验分布服从高斯分布: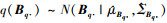
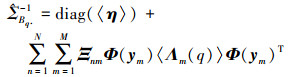
|
(21) |

|
(22) |
4) 正则化参数λ的后验分布服从伽玛分布:q(λ)~G(λ|τ, ζ), 其中

|
(23) |
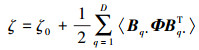
|
(24) |
根据伽玛分布性质, 有〈λ〉=τ/ζ, 可根据不同的应用自适应地确定λ的值。
其余变量的后验分布见附录。由于没有自由度参数{vm}的先验, 可直接最大化下界L(q), 获得下面非线性方程:
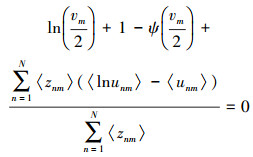
|
(25) |
利用斯特林公式[14] 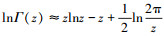


|
(26) |
这可避免非线性方程的求解。由于L(q)的计算可能涉及大矩阵的计算, 故在本文的算法中, 通过计算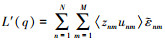
算法1:基于SMM的非刚性点集匹配算法
1:输入: X={xn}n=1M, Y={ym}m=1M, 容忍误差εF
2:初始化:
先验: a0, b0, c0, d0, κ0, γ0, S0, τ0, ζ0
变换: A, B
3: for S0上由粗到精do
4: repeat
VBE-step:
根据(15~16)推断示性变量Z
根据(17~18)推断尺度变量U
VBM-step:
根据(27)更新混合比例系数π的κ
根据(19~20)推断仿射变换矩阵A
根据(30~31)推断精度υ的a和b
根据(21~22)推断非刚性形变系数矩阵B
根据(32~33)推断精度η的c和d
根据(28~29)更新精度Λ的γ和S
根据(23~24)更新正则化参数λ的τ和ζ
根据(26)更新自由度v
计算第k步的L′(q)
5: until|L′k-L′k-1| < εF
6: end for
算法的时间复杂度主要由Z, Λ和B的后验更新决定。在每次迭代中, 更新这些变量的时间复杂度分别近似为O(DNM2), O(D2(N+D)M)和O(DM3), 一般情况下, D≪N, M, 故算法的总时间复杂度可近似为O(KM3)或O(KNM2), 其中K为迭代次数。
3 实验结果与分析为了验证本文算法的有效性, 首先测试具有形状差异的模拟数据集, 然后将本文方法应用于包含非刚性形变的图像。并与5种算法进行了对比:GMM-L2[4], CPD[5], SMM[6]和VBPSM (默认各向异性协方差)[8]和TPS-RPM[15]。超参数的值设置如下:①超参数a0, b0, c0, d0, τ0和ζ0设定为0.01;②κ0的元素设定为M; ③γ0设定为2×(D+1), 若选择各向异性协方差, 则S0设定为单位矩阵I, 否则设定为标量1;④高斯径向基函数的宽度参数设定为1。针对各向异性和各向同性协方差2种选择, 本文方法分别记为VBSMM(ANI)和VBSMM(ISO)。
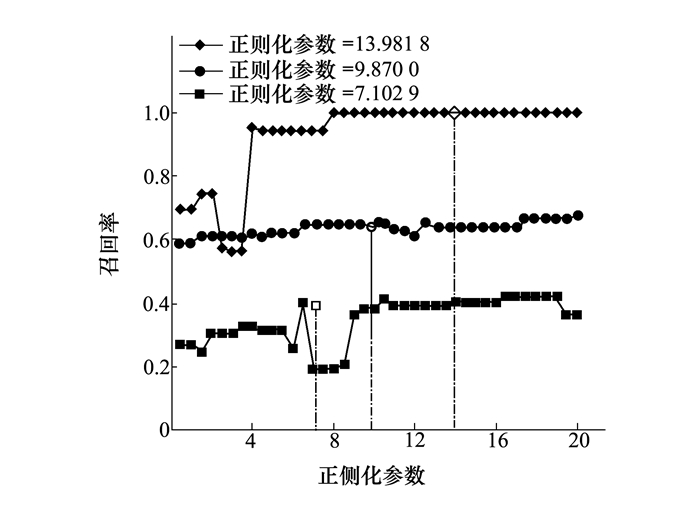
3.1 自适应确定正则化参数的有效性为了检验自适应确定正则化参数的有效性, 选用文献[15]中公共数据集的3组存在异常值的汉字福形状点集, 记录算法1在固定正则化参数时获得的匹配召回率(recall), 其中正则化参数的固定取值为0.5k, k=1, 2, …, 40, 并与算法1在自适应确定正则化参数时获得的匹配召回率做对比。图 2给出了召回率关于正则化参数的变化曲线, 其中空心对应于算法1在固定正则化参数时的匹配召回率, 实心对应于算法1在自适应确定正则化参数时的匹配召回率, 其中自适应确定的正则化参数分别为13.989 8, 9.870 0和7.102 9。从图中曲线可以看出, 算法1通过自适应方法总是能“自动”找到相对合适的正则化参数。这在批量处理点集匹配问题时, 可避免手动确定不合适的正则化参数。
|
| 图 2 召回率关于正则化参数的变化曲线(其中实心位置对应于算法1自适应确定的正则化参数) |
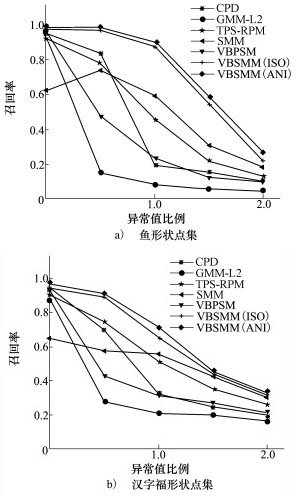
为评价对异常值的稳健性, 选用文献[15]中的公共数据集, 包含鱼和汉字福两种形状点集, 分别包含96和108个模型点。数据点样本包含5个异常值比例水平(从0.0到2.0), 对于每一个比例, 均有100个数据点集样本, 采用平均的召回率评价匹配结果。图 3给出了6种算法应用于2种形状点集的平均召回率统计结果。
|
| 图 3 6种算法应用于鱼和汉字福2种形状点集的召回率对比结果 |
从图中可看到, 随着异常值比例的增加, 所有的算法的匹配效果均迅速衰减, 其中GMM-L2方法最严重, 这主要是由于异常值破坏了点集的形状结构。但相比其他5种算法, 本文提出的VBSMM算法总是能给出较好的匹配结果。图 4给出了算法1在2种形状点集上的匹配结果示例。

|
| 图 4 本文算法在不同异常值比例下的匹配结果示例 |
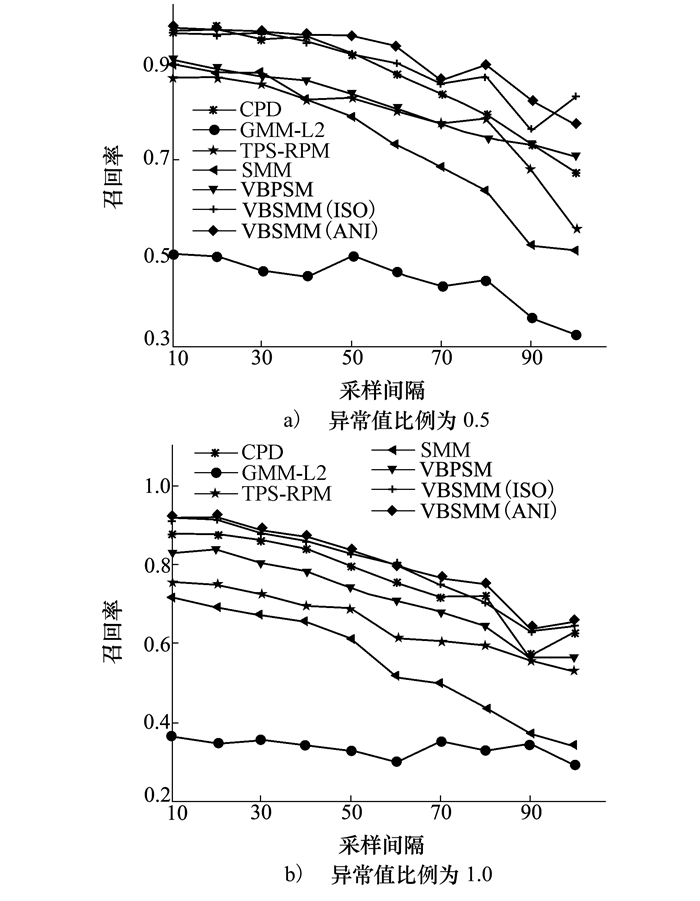
为验证本文算法对模型点集和数据点集中均存在异常值时的稳健性, 选用CMU房子序列(http://vasc.ri.cmu.edu/idb/html/motion/index.html), 其包含不同视角的111幅房子图像, 每个图像中标记出了30个已知对应关系的特征点。通过给每个点集增加不同数量服从均匀分布的异常值以生成待匹配点集, 其中异常值比例分别为0.5和1.0。基于采样区间10:10:100对图像序列进行采样, 可获得10组图像对。因为30个特征点的对应关系已知, 故可直接统计每个采样区间内的平均召回率。图 5比较了6种算法的平均召回率统计结果对比。从图中可以看出, 不同方法的性能出现了不同程度的震荡, 这主要是由于异常值生成的随机性。整体来看, 相比于其他5种算法, 本文提出的VBSMM算法更稳健, 这与3.2部分的实验结果一致。图 6给出了本文算法在不同异常值比例下的匹配结果示例(正确匹配对数均为30/30)。
|
| 图 5 6种算法应用于房子序列图像的召回率对比结果 |

|
| 图 6 本文算法在不同异常值比例下得匹配结果示例 |
本文针对存在异常值的非刚性点集匹配问题提出了贝叶斯SMM模型方法。在变分贝叶斯框架中, 该方法将点集匹配问题模型化为SMM对应的概率密度估计问题, 利用VBEM算法迭代更新变量的后验分布, 而且允许各向异性和各向同性协方差2种选择。通过先验模型引入正则化项, 可自适应地确定正则化参数。最后, 模拟点集和真实图像上的实验结果验证了本文所提方法的有效性。
附录:近似变分后验其他变量的后验分布如下:
1) 对于混合比例系数π, 其后验分布仍服从狄利克雷分布:q(π)~Dir(π| κ), 其中:
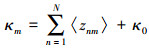
|
(27) |
2) 对于每个混合成分的精度矩阵Λm, 其后验分布仍服从Wishart分布:q(Λm)~W(Λm|γm, Sm), 其中:
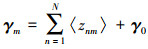
|
(28) |

|
(29) |
当选择各向同性协方差时, 混合成分的精度服从伽玛分布。
3) 对于精度参数υ, 其后验分布仍服从伽玛分布:q(υl)~G(υl|al, bl), 其中:
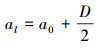
|
(30) |
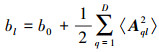
|
(31) |
4) 对于精度参数η, 其后验分布仍服从伽玛分布, q(ηl)~G(ηl|cl, dl), 其中:
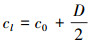
|
(32) |

|
(33) |
| [1] | Goshtasby A A. 2-D and 3-D Image Registration:for Medical, Remote Sensing, and Industrial Applications[M]. New Jersey: Voiley-Interscience, 2005. |
| [2] | Crum W R, Hartkens T, Hill D L G. Non-Rigid Image Registration:Theory and Practice[J]. The British Journal of Radiology, 2004, 77(Suppl 2): 140-153. |
| [3] | McLachlan G, Peel D. Finite Mixture Models[M]. New York: John Wiley & Sons, 2004. |
| [4] | Jian B, Vemuri B C. Robust Point Set Registration Using Gaussian Mixture Models[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1633-1645. DOI:10.1109/TPAMI.2010.223 |
| [5] | Myronenko A, Song X. Point Set Registration:Coherent Point Drift[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2010, 32(12): 2262-2275. DOI:10.1109/TPAMI.2010.46 |
| [6] | Zhou Z Y, Zheng J, Dai Y K, et al. Robust Non-Rigid Point Set Registration Using Student's-T Mixture Model[J]. PloS One, 2014, 9(3): e91381. DOI:10.1371/journal.pone.0091381 |
| [7] | Bishop C M. Pattern Recognition and Machine Learning[M]. New York: Springer-Verlay, 2006. |
| [8] | Blei D M, Kucukelbir A, McAuliffe J D. Variational Inference:a Review for Statisticians[J]. Journal of the American Statistical Association, 2017, 112(518): 859-877. DOI:10.1080/01621459.2017.1285773 |
| [9] | Qu H B, Wang J Q, Li B, et al. Probabilistic Model for Robust Affine and Non-Rigid Point Set Matching[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2017, 39(2): 371-384. DOI:10.1109/TPAMI.2016.2545659 |
| [10] | Simpson I J, Schnabel J A, Groves A R, et al. Probabilistic Inference of Regularisation in Non-Rigid Registration[J]. NeuroImage, 2012, 59(3): 2438-2451. DOI:10.1016/j.neuroimage.2011.09.002 |
| [11] | Svensén M, Bishop C M. Robust Bayesian Mixture Modelling[J]. Neurocomputing, 2005, 64: 235-252. DOI:10.1016/j.neucom.2004.11.018 |
| [12] | Archambeau C, Verleysen M. Robust Bayesian Clustering[J]. Neural Networks, 2007, 20(1): 129-138. DOI:10.1016/j.neunet.2006.06.009 |
| [13] | Baldacchino T, Worden K, Rowson J. Robust Nonlinear System Identification:Bayesian Mixture of Experts Using the T-Distribution[J]. Mechanical Systems and Signal Processing, 2017, 85: 977-992. DOI:10.1016/j.ymssp.2016.08.045 |
| [14] | Impens C. Stirling's Series Made Easy[J]. The American Mathematical Monthly, 2003, 110(8): 730-735. DOI:10.1080/00029890.2003.11920013 |
| [15] | Chui H, Rangarajan A. A New Point Matching Algorithm for Non-Rigid Registration[J]. Computer Vision and Image Understanding, 2003, 89(2): 114-141. |
2. The State Key Laboratory of Remote Sensing Science, Chinese Academy of Sciences, Beijing 100101, China


