p-S-N曲线是结构工程中进行疲劳可靠性分析与耐久性设计的基础依据[1-2],现行估计p-S-N曲线的主要方法有基于最小二乘法的线性回归方法和极大似然法[3]。大量疲劳试验结果表明,疲劳寿命的概率分布随不同应力水平作用而不同,因此最小二乘法估计的p-S-N曲线不是线性无偏估计,近年来有学者提出采用异方差加权最小二乘法线性回归技术来估计p-S-N曲线[4]。
然而上述方法大多需要成组疲劳试验数据,由于疲劳试验需要耗费较多的时间和财力,各应力水平下的疲劳试验件数常少于10件,甚至只取3~5件。有学者提出在小样本条件下预测p-S-N曲线的方法,但大多集中在不同可靠度下应力-寿命模型中参数的确定性估计方面[5]。
近年来,基于变量不确定性谱分解的近似随机函数方法备受关注,非嵌入多项式混沌(non-intrusive polynomial chaos, NIPC)展开方法[6]是其之一,因其可采用较少试验数据便能有效估计响应量的概率特性,被广泛应用于结构力学、计算流体力学和可靠性分析等学科中[7]。本文基于NIPC展开方法,提出一种p-S-N曲线的小子样预测方法,主要技术思路是将应力-寿命模型中的参数视为随机变量,在较少应力水平下完成小子样疲劳试验,并运用优化算法反演寿命模型参数数值,由此获得应力-寿命模型参数的完整小子样数据集。将疲劳寿命变换为标准正态随机变量,并运用所得到的小样本模型参数数据对各参数进行关于标准寿命变量的NIPC展开,由此计算模型各参数对应试验应力水平的大子样数据集,继而完成各参数的边缘概率分布检验及参数间相关系数计算。在此基础上,运用最小二乘拟合方法获得模型参数统计特征值关于应力水平的定量关系,由此得到应力-寿命模型的全概率描述,即本文的p-S-N曲线。为提高前述方法的预测精度,本文额外选定其他应力水平的疲劳试验寿命对其进行了贝叶斯修正。通过铝合金2024-T3小子样疲劳试验数据,检验了本文方法预测中等寿命区概率疲劳寿命特性的有效性。
1 多变量概率函数的NIPC展开基于小子样疲劳寿命试验数据进行应力-寿命模型的概率分布预测是一个统计学的难题。利用数值大样本扩充方法是其基本方法途径,Bootstrap方法是早期的扩充样本方法之一,但对于样本数小于10的情况,仍效果不佳,且其主要目的是对统计量进行区间估计。本文的技术途径是利用NIPC的概率函数展开法来扩充应力-寿命模型中各参数的样本数据,进而完成基于小样本试验数据的p-S-N曲线预测。
NIPC是对随机函数进行其多项式响应面展开的方法,即采用多项式形式来近似表达一未知随机函数,其优点在于通过较少样本数据可获得随机函数的概率特性。
设ξ={ξ1, …, ξn}为一组独立同分布随机变量, 基于NIPC展开, 任意随机函数ϕ均可表示为随机变量组中各变量ξk(k=1, …, n)的正交多项式组合

|
(1) |
式中, Bm为m阶多项式, 公式为:
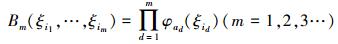
|
(2) |
式中,φad是单变量ad阶带权正交多项式, 且
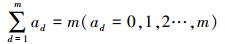
|
(3) |
假设截断式(1)右端项至p阶多项式, 即用有限项来近似ϕ, 将(1)式写成紧凑格式为
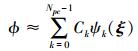
|
(4) |
于是, 随机函数ϕ分为两部分, 具有随机性质的多项式基函数ψk(ξ)和其确定性系数Ck。(4)式中的Npc为该展开式的项数, 可由下式来确定
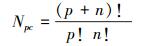
|
(5) |
式中, p为多项式展开最高阶数, n为随机变量个数。Npc亦为确定多项式确定性系数所需最小样本量。
(4) 式中正交多项式基函数的选择依赖于多项式中独立同分布随机变量的概率分布类型。根据Askey法则[6], 对应随机变量的不同概率分布, 存在不同的最优多项式基函数, 如当随机变量服从正态分布时, 对应的最优多项式基函数为Hermit多项式。当带权正交多项式的权函数与随机变量概率密度函数形式相同时, (4)式右端的有限项展开式随阶数p的增加依指数收敛于随机函数ϕ。
1.1 NIPC展开系数的确定NIPC展开方法最重要的环节是获得多项式混沌展开的各项系数Ck。一般情况下, 利用一定样本量(不少于由(5)式确定的数量, 最佳为2倍于Npc)的随机变量和随机函数值就可以计算出多项式混沌展开的系数。
对于n维输入随机向量ξ={ξ1, …, ξn}, 每取一组样本, 通过试验或数值模拟得到一个对应的输出ϕ*(ξ), 取Npc组样本, 由(4)式可得Npc个方程, 如(6)式所示, 由此即可解出各个系数值。

|
(6) |
当求出多项式各项系数之后, 即可计算随机函数ϕ的统计特性。由期望值定义
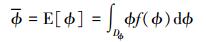
|
(7) |
式中, Dϕ是ϕ的积分域。由(4)式及多项式的正交性, 将(7)式中积分域Dϕ转换到随机变量ξ的积分域Dξ可得

|
(8) |
(8) 式说明随机函数ϕ的均值为多项式混沌展开式的0阶项。同理, 可以得到随机函数ϕ的方差

|
(9) |
式中,〈ψk2(ξ)〉为ψk2(ξ)在积分域中关于权函数的积分。
以上分析过程的计算流程如图 1所示。

|
| 图 1 NIPC展开法分析步骤 |
在金属材料疲劳分析中, 中等寿命区最常用的确定性模型为如下的Basquin幂函数式
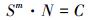
|
(10) |
式中, S为给定应力比下的应力幅值, N为疲劳寿命, m和C为模型参数。对(10)式两边取对数得
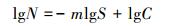
|
(11) |
在同一应力幅值下, 由于材料内在的不确定性, 疲劳寿命N总是随机的。以下分析中, 认为应力作用是确定量, 寿命N服从对数正态分布, 故(10)式中m和C也是服从某种分布的随机变量。
对于工程分析模型, 模型变量可分为以下3类:
1) 外部作用量, 如(10)式中的应力幅值S, 一般可认为是精确给定的;
2) 模型状态量, 如(10)式中的寿命N, 可由试验直接测得;
3) 模型内变量, 如(10)式中的m和C, 通常不可测, 但在前述参量已知条件下可通过模型反演的方法求解。
为使(10)式的确定性应力-寿命模型概率化, 本文提出以下方法与步骤予以完整实现。
2.1 m和C的概率化方法相应于每次试验寿命N的m和C值可通过(12)式优化反演获得
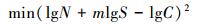
|
(12) |
在中等寿命区, m取值一般在(0, 10]之间, lgC取值一般在(0, 30]之间[1]。(12)式即为在约束条件下的最优解问题。
从统计抽样的观点, 对每一个试验寿命数据Ni, 由(12)式得到的mi和lgCi可认为是模型内变量的一次间接采样。由此得到的样本数据可分别用于建立各应力幅下m和lgC关于对数正则随机寿命N的NIPC展开式。
将每一试验应力水平下的小子样试验寿命进行对数正则化处理, 即转换为标准正态分布, 再运用(12)式计算得到的m(Si)和lgC(Si)数据进行NIPC展开, 即由小样本数据集(需满足(5)式的要求)按(6)式计算可得各展开式的系数。由这些NIPC展开式, 即可实施各应力幅下m(Si)和lgC(Si)的大容量样本快速计算, 随后按大子样EDF拟合优度检验其给定置信度下的边缘概率分布。取应力幅Si, 记由EDF检验得到的两模型内变量的边缘概率分布为:
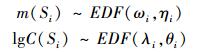
|
(13) |
式中, ωi, ηi, λi, θi为概率分布参数。
由(11)式知对数寿命为m和lgC的线性组合, 本文假设寿命服从对数正态分布, 由正态分布的可加性, 有理由假设m及lgC的联合概率分布服从二维正态分布N(μ1, σ12, μ2, σ22, ρ)。为此, 可对m和lgC的边缘概率分布((13)式)优先进行关于正态分布的EDF拟合优度检验, 同时可计算应力-寿命模型中两内变量间对应某应力幅下的相关系数如下:
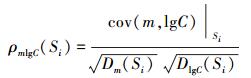
|
(14) |
为获得模型内变量概率分布参数及其相关系数关于应力幅的关系, 运用最小二乘拟合计算可得:
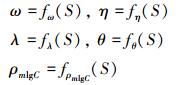
|
(15) |
由此计算步骤, 即可得到任意应力幅值下m和lgC的概率分布特性。
2.2 贝叶斯更新方法上述大样本数据计算过程中必然存在先验假设及模型误差问题。首先, NIPC展开过程中, 假设疲劳寿命N服从对数正态分布, 且对数正则化过程中只能使用小子样试验数据估计其均值和标准差; 其次, (15)式的拟合过程会存在拟合误差。为适当解决前述矛盾, 本文提出一种利用贝叶斯更新方法修正上述误差的方案:
1) 另取一组应力幅下的小样本疲劳试验数据, 按前述方法计算m和lgC的样本数据;
2) 将获得的样本数据代入贝叶斯公式, 对m和lgC的分布参数进行修正。在前述各应力水平下, m和lgC的概率分布类型可通过(13)式的EDF拟合优度检验确定, 且其在此应力水平下的概率分布参数可由(15)式计算得到, 作为贝叶斯更新的先验分布参数。
假设m和lgC通过关于正态分布的EDF检验, 可认为其服从二维正态分布N(μ, Σ), 贝叶斯修正后m和lgC的均值和协方差联合后验分布为(16)式所示的Normal-inverse-Wishart。
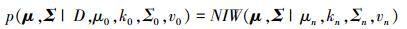
|
(16) |
式中, μ和Σ的后验分布参数为:

|
(17) |
式中, n为新增样本的容量, μ0, κ0, α0和β0分别为μ和Σ的先验分布参数;
3) 将步骤2得到的贝叶斯修正后模型参数视为原拟合(15)式的新增数据实例, 重新拟合m和lgC的概率分布参数关于应力幅的关系, 由此改进这些概率分布参数的拟合精度。
2.3 模型参数的抽样方法为预测任意应力幅值下疲劳寿命的概率特性, 需对m和lgC进行大子样抽样。由于m和lgC之间的相关性, 需将其等效地变换成独立正态分布才能进行抽样, 目前常用的变换方法为Nataf变换, 其是基于Copula函数变换的一种特例, 理论上适用于任意分布的变换, 但对于正态化程度较好的变量具有较高精度, 适用范围广, 其基本原理如下。
设有n维随机变量X=(X1, X2, …Xn)T, 已知各变量边缘概率密度函数为fi(xi), 累积分布函数为Fi(xi), 相关系数矩阵为ρ=(ρij)n×n。定义n维标准正态随机变量Y=(Y1, Y2, …, Yn)T, 其相关系数矩阵为ρ0=(ρ0ij)n×n, 相应的联合概率密度函数为
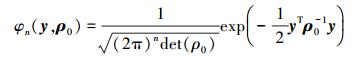
|
(18) |
根据等概率变换原则可得X和Y中的变量有如下关系
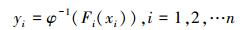
|
(19) |
根据Nataf变换理论, 利用隐函数求导法则, 由(19)式可推导出变量X的联合概率密度函数为
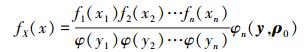
|
(20) |
根据相关系数定义及(19)式和(20)式可得随机变量X各变量间的相关系数与对应的标准正态变量Y各变量间的相关系数有以下关系
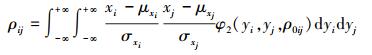
|
(21) |
当Xi和Xj的边缘分布及相关系数ρij已知时, 通过数值求解(21)式可得Yi和Yj的相关系数ρ0ij。
ρ0是一对称正定矩阵, 对其进行Cholesky分解可得下三角矩阵Γ0, 左乘Γ0的逆可将相关标准正态变量Y转化为独立标准正态变量U:
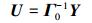
|
(22) |
至此, 采用拉丁超立方抽样方法对独立标准正态变量U抽样, 再对其进行上述变换的逆过程, 如(23)式所示, 即可得到随机变量X的样本。
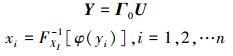
|
(23) |
为验证上述方法的有效性, 本文在中等寿命区完成了4组不同应力水平下带孔板的疲劳试验。由(11)式可知, 双对数坐标的寿命与应力幅满足线性关系, 故本文选取其中2组应力水平下的试验寿命样本, 确定m和lgC概率特性, 并拟合其统计特征值与应力水平的关系, 然后对第3组应力水平下的模型参数进行贝叶斯更新, 并拟合修正各参数统计特征值与应力水平关系的系数, 最终预测第4组应力水平下的概率疲劳寿命并与试验寿命进行对比。
疲劳试验件构型如图 2所示, 图中所标注尺寸单位为mm, 材料为铝合金2024-T3。

|
| 图 2 疲劳试验件构形 |
疲劳试验获得的寿命列于表 1, 应力比均为0.06。
| 组别 | S/MPa | 试验寿命/应力循环数 |
| A | 88.59 | 22 226, 23 435, 22 135, 23 410, 23 752, 22 651, 23 067, 24 808, 23 136, 23 451 |
| B | 52.78 | 164 457, 180 280, 199 233 |
| C | 33.47 | 931 175, 1 017 854, 1 065 166, 1 069 414, 1 188 311, 1 257 910, 772 159, 792 045, 1 561 126, 1 015 173 |
| D | 70.97 | 47 271, 52 777, 50 778, 47 325, 52 663, 53 352, 55 004, 52 272, 54 190, 56 097 |
试验机为MTS810.13±250 kN电液伺服万能试验机, 加载频率为20 Hz, 试验寿命为带孔板断裂时寿命。通过Bootstrap方法, 可获得A、C和D组应力水平下对数疲劳寿命均值μ和标准差σ的95%置信区间, 结果列于表 2, 为后文初步验证本文方法预测概率疲劳寿命参数的合理性做准备。
| 组别 | μ | σ |
| A | [4.271 1, 4.306 3] | [0.016 9, 0.045 0] |
| C | [5.868 3, 6.126 6] | [0.124 2, 0.329 6] |
| D | [4.692 0, 4.740 4] | [0.023 3, 0.061 7] |
由前述小节理论分析可知, 分别构建m和lgC关于疲劳寿命N的NIPC概率多项式函数, 由以下2个步骤完成:
1) 选定NIPC的基函数及阶数。由于疲劳寿命N服从对数正态分布, 可直接变换为服从标准正态分布的随机变量, 其对应的最优基函数为Hermit多项式。工程上一般取多项式阶数为3即可有效预测随机响应的概率特性。由(5)式可知此时仅需4个疲劳寿命N的样本。
2) 确定NIPC概率多项式函数的各项系数。将疲劳寿命N变换到标准正态空间作为多项式函数中随机变量的基本样本值, 即(6)式左端的输入矩阵, 由(12)式求出与各疲劳寿命N对应的m和lgC的值, 即(6)式右端的输出响应矩阵。求解(6)式即可获得构建的NIPC展开式各项系数。
由于不同应力水平下m和lgC的概率特性不同, 本文选取A、C 2组试验为例, 各自随机选取4个疲劳试验寿命, 采用NIPC方法获得各自的m和lgC关于lgN的Hermit多项式函数。在此基础上对疲劳寿命N进行抽样, 即可获得m和lgC的各自大样本, 此时仅是对多项式简单计算, 而并非求解(12)式的优化方程, 故节省大量计算时间。再通过m和lgC的大样本数据对其进行相关性检验和关于正态分布的EDF检验, 结果列于表 3, 表中Dn为上确界型统计量, W2和A2为平方差型统计量, 具体定义可参见相关文献[8]。
| 组别 | 变量 | μ | σ | 相关系数 | Dn | W2 | A2 |
| C | lgC | 12.151 6 | 0.043 3 | -0.882 7 | 0.680 2√ | 0.057 2√ | 0.376 1√ |
| m | 4.037 5 | 0.054 5 | 0.538 3√ | 0.054 6√ | 0.328 8√ | ||
| A | lgC | 12.050 6 | 0.006 5 | 0.421 9 | 0.824 2√ | 0.139 4√ | 0.812 5√ |
| m | 3.978 8 | 0.009 9 | 0.694 2√ | 0.102 5√ | 0.603 4√ | ||
| 注:表中, “√”表示在95%置信度下, 可接受各变量服从正态分布。 | |||||||
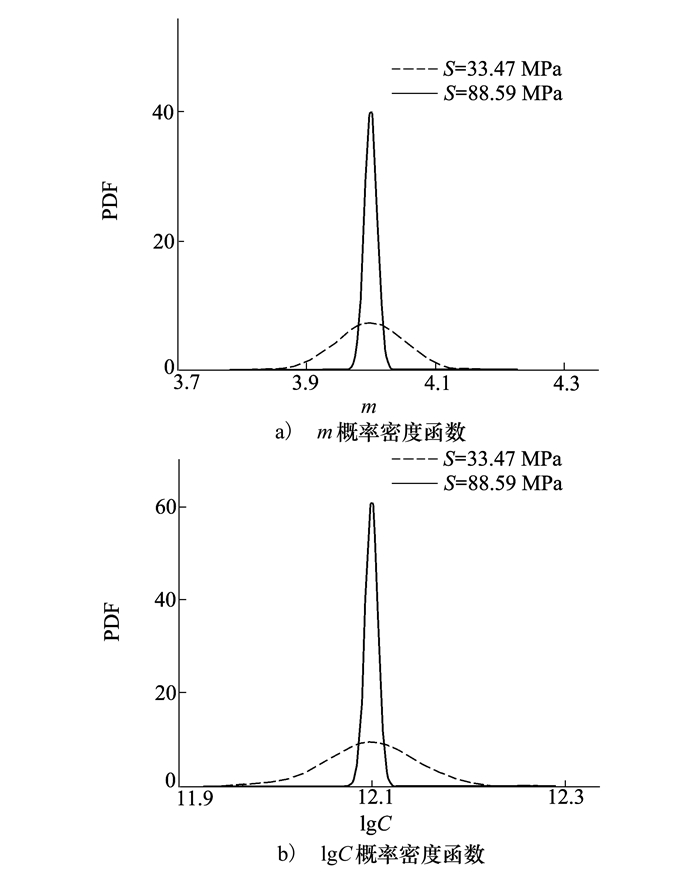
由表 3可知, m和lgC的均值在2个应力水平下基本相同, 标准差随着应力幅值增加而减小, 相关系数随应力幅值变化, 且随应力幅值增加由负相关变为正相关。这2个应力水平下的m和lgC的概率密度函数如图 3所示。
|
| 图 3 A组和C组应力水平下m和lgC的概率密度函数 |
在获得m和lgC概率分布的基础上, 对其进行随机抽样, 将抽样值反代入(10)式中获得疲劳寿命N的样本, 继而获得其统计特性, 结果列于表 4。
结合表 2和表 4可知, 由NIPC展开法预测的对数疲劳寿命的均值和标准差均落在由Bootstrap获得的对应的95%区间估计中, 且如图 4所示, 各组的试验数据也均落在NIPC预测的疲劳寿命的上下95%分位数区间内, 初步验证了上述算法在小样本情况下预测概率疲劳寿命的可行性。

|
| 图 4 A组和C组试验数据及NIPC预测的疲劳寿命分布 |
由于m和lgC的均值不随应力水平变化, 仅拟合m和lgC的标准差σ及其相关系数ρ与应力水平的关系, 如(24)式所示。
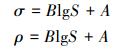
|
(24) |
由(24)式预测B组应力水平下m和lgC的标准差及其相关系数, 得到m和lgC的标准差分别为0.033 7和0.026 0, 相关系数为-0.272 3。由于此结果与实际情况可能存在偏差, 因此通过B组中3个试验数据运用贝叶斯更新对其进行修正, 结果如表 6所示。
结合表 6的数据, 对(24)式的拟合系数进行修正, 结果列于表 7, 由线性拟合相关系数R的计算值可以看出, 本文采用线性拟合是恰当的, B组试验数据均落在由此预测的疲劳寿命的上下95%分位数区间内, 如图 5所示。
| 参数 | lgC的标准差 | m的标准差 | ρ |
| B | -0.086 8 | -0.105 2 | 3.094 3 |
| A | 0.174 8 | 0.213 6 | -5.628 7 |
| R | -0.997 0 | -0.996 0 | 0.997 0 |

|
| 图 5 B组试验数据及NIPC预测的疲劳寿命分布 |
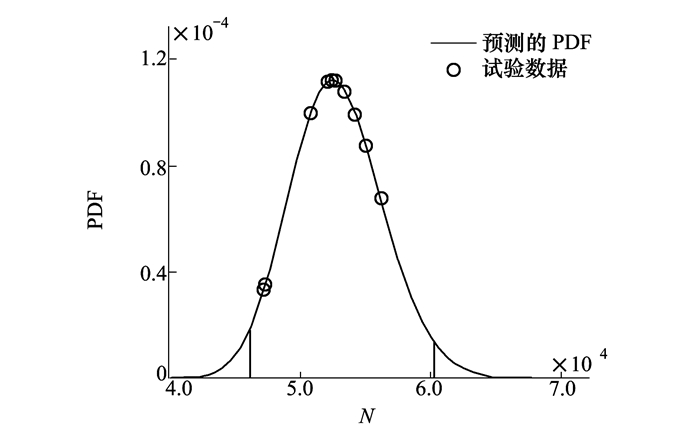
表 7中给出的修正拟合系数, 可进一步用于预测任意应力水平下的m和lgC的标准差及其相关系数, 进而用于预测该应力水平下的概率疲劳寿命。对于D组试验, 将其应力幅值70.97 MPa代入(24)式即可获得lgC的标准差为0.014 1, m的标准差为0.018 9, 相关系数为0.099 1。再对m和lgC进行随机抽样, 将抽样值代入(10)式获得疲劳寿命的样本值, 进而统计可得对数疲劳寿命的均值为4.781 7, 标准差为0.026 5, 与通过试验数据统计的概率特性对比如表 8所示, 均落在由Bootstrap获得的对应的95%区间估计内。且D组试验数据均落在预测的疲劳寿命的上下95%分位数区间内, 如图 6所示, 说明了由此预测D组的概率疲劳寿命是合理的。
|
| 图 6 D组试验数据及NIPC预测的疲劳寿命分布 |
综上可知, 在工程应用中, 在高低载2个应力水平下, 各做4个试验件, 对m和lgC的标准差及其相关系数关于应力幅值拟合, 在中间应力水平下做3个试验件, 对m和lgC的统计特征值进行贝叶斯修正并重新拟合与应力幅值的关系。在此基础上即可预测任意应力幅值下疲劳寿命的分布。因此, 仅需3个应力水平下11个试验数据, 即可完成中等寿命区p-S-N曲线的预测。通过对D组疲劳寿命的预测, 也进一步说明了此方法的合理性。
4 结论1) 在非嵌入多项式混沌展开法的基础上,将应力-寿命模型中的参数概率化,应用少量疲劳寿命样本数据可以有效预测金属材料中等寿命区的p-S-N曲线及疲劳寿命概率分布。
2) 利用本文方法对铝合金带孔板的疲劳寿命进行了预估,试验疲劳寿命均处于预测疲劳寿命分布的95%分位数区间内,表明了该方法的有效性。
| [1] |
吕媛波, 卓轶, 张文东. 齿轮接触疲劳累积损伤的概率模型[J]. 机械强度, 2017, 39(4): 957-960.
Lü Yuanbo, Zhuo Yi, Zhang Wendong. The Fatigue Cumulative Damage Probability Model of Gear Contact[J]. Journal of Mechanical Strength, 2017, 39(4): 957-960. (in Chinese) |
| [2] |
马玉娥, 王博, 熊晓枫. 玻璃纤维铝合金层板(FMLs)的疲劳损伤特性及S-N曲线[J]. 西北工业大学学报, 2016, 34(2): 222-226.
Ma Yu'e, Wang Bo, Xiong Xiaofeng. Experimental Study of Fatigue Damage of Glass-Fiber Reinforced Aluminum Laminates (FMLs)[J]. Journal of Northwestern Polytechnical University, 2016, 34(2): 222-226. (in Chinese) |
| [3] |
何朝明, 赵永翔, 杨冰, 等. LZ50车轴钢随机S-N关系的概率模型[J]. 工程力学, 2005, 22(2): 200-205.
He Zhaoming, Zhao Yongxiang, Yang Bing, et al. Probabilistic Models for the Random Fatigue S-N Relations of LZ50 Axle Steel[J]. Engineering Mechanics, 2005, 22(2): 200-205. (in Chinese) DOI:10.3969/j.issn.1000-4750.2005.02.036 |
| [4] |
李洪双, 吕震宙. 估计疲劳寿命三参数P-S-N曲线的新方法[J]. 机械强度, 2007, 29(2): 300-304.
Li Hongshuang, Lü Zhenzhou. New Method for Estimating Fatigue Life Three-Parameter P-S-N Curves[J]. Journal of Mechanical Strength, 2007, 29(2): 300-304. (in Chinese) DOI:10.3321/j.issn:1001-9669.2007.02.025 |
| [5] |
张冰, 陈立伟, 陈永祥, 等. 小子样测定叶片S-N曲线试验方法研究[J]. 中国测试, 2015, 41(12).
Zhang Bing, Chen Liwei, Chen Yongxiang, et al. Studies on Small Sample Test Method for Blade S-N Curve[J]. China Measurement & Test, 2015, 41(12). (in Chinese) |
| [6] | Ghanem R, Spanos P D. Polynomial Chaos in Stochastic Finite Elements[J]. Journal of Applied Mechanics, 2014, 57: 197-202. |
| [7] |
刘益智, 王晓东, 康顺. 多元多项式混沌方法在随机方腔流动模拟中的应用[J]. 工程热物理学报, 2012, 33(3): 419-422.
Liu Yizhi, Wang Xiaodong, Kang Shun. Applieation of Multi-Dimensional Polynomial Chaos on Numerieal Simulations of Stochastic Cavity Flow[J]. Journal of Engineering Thermophysics, 2012, 33(3): 419-422. (in Chinese) |
| [8] | Stephens M A. EDF Statistics for Goodness of Fit and Some Comparisons[J]. Journal of the American Statistical Association, 1974, 69(347): 730-737. DOI:10.1080/01621459.1974.10480196 |


