2. 兰州理工大学 理学院, 甘肃 兰州 730050
重要度理论是系统可靠性理论的重要分支。重要度在系统设计阶段主要用于发现系统薄弱环节, 为系统可靠性设计方案优化提供依据; 在系统运行阶段, 重要度主要用以系统维修资源分配和优化, 从而达到降低系统运行风险的目的。在1969年Birnbaum[1]首次提出重要度概念的基础上, 国内外学者先后提出了Barlow-Proscha重要度[2]、Fussell-Vesely重要度[3-4]、Reliability Achievement Worth[5]、Reliability Reduction Worth[6]、关键重要度[7]、冗余重要度[8]、贝叶斯重要度[9]以及综合重要度[10-12]等重要度概念。
网络是由节点和边构成的一种以图形式存在的数学模型, 其已经成为计算机通讯、交通运输、人际关系以及输变电等系统建模的主要工具。网络中一些特殊的节点称为终端节点, 网络的可靠性一般定义为网络所有终端节点之间连通的概率。1994年Page和Perry[13]提出了link重要度、contract-delete重要度。其中link重要度量化了一条边的故障对整个网络可靠性的影响程度; contract-delete重要度分析了包含目标边的最小割集(路集)的大小和数目等对网络可靠性的影响程度。Gertsbakh和Shpungin[14]利用Birnbaum重要度, 评估了一条边状态改变对网络可靠性的影响程度, 并采用Fussell-Vesely重要度量化了一条边的故障引起网络可靠性的衰减程度。Hong和Lie[15]提出了2条边的联合重要度, 分析了2条边状态同时改变对网络可靠性的影响程度, 拓展了单条边的Birnbaum重要度概念。针对一个中等或者大型网络边的重要度计算问题, Gertsbakh和Shpungin提出了一种基于网络结构谱-D谱的蒙特卡罗模拟方法, 给出了网络边的Birnbaum、Fussell-Vesely、联合重要度[14, 16]计算模型。Hsu和Yuang[17]提出了一种两阶段算法, 以此计算网络边的Birnbaum重要度。
传统的网络边重要度计算主要依赖于边的可靠性和网络结构。但在实际工程中, 边的故障个数及其分布是易获得的统计数据信息, 据此考察网络边的重要度对于网络薄弱环节及可靠性优化更具有实际意义。本文利用网络结构D-谱, 重点研究网络边故障个数分布为饱和泊松分布时, 网络边的Birnbaum重要度计算方法。该方法所输入的信息仅为网络边个数故障统计信息, 方便于工程应用。
1 概率分布下的Birnbaum重要度计算方法本文考虑的K网络是一个由节点和边组成的无向图N=(V, E, K)。V为节点集合且|V|=m, E为边集合且|E|=n。一些特殊节点的集合K⊆V被称为网络的终端节点集合。本文在假设网络节点无故障的条件下, 重点研究网络边发生故障条件下的网络薄弱环节识别的方法。如果网络第i条边运行, 则xi=1, 否则xi=0。本文假设网络边的可靠性独立同分布。如果集合K中至少有一对节点之间不连通, 则称该网络处于故障状态, 记为φ(x)=0, 否则φ(x)=1。这里φ为网络的结构函数, 网络的可靠性定义为R=P(φ(x)=1)。在计算网络的可靠性及边重要度时, 网络的结构不变量:D-谱起着关键作用。
定义1 给定由n条边构成的网络, 定义网络D-谱:F(k)=P(φ=0|k条边故障), 包含边i的D-谱:F(k, 0i)=P(φ=0, xi=0|k条边故障), 和不包含边i的D-谱:F(k, 1i)=P(φ=0, xi=1|k条边故障)。
由于网络边的故障概率独立同分布, 因此F(k)、F(k, 0i)和F(k, 1i)仅依赖于给定网络的结构, 故称为结构不变量[18]。显然F(k)=F(k, 0i)+F(k, 1i)。
给定一个网络, 设其故障边的个数为随机变量X。由于网络边的故障概率独立同分布, 若已知故障个数X=k, (k=0, 1, …, n)那么
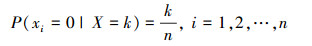
|
依据全概率公式, 网络边i的故障概率为
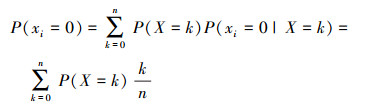
|
为了考察一条边故障或运行时, 对整个网络故障的影响程度, 需要下面的条件概率。
若已知边i故障、xi=0, 则网络的条件故障概率为

|
(1) |
若已知边i运行、xi=1, 则网络的条件故障概率为
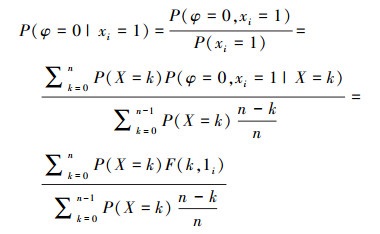
|
(2) |
当已知网络故障边个数的概率分布时, 定理1给出了网络边Birnbaum重要度的计算公式。
定理1 给定一个由n条边组成的网络, 令随机变量X为该网络边的故障个数, 则边i的Birnbaum重要度为
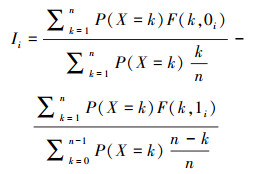
|
(3) |
证明 根据Birnbaum重要度的定义[1], 网络边i的Birnbaum重要度为:
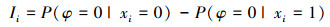
|
(4) |
将(1)式和(2)式代入Birnbaum定义(4),即得(3)式。 证毕。
2 饱和泊松分布下的Birnbaum重要度一般泊松分布的概率质量函数为P(X=k)=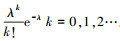

|
(5) |
因此, 网络边i的Birnbaum重要度计算公式为:
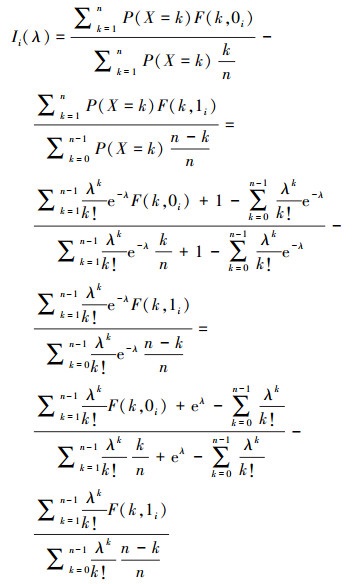
|
(6) |
定理2 给定一个由n条边组成的网络, 令随机变量X为该网络边的故障个数, 且X服从参数为λ的饱和泊松分布。那么, Ii > Ij的充分必要条件为

|
(7) |
证明 依据边i的状态, 取条件概率后得到
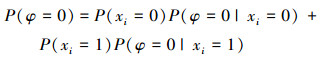
|
进而得到
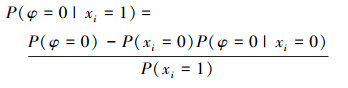
|
把上式代入Birnbaum重要度的定义中, 得到

|
同理

|
因为边的可靠性独立同分布, P(xi=0)=P(xj=0), P(xi=1)=P(xj=1)。所以Ii > Ij当且仅当
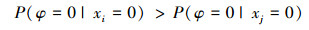
|
根据(1)式和(5)式, 上式等价于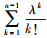
定理2说明了在网络边故障个数服从饱和泊松分布条件下, 网络边的Birnbaum重要度的排序, 不但取决于网络结构(即F(k, 0i)和F(k, 0j)), 而且依赖于故障边个数分布的参数λ。
推论1 给定一个由n条边组成的网络, 令随机变量X为该网络边的故障个数, 且X服从参数为λ的饱和泊松分布。那么当λ→0时, 如果F(kmin(i, j), 0i) > F(kmin(i, j), 0j), 则Ii > Ij, 其中kmin(i, j)=min{k: F(k, 0i)≠F(k, 0j)}。
证明 根据kmin(i, j)的定义和定理2, 得到Ii > Ij当且仅当
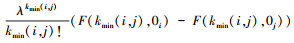
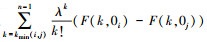
推论1说明了参数λ趋近于无穷小时, 网络边的Birnbaum重要度排序仅决定于结构因素。
3 算例图 1为一个三终端的超立方体网络H4。该网络有16个节点, 节点1、10、16为终端节点; 且有32条边, 每条边表示为(h, s), 其中h和s为该边的2个节点。假设节点不发生故障, 边的故障概率独立同分布, 网络可靠性定义为节点1、节点10和节点16彼此连通的概率。

|
| 图 1 终端节点集合为{1, 10, 16}超立方体网络H4 |
由图 1知, 网络H4的最小割集大小为4。Gertsbakh和Shpungin等人[14]设计了蒙特卡罗模拟算法来计算网络中的D-谱。表 1给出了大小分别为4、5、6的网络D-谱和前8条边的D-谱, 其排名的准则是:先比较F(4, 0i)与F(4, 0j), 若F(4, 0i)=F(4, 0j), 则比较F(5, 0i)与F(5, 0j), 以此类推。另外, 在表 1中, F(k), F(k, 0i)分别写为Fk, Fk, (h, s), 其中边i表示为(h, s)。
| k | 4 | 5 | 6 |
| Fk | 7.90×10-5 | 3.93×10-4 | 1.24×10-3 |
| Fk, (14, 16) | 3.20×10-5 | 1.40×10-4 | 4.83×10-4 |
| Fk, (8, 16) | 3.20×10-5 | 1.37×10-4 | 4.74×10-4 |
| Fk, (15, 16) | 3.20×10-5 | 1.37×10-4 | 4.63×10-4 |
| Fk, (12, 16) | 3.20×10-5 | 1.33×10-4 | 4.62×10-4 |
| Fk, (1, 5) | 2.90×10-5 | 1.42×10-4 | 4.83×10-4 |
| Fk, (1, 2) | 2.90×10-5 | 1.42×10-4 | 4.76×10-4 |
| Fk, (1, 3) | 2.90×10-5 | 1.41×10-4 | 4.71×10-4 |
| Fk, (1, 9) | 2.90×10-5 | 1.40×10-4 | 4.78×10-4 |
当λ=0.01、17、40时, 根据公式(6)、表 2分别给出了前8条边的Birnbaum重要度。由表 2知, 当λ取不同值时, 网络H4各条边的Birnbaum重要度排序完全不同。但是, 在λ=0.01、17、40的3种情况下, 前8条的边几乎都与网络H4的终端节点1、10、16相连。因此, 与终端节点相连边的状态改变, 对整个网络可靠性的影响程度较大。
| λ=0.01 | 边i | λ=17 | 边i | λ=40 | 边i |
| 1.051 477 137 6×10-10 | (14, 16) | 0.516 573 | (14, 16) | 0.027 573 | (1, 2) |
| 1.051 477 112 7×10-10 | (8, 16) | 0.516 557 | (1, 2) | 0.025 574 | (12, 16) |
| 1.051 477 112 5×10-10 | (15, 16) | 0.516 236 | (1, 9) | 0.025 528 | (1, 9) |
| 1.051 477 079 5×10-10 | (12, 16) | 0.515 646 | (12, 16) | 0.025 490 | (9, 10) |
| 1.051 464 774 6×10-10 | (1, 5) | 0.514 006 | (9, 10) | 0.025 391 | (14, 16) |
| 1.051 464 774 5×10-10 | (1, 2) | 0.513 652 | (10, 14) | 0.024 906 | (10, 14) |
| 1.051 464 766 2×10-10 | (1, 3) | 0.513 345 | (10, 12) | 0.023 912 | (13, 14) |
| 1.051 464 758 0×10-10 | (1, 9) | 0.513 214 | (2, 10) | 0.022 984 | (2, 10) |
当λ取非常小的值0.01时, 表 2给出的前8条边的排序与表 1完全相同, 该结果与推论1的结论相符合。当λ足够小时, 包含边i的非零较小的D-谱值主导着该边的Birnbaum重要度大小。
4 结论本文针对网络边重要度评估问题, 提出了一种基于饱和泊松分布的Birnbaum重要度计算方法, 讨论了影响网络边重要度排序的条件和参数, 结合具体算例给出了基于饱和泊松分布的Birnbaum重要度的应用方法。从而为网络系统可靠性的优化奠定了基础。
| [1] | Birnbaum Z W. On the Importance of Different Components in a Multicomponent System//Multivariate AnalysisⅡ[M]. Ed by Krishnaiahp R. New York, Academic Press, 1969:581-592 |
| [2] | Barlow R E, Proschan F. Importance of System Components and Fault Tree Events[J]. Stochastic Processes and Their Applications, 1975, 3(2): 153-173. DOI:10.1016/0304-4149(75)90013-7 |
| [3] | Vesely W E. A Time-Dependent Methodology for Fault Tree Evaluation[J]. Nuclear Engineering and Design, 1970, 13(2): 337-360. DOI:10.1016/0029-5493(70)90167-6 |
| [4] | Fussell J B. How to Hand-Calculate System Reliability and Safety Characteristics[J]. IEEE Trans on Reliability, 1975, 24(3): 169-174. |
| [5] | Vasseur D, Llory M. International Survey on Psa Figures of Merit[J]. Reliability Engineering & System Safety, 1999, 66(3): 261-274. |
| [6] | Levitin G, Podofillini L, Zio E. Generalised Importance Measures for Multi-State Elements Based on Performance Level Restrictions[J]. Reliability Engineering & System Safety, 2003, 82(3): 287-298. |
| [7] | Kuo W, Zuo M J. Optimal Reliability Modeling:Principles and Applications[M]. New York: John Wiley &Sons, 2003. |
| [8] | Shen K, Xie M. On the Increase of System Reliability by Parallel Redundancy[J]. IEEE Trans on Reliability, 1990, 39(5): 607-611. DOI:10.1109/24.61320 |
| [9] | Singpurwalla N D. Reliability and Risk:A Bayesian Perspective[M]. New York: Join Wiley & Sons, 2006. |
| [10] |
司书宾, 杨柳, 蔡志强, 等. 二态系统组(部)件综合重要度计算方法研究[J]. 西北工业大学学报, 2011, 29(06): 939-947.
Si Shubin, Yang Liu, Cai Zhiqiang, et al. A New and Eficient Computation Method of Im (Integrated Importance Measures) for Components in Binary Coherent Systems[J]. Journal of Northwestern Polytechnical University, 2011, 29(6): 939-947. (in Chinese) |
| [11] | Si S B, Dui H Y, Cai Z Q, et al. Joint Integrated Importance Measure for Multi-State Transition Systems[J]. Communications in Statistics-Theory and Methods, 2012, 41(21): 3846-3862. DOI:10.1080/03610926.2012.688158 |
| [12] |
涂慧玲, 张胜贵, 司书宾, 等. 面向维修过程的多态混联系统综合重要度计算方法[J]. 自动化学报, 2014, 40(01): 126-134.
Tu Huiling, Zhang Shenggui, Si Shubin, et al. The Integrated Importance Measure of Multi-State Compound Systems for Maintenance Processes[J]. Acta Automatica Sinica, 2014, 40(1): 126-134. (in Chinese) |
| [13] | Page L B, Perry J E. Reliability Polynomials and Link Importance in Networks[J]. IEEE Trans on Reliability, 1994, 43(1): 51-58. DOI:10.1109/24.285108 |
| [14] | Gertsbakh I, Shpungin Y. Network Reliability Importance Measures:Combinatories and Monte Carlo Based Computations[J]. WSEAS Transactions on Computers, 2008, 7(4): 216-227. |
| [15] | Hong J S, Lie C H. Joint Reliability-Importance of Two Edges in an Undirected Network[J]. IEEE Trans on Reliability, 1993, 42(1): 17-23. DOI:10.1109/24.210266 |
| [16] | Gertsbakh I B, Shpungin Y. Combinatorial Approach to Computing Component Importance Indexes in Coherent Systems[J]. Probability in the Engineering and Informational Sciences, 2012, 26(1): 117-128. DOI:10.1017/S026996481100026X |
| [17] | Hsu S J, Yuang M C. Efficient Computation of Marginal Reliability Importance for Reducible Networks in Network Management[C]//Proceedings of the 1999 IEEE International Conference on Communications, 1999:1039-1045 |
| [18] | Vaisman R, Kroese D P, Gertsbakh I B. Improved Sampling Plans for Combinatorial Invariants of Coherent Systems[J]. IEEE Trans on Reliability, 2016, 65(1): 410-424. DOI:10.1109/TR.2015.2446471 |
| [19] | Kim J, Dobson I. Approximating a Loading-Dependent Cascading Failure Model with a Branching Process[J]. IEEE Trans on Reliability, 2010, 59(4): 691-699. DOI:10.1109/TR.2010.2055928 |
2. School of Science, Lanzhou University of Technology, Lanzhou 730050, China



