机构的自由度分析是机构学最基本的问题,其目的不仅要确定实现机构输出运动所需要的最少输入的数目,而且要确定机构输出的运动类型,即转动或移动。瞬时自由度是对一定位型下的机构直接从分析其约束关系而导出的自由度。正方形单元机构[1-3]的自由度发生瞬时变化时,机构的各项运动性能均会恶化,导致机构运动失控和系统失稳等,甚至会导致重大安全事故发生。同时也可利用瞬时自由度实现机构的增力、锁止等功能,因此研究正方形单元机构瞬时自由度使机构在设计阶段避免出现瞬时自由度或快速越过瞬时自由度位置,达到机构运动可控的目的;对利用瞬时自由度位置进行工作的锁机构、夹持机构和定位机构等保证在工作中可靠地进入瞬时自由度位置,具有十分重要的科学意义。因此,瞬时自由度分析已经成为近几年机构学研究的热点问题之一。
由于瞬时自由度是通过分析在特定位型下的约束关系而导出的,瞬时自由度是依赖对应的位型。当机构的位型发生变化时,机构的自由度数目或性质中就有一个随之变化。具有瞬时自由度的机构是不稳定的,并随着机构的位型变化而变化。传统上一般应用Grübler-Kutzbach(G-K)公式对机构自由度进行分析,G-K公式仅仅考虑机构的构件数目、运动副数目和类型,用最简单的算术解决了机构的自由度计算问题。许许多多的机构用这个经典的公式得到了正确的结果,包括绝大多数的平面机构和少数的空间机构。但是,G-K公式无法对机构的瞬时自由度进行分析,因此许多学者不断探索解决自由度分析的新方法。
1978年Hunt建立了多环机构自由度计算公式,但该公式无法识别合适的独立环和赋值系数。1978年Hervé首次运用位移集构成的群结构来分析自由度。2005年法国学者Gogu回顾了过去150多年自由度的计算方法,研究分析了35种自由度公式的产生、局限性和相似性,并把这些公式分为两类,一类是基于约束方程和秩的求解方法,另一类是不需要约束方程的快速计算自由度的方法[4-7]。并强调了运用快速计算自由度方法不适合多数古典机构和现代并联机构。
随着螺旋理论的不断发展和应用,为解决过约束机构的自由度计算等问题,提供了一个强有力的数学工具。陈巧红等[8]基于螺旋理论分析了3-PRRRR并联机构的自由度和约束奇异性。于靖军等[9]提出了基于反螺旋理论对一类两自由度并行机构自由度和奇异性分析的视图图形方法。赵景山等[10]提出了基于螺旋理论的机构学的自由度的分析计算方法,奇异性和稳定性的构型自由度概念;随后,赵景山等[11]基于反螺旋理论对空间并行机构的构型进行了自由度计算。黄真等[12-13]基于反螺旋理论研究了并联机构的多分支闭合所产生的过约束。Rico等[14]基于李代数的理论提出了过约束机构的计算自由度方法。但是,只有少数论文提出了对正方形单元组合机构瞬时自由度的研究方法。
正方形单元组合机构作为一类具有复杂几何形状的结构,它不仅含有大量冗余约束的多闭环结构,而且还是一个串并联结构[15-16]。如果采用传统的自由度计算公式,求解瞬时自由度相当复杂,冗余约束数目难以确定,常常产生错误的结果。本文提出一种基于螺旋理论和图论相结合的方法求解正方形单元组合机构的瞬时自由度。
1 螺旋理论基础螺旋理论分析机构特别方便,它具有几何概念清楚,物理意义丰富,表达形式简单,数学运算方便,理论难度较低等优点,在机构学中得到广泛应用。
1.1 螺旋量螺旋量是含旋矩的线矢量,为几何量,也是李代数中通过原点的射线,是射影李代数的元素。
螺旋量是一个几何体,可用一对三维向量构成的六维向量表示如下:
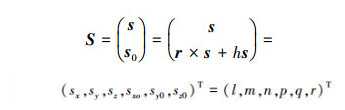
|
(1) |
式中, S是方向向量表示的螺旋量轴线。螺旋量的代数形式包括两部分, 螺旋量的轴线向量S=(sx, sy, sz)T为主部, 也称作原部。用于确定轴线位置与旋矩的向量So=(sxo, syo, szo)T为副部, 也称作对偶部。螺旋量由Plücher坐标在空间定义的线矢量构成和延伸, 包括沿线矢量的向量、该线矢量的矢矩以及螺距。简而言之, 螺旋量即具有旋矩的线矢量。一般为单位线矢量加上螺距, 实际工程应用中考虑带幅值的非单位螺旋量, 包括速度螺旋量和力螺旋量。
1.2 螺旋运算螺旋量和其他代数量一样, 遵循一定的运算规则。螺旋量包括主部和副部, 螺旋的原部指螺旋的轴线方向向量, 其对偶部指的是确定螺旋的位置和螺距。
螺旋量的数乘。实数和螺旋的乘法称为螺旋的数乘。λ乘以(1)得:
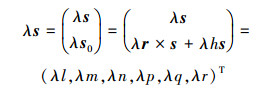
|
(2) |
两螺旋量的代数和。两螺旋量分别为S1=(s1; s1o), S2=(s2; s2o), 两螺旋的代数和仍为螺旋量, 且螺旋的主部和副部分别为两螺旋的主部和副部之和。
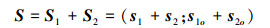
|
(3) |
两螺旋量的互矩成为螺旋量的互易积, 也称为螺旋量的标量积。

|
(4) |
两螺旋量的叉积, 两螺旋量分别为S1=(s1; s1o), S2=(s2; s2o), 两螺旋量的叉积由螺旋量主部的叉积及其相对应主、副部交叉的叉积得到的向量构成, 表示为:
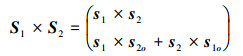
|
(5) |
把螺旋理论引入正方形单元组合机构中, 为解决多环过约束机构的瞬时自由度计算问题, 提供了一个强有力的数学工具。
2 瞬时自由度模型的建立以正方形单元机构和正方形单元组合机构为研究对象, 运用图论和螺旋理论相结合, 绘制出正方形单元组合机构的拓扑图, 从而分析机构的瞬时自由度。
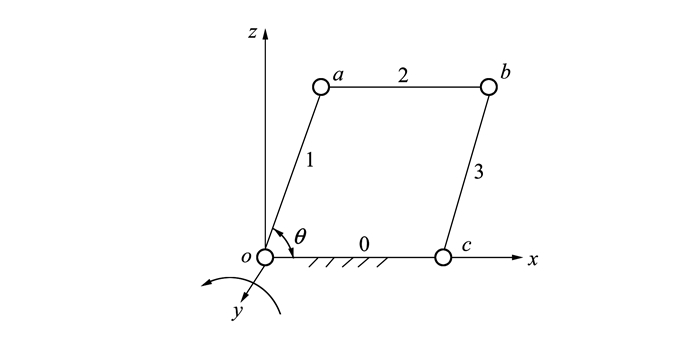
2.1 正方形单元机构根据正方形单元机构的几何特性, 建立其空间笛卡尔坐标系, 如图 2所示,
|
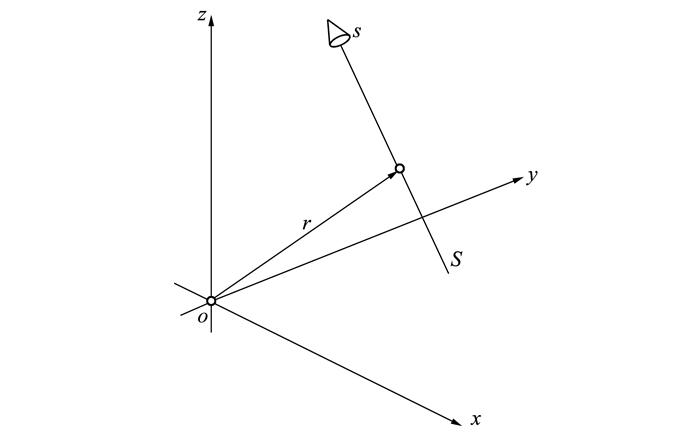
| 图 1 螺旋轴线及其位置向量 |
|
| 图 2 正方形单元机构的坐标系 |
用阿拉伯数字对杆件进行编号, 用小写字母对转动副编号, 正方形单元机构的轴线相互平行, 4个转动副表示成螺旋, 选取所有螺旋沿转动副轴线沿y轴, 假定每个杆件长度为l, 杆件1与x轴的夹角为θ, 则在图 2中各个运动副的位置为:

|
(6) |
各个运动副方向为:
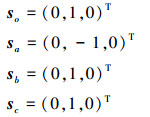
|
(7) |
根据螺旋理论可得各个运动副的螺旋量:
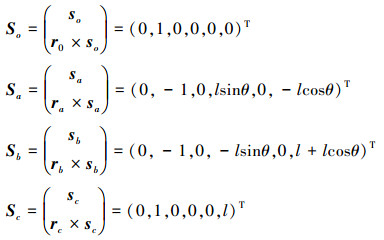
|
(8) |
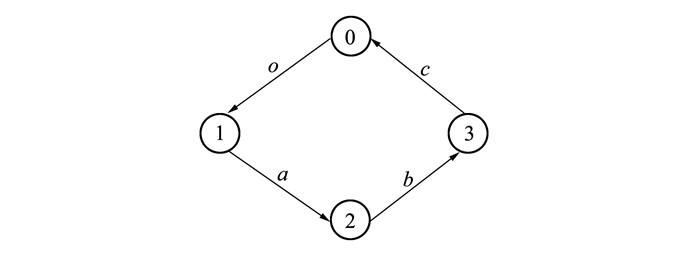
根据图论, 用线条表示相应的运动副, 用圆圈表示相应的杆件, 可得正方形单元机构的约束机构拓扑图, 如图 3所示。
|
| 图 3 正方形单元机构约束拓扑图 |
依据图 3所示拓扑图, 建立相应的约束螺旋方程:
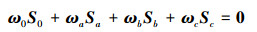
|
(9) |
式中, ωp是转动副p的角速度量, Sp是相应的螺旋量, 写成矩阵形式:
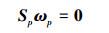
|
(10) |
式中
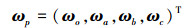
|
(11) |
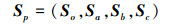
|
(12) |
带入各螺旋量可得Sp的秩r(Sp), 通过MATLAB仿真求解得到正方形单元螺旋约束方程的秩如图 4所示。
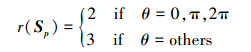
|
(13) |
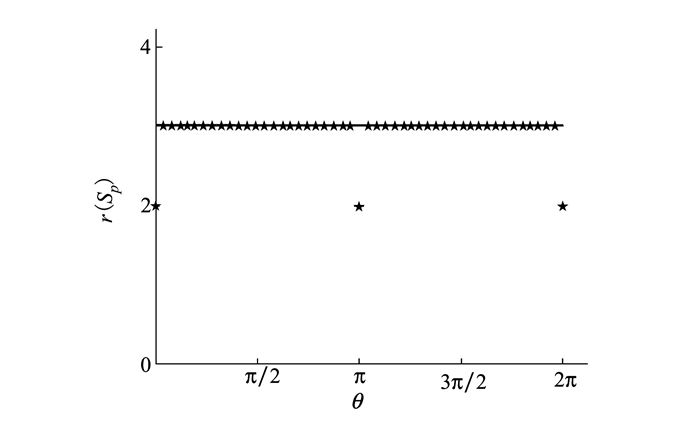
|
| 图 4 正方形单元机构螺旋约束方程的秩 |
从而可以得知, 由于约束矩阵的维数是4, 当θ=0, π, 2π时, 该机构的瞬时自由度:
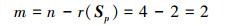
|
(14) |
当瞬时自由度m=2时, 机构处于奇异位型。如图 5所示。

|
| 图 5 正方形单元机构的奇异位置 |
当正方形单元机构发生转动后, 杆1与x轴的夹角是θ, 铰接点a在oxz坐标系内的位置为pa=(lcosθ, lsinθ)T, 当θ=0, π, 2π时
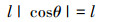
|
(15) |
转动自由度m是瞬时的, 杆1不能实现真正转动。为了使正方形单元机构正常工作, 采用摄动理论, 在θ上增加一个缓慢变化的参数Δθ, (15)式则不成立, 机构实现转动以正常工作。
由于约束矩阵的维数是4, 当约束矩阵的秩等于3时, 正方形单元机构的自由度:
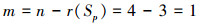
|
(16) |
只有当正方形单元机构处于非奇异位型时, 机构才能正常工作。
以图 2为例, 用传统的G-K公式计算正方形单元机构的自由度:

|
(17) |
可以看出由G-K公式得到的自由度始终为1, 但是实际的运动过程中有一些特殊的位置, 例如在0、π、2π时正方形单元机构运动是不稳定的, 因此该机构的瞬时自由度在这些位置不为1, 故传统的G-K公式不能正确反映这些位置的瞬时自由度。
文献[12]对传统的G-K公式进行了改进, 引入了过约束的概念:
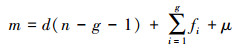
|
(18) |
式中,μ表示机构中过约束的总数。根据文献[12]的思路, 分析可得:
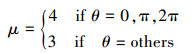
|
(19) |
将μ带入(18)式, 可得:
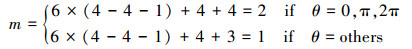
|
(20) |
计算结果验证了本文所提方法的正确性。一般来说, 简单机构的过约束容易确定, 但是大型复杂的可展机构过约束是难以确定的, 而本文的方法不需要求过约束数, 因此在一定程度上提高了复杂机构自由度的计算效率。
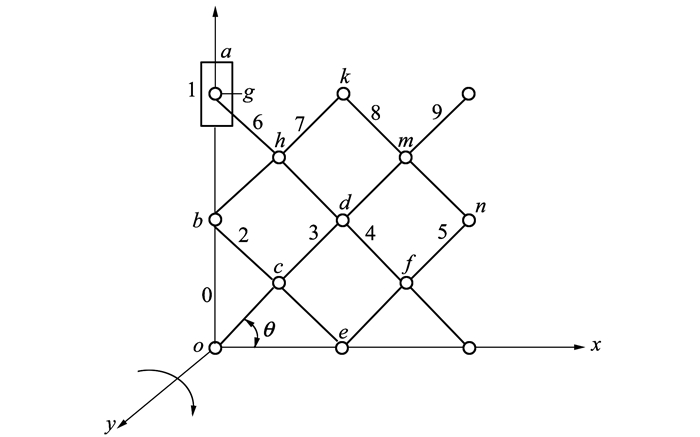
2.2 正方形单元组合机构根据正方形单元组合机构的几何特性, 建立其空间笛卡尔坐标系, 如图 6所示, 假定每个杆件长度为l, 杆件3与x轴的夹角为θ, 则在图 6中各个运动副的位置为:
|
| 图 6 正方形单元组合机构的坐标系 |
杆件编号为:0(机架)、1、2、3、4、5、6、7、8、9。
运动副编号:o、a、b、c、d、e、f、g、h、k、m、n。运动副中只有a是移动副, 其他运动副都是转动副。
根据正方形单元组合机构的几何关系和螺旋理论, 各运动副的位置如下:
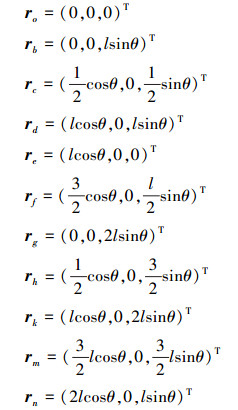
|
(21) |
各个运动副的方向如下:

|
(22) |

|
| 图 7 正方形单元组合机构的约束拓扑图 |
根据图 7中正方形单元组合机构的约束关系, 得整个闭环单元正方形单元组合机构的螺旋方程为:
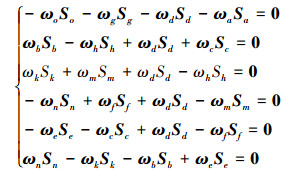
|
(23) |
式中, ωp表示运动副p的角速度量。0是6维列向量。将(19)式写出矩阵的形式为:
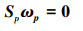
|
(24) |
式中
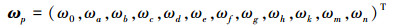
|
(25) |
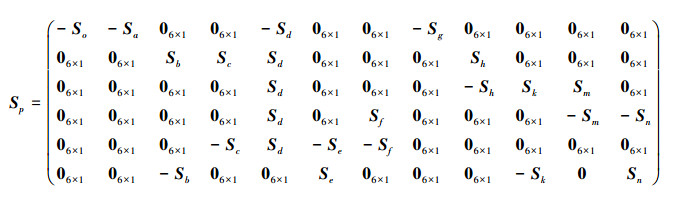
|
(26) |
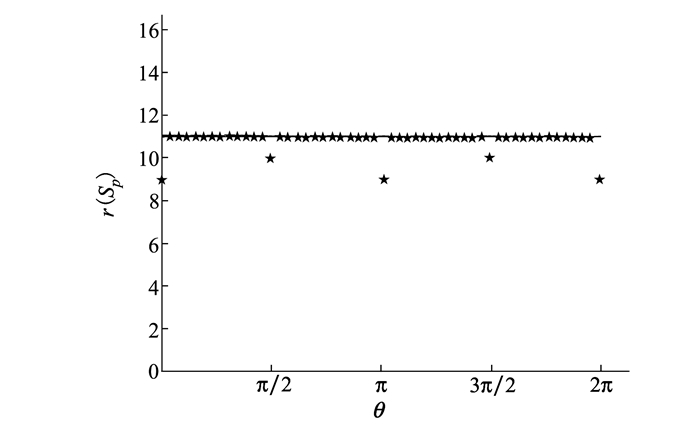
带入各螺旋量可得Sp的秩r(Sp), 通过MATLAB仿真求解可得正方形单元螺旋约束方程的秩如图 8所示。
|
| 图 8 正方形组合机构螺旋约束方程的秩 |
由图 8可得:
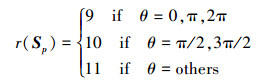
|
(27) |
由于约束矩阵的维数是12, 从而可以得知, 当θ=0, π, 2π时, 约束矩阵的秩r(Sp)=9, 该机构瞬时自由度为:

|
(28) |
当θ=π/2, 3π/2时, r(Sp)=10, 该机构瞬时自由度为:
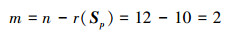
|
(29) |
当正方形单元组合机构运动时, 转动自由度m=3, m=2是瞬时的, 正方形单元组合结构中的杆就不能实现真正转动。为了使正方形单元机构正常工作, 采用摄动理论, 在θ上增加一个缓慢变化的参数Δθ, 机构实现转动以正常工作。
当约束矩阵的秩等于11时, 正方形单元组合机构的自由度是:
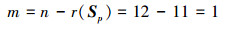
|
(30) |
只有当正方形单元组合机构处于非奇异时,自由度才是正确的。
由以上分析可知,当机构处于奇异位型时,机构的自由度数目瞬时发生变化,导致不能继续运动或者失去运动确定性与稳定性。另外,对于传递动力的机构,奇异位型下还会出现受力状态变坏,各构件角速度和铰链点加速度发生突变,会产生较大的冲击和振动。对于在轨工作航天器,这种冲击和振动往往会与航天器的在轨运动耦合,影响航天器的在轨姿态,引起致命的后果,尤其对于通信卫星,航天器在轨姿态的改变会影响卫星天线的姿态,影响通信质量,甚至造成通信卫星的失效。反过来,也可利用机构的奇异特性实现增力、锁死等功能。
把正方形单元机构和正方形单元组合机构组合成的复杂的多闭环机构,运用图论和螺旋理论分析计算出其瞬时自由度,并进行了MATLAB仿真验证,证明了文中提出的方法切实可行。
3 结论1) 基于图论法得到了正方形单元机构约束拓扑图,并结合螺旋理论建立了正方形单元机构的瞬时自由度计算方法。克服了传统的G-K公式无法求解机构特殊位置瞬时自由度的缺点,更能反映机构运动过程中的真实自由度。采用修正的G-K公式验证本文提出方法的正确性,本文方法通过约束方程求秩得到了机构的瞬时自由度,避免了修正G-K公式求解过约束的过程,并且将其应用到正方形组合可展机构自由度分析,求解效率更高。
2) 机构在特殊位置出现的瞬时自由度,会引起运动的不稳定。为了解决这一问题,引入了摄动理论,在机构出现瞬时多自由度位置,增加一个或多个作缓慢变化的参数,避开或快速越过瞬时自由度,使机构正常工作。
3) 本文建立的正方形单元组合机构瞬时自由度的分析模型和方法,为解决该类结构瞬时自由度计算问题,提供了一种有效切实可行的途径,为其运动控制奠定了基础。
| [1] | Phillips J. Freedom in Machinery[M]. Sydney: Cambridge University Press, 1990. |
| [2] | Pellegrino S. Deployable Structures[M]. New York: Springer, 2001. |
| [3] | Li J, Wang S, Zhi C, et al. Configuration Design and Kinematics Research of Scissor Unit Deployable Mechanism[M]. Mechanism and Machine Science Springer Singapore, 2017 http://link.springer.com/10.1007/978-981-10-2875-5_62 |
| [4] | Gantes C J. Deployable Structures:Analysis and Design[M]. Southampton: England:Wit Press, 2001. |
| [5] | Escrig F, Brebbia C A. Mobile and Rapidly Assembled StructuresⅡ[M]. Southampton, UK: Computational and Mechanics Publications, 1996. |
| [6] | Hervé J M. Analyse Structurelle Des Mécanismes Par Groupe Des Déplacements[J]. Mechanism & Machine Theory, 1978, 13(4): 437-450. |
| [7] | Gogu G. Mobility of Mechanisms:a Critical Review[J]. Mechanism & Machine Theory, 2005, 40(9): 1068-1097. |
| [8] | Chen Q, Qinchuan L I, Chuanyu W U. Mobility, Constraint Singularity and Isotropy of the 3-PRRRR Translational Parallel Mechanism[J]. Chinese Journal of Mechanical Engineering, 2009, 22(6): 841-848. DOI:10.3901/CJME.2009.06.841 |
| [9] | Yu J J, Dong X, Pei X U, et al. Mobility and Singularity Analysis of a Class of Two Degrees of Freedom Rotational Parallel Mechanisms Using a Visual Graphic Approach[J]. Journal of Mechanisms & Robotics, 2012, 4(4): 61-68. |
| [10] | Zhao J S, Zhou K, Feng Z J. A Theory of Degrees of Freedom for Mechanisms[J]. Mechanism & Machine Theory, 2004, 39(6): 621-643. |
| [11] | Zhao J S, Feng Z J, Dong J X. Computation of the Configuration Degree of Freedom of a Spatial Parallel Mechanism by Using Reciprocal Screw Theory[J]. Mechanism & Machine Theory, 2006, 41(12): 1486-1504. |
| [12] | Huang Z, Tao W S, Fang Y F. Study on the Kinematic Characteristics of 3 DOF In-Parallel Actuated Platform Mechanisms[J]. Mechanism & Machine Theory, 1996, 31(8): 999-1007. |
| [13] | Huang Z, Xi F, Huang T, et al. Lower-Mobility Parallel Robots:Theory and Applications[J]. Advances in Mechanical Engineering, 2010, 2(2): 1652-1660. |
| [14] | Rico J M, Ravani B. On Calculating the Degrees of Freedom or Mobility of Overconstrained Linkages:SingleLoop Exceptional Linkages[J]. Journal of Mechanical Design, 2007, 129(3): 15-9. |
| [15] | Zhao Y, Liu J F, Huang Z. A Force Analysis of a 3-Rps Parallel Mechanism by Using Screw Theory[J]. Robotica, 2011, 29(7): 959-965. DOI:10.1017/S0263574711000129 |
| [16] | Chen Yan, You Zhong, Tarnai T. Three Fold-Symmetric Bricard Linkages for Deployable Structures[J]. International Journal of Solids and Structures, 2005, 42(8): 2287-2230. DOI:10.1016/j.ijsolstr.2004.09.014 |


