在系统随机不确定性分析与设计研究领域, 为全面衡量输入变量对输出参数性能的影响, 众多学者进行了大量的学术与工程应用研究, 建立了以重要性测度(重要度)来衡量这种影响的理论体系[1]。而重要度(灵敏度)分析又可以分为局部重要度分析和全局重要度分析。局部重要度定义为输入变量分布参数的变化引起输出性能统计特征变化的比率[2]。这一比率可以用输出性能统计特征对分布参数的偏导数来描述, 对此, 已有很多国内外学者进行了细致的研究。但是局部重要度存在明显的局限性, 即只能反映输入变量在名义值处对输出性能统计特征的影响, 而不能反映输入变量的完整不确定性对输出性能统计特征的影响。而全局重要度分析可以从输入变量的整个分布范围来衡量其不确定性对我们所感兴趣的输出统计特征的影响[1]。
在全局重要度研究领域, Iman和Hora[3]于1990年提出了理想的重要性测度指标的计算方法, 但是该方法需要同时求解三种不同的重要度指标, 计算量大。Sobol[4]于1993年建立了一系列基于方差的基本变量重要性测度指标。Saltelli等[5]在Sobol重要性测度指标的基础上总结出基本变量重要性测度指标的要求, 即“全局性, 可量化性, 通用性”, 并提出了相应的指标。此外, Homma和Saltelli[6]还引入了总效应指标表征变量自身及其与其他变量相互作用对输出性能指标方差的影响, 并给出有效的计算方法[7]。
失效概率是不确定性系统的一种重要性能指标, 而基于失效概率的全局重要度研究还未全面展开, 研究成果较少。Li和Lu等[8]提出了基于失效概率的全局重要度, 并推导了其与基于方差的重要度指标之间的关系, 为可靠性评估与全局重要性测度分析建立了新的桥梁。基本变量对失效概率的重要性测度的求解涉及到无条件失效概率和有条件失效概率的计算对于求解失效概率, 通常有近似解析法和数字模拟法[9]。近似模拟法包括一次二阶矩法和改进的一次二阶矩法等, 而数字模拟法的经典代表就是直接蒙特卡罗法(Monte Carlo, MC)。由于数字模拟法在失效概率评估和重要度分析上具有较好的相容性, 因此在基于失效概率的全局重要度研究中, 数字模拟法更为通用。李贵杰等[10]建立了鞍点线抽样方法。Wei和Lu等[11]给出了3种计算基于失效概率的全局重要度的数字模拟法, 包括直接蒙特卡罗法、重要抽样法(importance sampling, IS)和截断重要抽样法(truncated importance sampling, TIS)。Cheng等人研究了拒绝抽样技术在基于失效概率的全局重要度分析中应用[12]。对比而言, 重要抽样法和截断重要抽样法的计算效率较高, 但是存在设计点位置及个数难以确定的困难, 进一步引起重要抽样函数选择困难, 降低了其应用范围。
交叉熵方法是一种重要抽样法, 其本质是对重要抽样函数选择过程的改进, 可以部分避免确定设计点位及个数。因此本文将建立求解基本变量对失效概率影响的重要性测度评估的交叉熵方法, 并对所建立方法进行计算精度和效率方面的验证, 为失效概率重要性测度评估提供一种新的可选方法。
1 基于失效概率的全局重要性测度在包含n维不确定性变量的可靠性模型Y=g(x)=g(x1, x2, …, xn)中, x=[x1, x2, …, xn]T为基本输入随机变量, g(x)为功能函数。记无条件失效概率值为PfY, 即PfY=P{g(x)≤0}, 当基本输入变量xi取其实现值xi*时, 记条件失效概率值为PfY|xi。基本输入变量xi不确定性的消失会对失效概率造成一定的影响, 这种影响可以用PfY和PfY|xi的差异来度量[10]。当考虑xi在其整个分布域内变化时对失效概率的影响, 可以建立一个反映输入变量xi对失效概率影响程度的失效概率重要度指标。定义基本输入随机变量xi基于失效概率的矩独立重要性测度为[13]
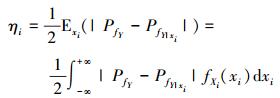
|
(1) |
式中,F表示由功能函数g(x)定义的失效域, 即F={X:g(x)≤0}, fXi(xi)为输入变量xi的概率密度函数。
(1) 式中的绝对值符号不利于运算, 所以将其等价转化为平方运算, 等价转换后的输入变量xi对失效概率的重要性测度记为δiP, 其表达式如下[8]
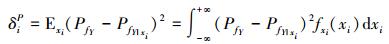
|
(2) |
而上式中的2个失效概率, 其精确表达式为输入变量的联合概率密度函数在失效域中的积分。所以无条件失效概率PfY可以改写为下式所示的失效域指示函数IF的数学期望形式
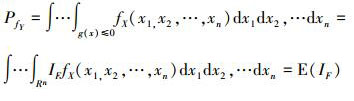
|
(3) |
式中,Rn为n维变量空间, IF为指示函数, 其定义为
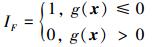
|
(4) |
类似的, 条件失效概率PfY|xi可以改写为
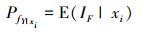
|
(5) |
将(3) 式和(5) 式带入(2) 式中, 就可以得到失效概率矩独立重要性测度与相应的失效域指示函数基于方差的重要性测度之间的关系

|
(6) |
将基于失效概率的重要性测度转化为指示函数的方差形式将会给数值模拟带来极大便利。在(6) 式的基础上, 定义一组响应量为IF的基于方差的重要度指标, 即基于失效概率的矩独立重要度指标的方差形式[11]
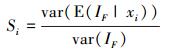
|
(7) |
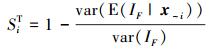
|
(8) |
式中,x~i为输入变量x中除去xi的其他分量的集合。定义Si为主效应, SiT为总效应。
由全方差公式和(3) 式得
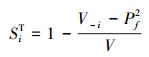
|
(10) |
在上一节中, 将(2) 式转化为方差形式, 进而可以通过一些高效的抽样方法来求解原本比较难以求解的积分问题。
传统的重要抽样法是在蒙特卡罗法的基础上引入重要抽样密度函数, 从而使得有较多的样本点落入失效域[14]。
对于(3) 式的求解, 传统的重要抽样法的公式为
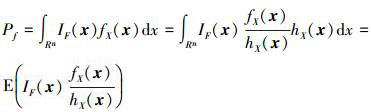
|
(11) |
式中,hX(x)为重要抽样密度函数。通常将抽样中心选择在设计点处, 以有效地增加样本点落入失效域的概率, 从而减少抽样次数, 提高计算效率。
重要抽样法虽然拥有计算效率高的优点, 但是在实际使用过程中也存在2个困难:① 随着维数的增加, 失效概率的估计值通常会与真实值相差较远, 通常是低估失效概率; ② 当设计点难以求得或者设计点数目较多时, 构造重要抽样密度函数将变得十分困难。而事实上重要抽样密度函数的好坏将直接影响计算结果精度和效率。
相比较传统的重要抽样法, 交叉熵方法(cross-entropy method)可以一定程度上避免设计点求解的困难。交叉熵的概念由Rubinstein[15]于1997年最先提出用于稀疏事件的模拟, 随后Rubinstein又将其拓展为随机优化方法[16]。
交叉熵方法实际上是一种自适应重要抽样法。与传统的重要抽样法相同, 交叉熵方法的思想也是将抽样中心移至对失效概率贡献较大的区域, 不同点在于:使用了序贯方法确定重要抽样函数, 避免了难以确定重要抽样函数的困难。
交叉熵定义为2个概率密度函数比值对数的期望

|
(12) |
从(12) 式可以看出, 当fX(x)=hX(x)时, D(f, h)=0。由此可以给求解最优重要抽样密度函数提供一个思路:设重要抽样密度为hX(x; v), 其中v为未知的分布参数, 通过选择恰当的参数v的值, 使得重要抽样密度hX(x; v)与最优重要抽样密度hX*(x)之间的差异最小, 即转化为D(h*, h)的最小化问题。
最优重要抽样密度函数的理论值为
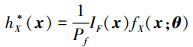
|
(13) |
式中,θ为分布参数。将(13) 式和hX(x; v)带入(11) 式, 即可将最小化问题转化为最大化问题
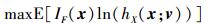
|
(14) |
对于(14) 式, 可以首先采用Monte Carlo法, 从原分布fX(x; θ)中抽取N个随机样本点{x1, x2, …, xN}则(14) 式可以转化为
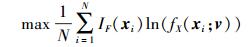
|
(15) |
对于稀疏事件, 仍然存在极少数点落入失效域的问题, 因此可以再一次进行重要抽样, 其重要抽样密度为hX(x; w), 则(14) 式可以等价为
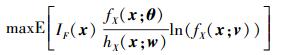
|
(16) |
定义一个权函数
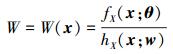
|
(17) |
从重要密度函数中抽取N个随机样本点{x1, x2, …, xN}, 可以得到
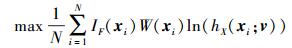
|
(18) |
可以证明(18) 式的优化问题关于v是凸的且可微, 并且对于常用的正态分布、指数分布和威布尔分布等自然指数分布族, (18) 式存在解析解, 其最优问题与下式的最小化问题等价
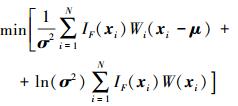
|
(19) |
可以得出最小化问题的最优解
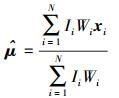
|
(20) |

|
(21) |
当失效概率非常小时, 直接应用此结论依然十分困难, 因为大部分的随机样本还是落在失效域之外。因此Rubinstein等人提出了多层交叉熵方法(multi-level cross entropy method)。这种方法是通过增加一个控制参数ρ——中间失效概率, 产生中间失效事件, 并使得中间失效事件逐渐向失效域靠近。由此构建交叉熵算法:
1) 初始化待定分布参数v0=θ, 迭代计数k=0。
2) 从hX(x; vk)产生N个随机样本{x1, x2, …, xN}, 计算功能函数值{g(xi)}, 并且对{g(xi)}从小到大排序, 得到{gi}, 求得功能函数值次序统计量的ρ分位数bk=g[ρN]。
3) 使用相同的N个随机样本{x1, x2, …, xN}, 解(19) 式,得到新的参数vk+1的估计值
4) 若bk>0, 设k=k+1, 转步骤2)。
5) 基于最终的重要抽样密度, 生成所需的随机样本。
通过引入交叉熵的概念, 改进传统的重要抽样法, 可以得到求解重要性测度的高效抽样求解法。交叉熵方法求解主效应Si和总效应SiT的步骤为[11]:
(1) 由交叉熵法求得重要抽样密度函数hX(x), 由hX(x)生成2N个样本{x1, x2, …, x2N}, 将这2N个样本分配给2组N×n的样本矩阵A和B(n为输入变量的维度), 由此得到的矩阵A和B是独立同分布的。这组样本可以通过简单随机抽样、拉丁方抽样、Sobol序列等抽样技术得到, 一般来说, Sobol序列产生的样本收敛速度优于其他方法。得到的A和B矩阵如下所示

|
(22) |
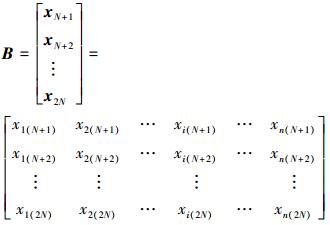
|
(23) |
(2) 求得另一组N×n的样本矩阵Ci(i=1, 2, …, n), 其中Ci的第i列来自于矩阵A, 其余的n-1列来自于矩阵B。
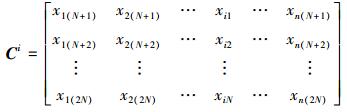
|
(24) |
(3) 对样本矩阵A、B和Ci, 计算(25) 式中的4个N维向量。
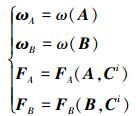
|
(25) |
式中,ω(A)和ω(B)中的元素ωA(xi)(i=1, 2, …, N)和ωB(xi)(i=N+1, …, 2N)为指示函数与权函数的乘积。
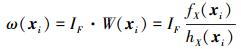
|
(26) |
函数FA是一个2n-1维的函数
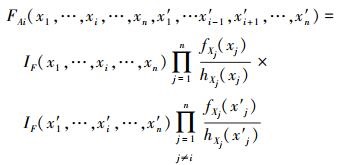
|
(27) |
函数FB是一个k+1维的函数
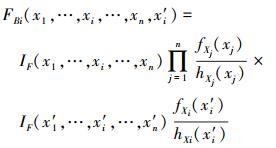
|
(28) |
由此可得4个N维向量, 即公式(25)。
(4) 主效应Si和总效应SiT的值由(29) 式和(30) 式进行计算。

|
(29) |

|
(30) |
式中

|
(31) |

|
(32) |
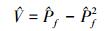
|
(33) |
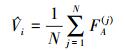
|
(34) |
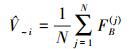
|
(35) |
式中上标j表示向量中第j个元素。
(5) Homma和Saltelli[6]还给出了计算全局重要度的误差估计方法, 结合Wei等[11]的研究, 由(36) 式和(37) 式计算估计值主效应Si和总效应SiT的概率误差。
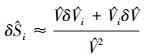
|
(36) |
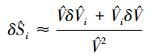
|
(37) |
式中
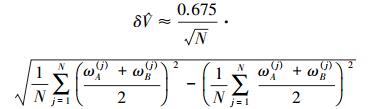
|
(38) |
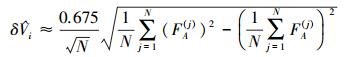
|
(39) |
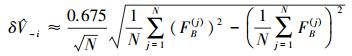
|
(40) |
为了验证本文所提方法的性能, 本节对2个数值算例和1个工程算例进行分析。分析时将蒙特卡罗法的结果作为精确解。通过对比失效概率和重要性测度的计算结果, 以及所使用的样本量来衡量方法的计算精度和效率。
算例1 考虑1个包含2个设计点的问题, 即

|
(41) |
式中,x1和x2服从标准正态分布。该问题存在2个设计点x1*={2.55, 0.50}T和x2*={-2.55, 0.50}T。
首先采用直接蒙特卡罗法在标准正态空间内求解失效概率和重要度。取样本量N=106, 可得失效概率估计值为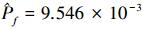
在使用重要抽样法时, 重要抽样密度需要很好地覆盖所有对失效概率贡献大的区域, 为了模拟工程中不知道设计点的情况, 假设不知道设计点2的存在。在仅知道设计点1的情况下, 构建如下的重要抽样密度
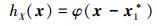
|
(42) |
样本量为N=3 000, 失效概率估计值为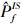
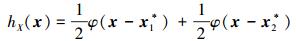
|
(43) |
在重新构建重要抽要密度之后, 失效概率估计值为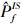
使用多层交叉熵方法求解此问题, 设定初始参数ρ=0.1, 单层样本量N0=1 000, 重要抽样样本量N=3 000。在1 000个样本中, 有498个样本点落入失效域, 迭代次数2次。这说明该方法的抽样效率非常高。得到重要抽样密度的均值和方差分别为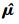
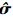
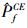
在验证了传统的重要抽样法和多层交叉熵方法计算失效概率的精度后, 采用第二节提到的方法, 使用交叉熵方法计算输入参数的重要性测度, 并与直接蒙特卡罗法和重要抽样法的结果作比较, 其结果如表 1所示。表中括号内数值表示概率误差。
| 方法 | 测度(误差) | x1 | x2 | 失效概率 | 样本量 |
| MC |  |
0.692 8(0.005 3) | 0.002 5(0.000 5) | 9.546×10-3 | 3×106 |
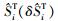 |
0.997 0(0.000 5) | 0.315 9(0.005 3) | |||
| IS 设计点未知 |
 |
0.674 0(0.024 5) | 0.005 2(0.001 5) | 4.660×10-3 | 3 000 |
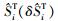 |
0.994 8(0.001 2) | 0.344 3(0.023 9) | |||
| IS 设计点已知 |
 |
0.673 6(0.027 4) | 0.002 4(0.000 8) | 9.077×10-3 | 3 000 |
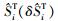 |
0.996 6(0.000 9) | 0.342 1(0.026 4) | |||
| CE |  |
0.657 7(0.049 9) | 0.002 3(0.001 8) | 9.129×10-3 | 5 000 (单层1 000) |
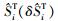 |
0.994 2(0.002 3) | 0.310 8(0.054 4) |
从表中数据可以看到一个有意思的现象, 就本算例而言, 缺失一个设计点信息导致传统重要抽样法错误地估计了失效概率, 而重要度的计算结果却是正确的。这是由于重要性测度指标中的归一化处理和极限状态函数轴对称形态引起的, 所以分布在其中一个设计点附近的样本点对其重要度的贡献与所有样本点对总体的贡献是一样的。但是这仅仅是针对这个算例的特殊情况, 并不能说明传统重要抽样法在错误计算失效概率的情况下能够得到正确的重要度。相反, 说明在全局重要性测度评估中存在陷阱。
如果是设计点已知的情况, 采用传统重要抽样法和交叉熵方法都可以得出较为精确的结果, 既有输入变量x1的重要度要大于x2。而且这2种方法相比较直接蒙特卡罗法, 所需样本量明显少, 有效地提高了计算效率。对比后2组数据, 发现交叉熵方法在确定重要抽样密度的参数时, 迭代次数为2次, 单层样本量1 000, 加上最后使用重要抽样所用的3 000个样本, 一共使用了5 000个样本。因此可以看出, 相比于已知设计点的传统重要抽样法, 交叉熵方法的计算效率略有降低。这是由于在设计点已知时, 重要抽样法的样本点可以很好地覆盖设计点, 而交叉熵方法则是通过扩大方差的方法增大样本点的覆盖范围, 以较好地覆盖所有设计点。图 1分别是设计点未知的重要抽样法、设计点已知的重要抽样法和交叉熵方法所使用的随机样本在平面上分布情况。
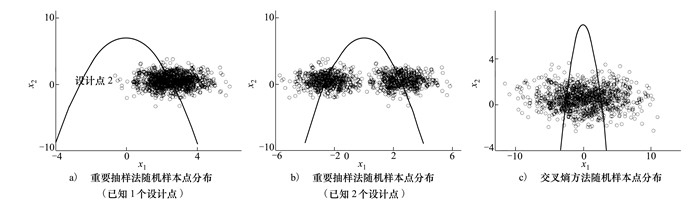
|
| 图 1 3种方法随机样本点分布情况 |
从图中可以看出, 在已知设计点的前提下, 所构造的重要抽样密度的样本很集中地分布在2个设计点的附近, 因此抽样效率极高; 而多层交叉熵方法的抽样中心位于2个设计点的中间, 由于x1的方差比较大, 所以样本点也可以比较好地覆盖2个设计点, 而相应的缺点就是计算效率和精度有所下降。不过相比较直接蒙特卡罗法, 交叉熵方法依然是大大提高了计算效率。
算例2 考虑如下的数值算例

|
(44) |
其中3个输入变量xi(i=1, 2, 3) 均服从标准正态分布。使用直接蒙特卡罗法, 重要度排序为:x3>x2>x1。将此结果作为标准值。
使用传统重要抽样法, 通过Matlab中的fminsearch函数求设计点。设计点为极限状态方程上到原点距离最小的点, 即转化为(45) 式的最小化问题
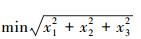
|
(45) |
式中
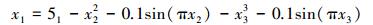
|
(46) |
即可转化为关于x2和x3的最优化问题。当x2和x3取不同的初值时, 优化结果也不尽相同。表 2给出了若干不同初值下求得的设计点以及相应的失效概率和重要度计算结果。
| 初值设计点 | 测度(误差) | x1 | x2 | x3 | 失效概率 |
| (5, 5) (0.467 2, 2.108 3, 0.165 8) |
 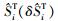 |
0.001 3(0.009 9) 0.204 2(0.000 6) |
0.139 9(0.024 7) 0.431 4(0.001 8) |
0.413 9(0.251 7) 0.750 2(0.001 1) |
7.620×10-2 |
| (-1, 1) (0.192 9, 0.094 4, 1.692 8) |
 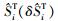 |
0.016 2(0.009 0) 0.236 6(0.042 0) |
0.104 2(0.020 9) 0.379 4(0.027 3) |
0.583 6(0.027 0) 0.906 0(0.022 7) |
7.635×10-2 |
| (-5, 5) (0.538 1, -2.103 9, 0.202 0) |
 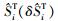 |
0.005 6(0.005 9) -0.036 5(0.222 6) |
0.137 0(0.014 7) 0.384 2(0.190 2) |
0.853 9(0.251 6) 0.763 4(0.025 5) |
6.244×10-2 |
失效概率和重要性测度的计算结果和直接蒙特卡罗法差异较大。实际上, 在增加样本量降低估计值变异系数后, 传统重要抽样法的计算结果并没有显著变好。这说明计算结果的不准确并不是样本量不足造成的, 而是因为所求得的设计点不甚理想。事实上像这种带有三角函数的极限状态函数, 由于三角函数的周期性, 设计点的计算会比较困难, 而设计点的计算误差将很大程度上影响失效概率和重要性的评估。
采用交叉熵方法, 设定初始参数ρ=0.07, 单层样本量N0=1 000, 重要抽样样本量N=5 000。其中控制参数是通过参数寻优求得。计算过程中, 多层交叉熵的迭代次数仅为1次, 总计使用6 000个样本点。抽样中心的计算结果为:均值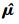
由MC法、IS法和CE法求得的3个输入变量的主效应和总效应以及相应的失效概率误差见表 3。
| 方法 | 测度(误差) | x1 | x2 | x3 | 失效概率 | 样本量 |
| MC |  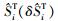 |
0.011 4(0.000 6) 0.204 2(0.000 6) |
0.197 1(0.001 0) 0.431 4(0.001 8) |
0.518 3(0.001 7) 0.750 2(0.001 1) |
8.387×10-2 | 3×106 |
| CE |  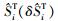 |
0.011 6(0.004 6) 0.199 0(0.028 6) |
0.201 1(0.021 7) 0.427 4(0.022 4) |
0.501 4(0.021 5) 0.763 4(0.028 4) |
8.391×10-2 | 6 000 (单层1 000) |
算例3 本算例来自文献[17], 考虑如图 2所示的工字梁问题。该问题包含8个输入变量, x=[P, L, a, S, d, bf, tw, tf]T, 各变量的分布信息如表 4所示。
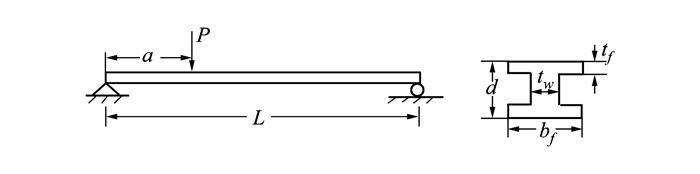
|
| 图 2 工字梁问题 |
| 变量 | 分布类型 | 均值 | 方差 |
| P | Normal | 6 070 | 200 |
| L | Normal | 120 | 6 |
| a | Normal | 72 | 6 |
| S | Normal | 170 000 | 4 760 |
| d | Normal | 2.3 | 1/24 |
| bf | Normal | 2.3 | 1/24 |
| tw | Normal | 0.16 | 1/24 |
| tf | Normal | 0.26 | 1/24 |
该问题的极限状态函数为
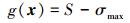
|
(47) |
式中,S为强度, σmax为最大应力, 最大应力的计算表达式为
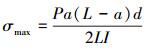
|
(48) |
式中
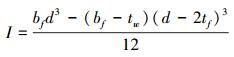
|
(49) |
使用直接蒙特卡罗法和交叉熵方法的计算结果如表 5所示。
| 方法 | 测度 | P | L | a | S | d | bf | tw | tf | 失效概率 | 样本量 |
| MC | 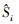 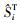 |
0.019 1 0.211 2 |
0.104 1 0.440 7 |
0.022 6 0.209 4 |
0.016 0 0.179 4 |
0.011 8 0.152 6 |
0.005 1 0.108 5 |
0.005 8 0.110 5 |
0.390 3 0.785 6 |
0.206 7 | 106 |
| CE | 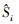 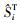 |
0.022 1 0.208 7 |
0.101 0 0.438 5 |
0.023 3 0.209 2 |
0.018 8 0.178 7 |
0.013 1 0.154 0 |
0.005 3 0.108 0 |
0.006 3 0.109 9 |
0.391 6 0.783 0 |
0.206 9 | 54 000 (单层2 000) |
根据交叉熵方法的计算结果, 输入变量重要性排序为: tf, L, a, P, S, d, tw, bf (由大到小)。这与使用蒙特卡罗法得到的结果相吻合, 也与文献中使用鞍点线抽样方法得到的结果完全一致, 证明了引入交叉熵方法计算重要性测度在工程中的可行性。值得注意的是:本算例中, 交叉熵方法相比蒙特卡罗法, 计算效率的提高并没有算例1和算例2中明显。其原因在于本算例中失效概率较大, 即使是使用直接蒙特卡罗法, 也有大约20%的样本点落入失效域。也就是说, 通过转移抽样中心来提高抽样效率的方法, 在小失效概率事件中会有更为显著的优势。
4 结论本文针对失效概率的重要性测度分析, 提出了一种基于交叉熵方法的高效评估方法。与传统重要抽样方法相比, 避免了设计点位置和个数的求解。所提方法通过自适应移动抽样中心的方法, 逐步确定一个合理的重要抽样函数, 回避多设计点问题, 使得更多的样本点落入失效域, 以提高在失效概率和重要性测度的计算效率。相比于传统的重要抽样法, 交叉熵方法可能略微降低了计算效率, 但是免去了设计点求解的困难, 适用于非线性极限状态函数和多设计点的复杂情况, 为重要性测度研究提供了一个新的思路和方向。文中算例不但验证了该方法的优越性, 同时也提供了传统重要抽样法明显不足的典型例证。
| [1] |
吕震宙, 李璐祎, 宋述芳, 等. 不确定性结构系统的重要性分析理论与求解方法[M]. 北京: 科学出版社, 2015.
Lü Zhengzhou, Li Luyi, Song Shufang, et al. Importance Analysis Theory and Solution Method for Uncertain Structural Systems[M]. Beijing: Science Press, 2015. (in Chinese) |
| [2] | Saltelli A. Sensitivity Analysis for Importance Assessment[J]. Risk Analysis, 2002, 22(3): 579-590. DOI:10.1111/risk.2002.22.issue-3 |
| [3] | Iman R L, Hora S C. A Robust Measure of Uncertainty Importance for Use in Fault Tree System Analysis[J]. Risk Analysis, 1990, 10(3): 401-406. DOI:10.1111/risk.1990.10.issue-3 |
| [4] | Sobol I M. Sensitivity Estimates for Nonlinear Mathematical Models[J]. Matem Mod, 1993, 2(1): 112-118. |
| [5] | Saltelli A, Scott M. The Role of Sensitivity Analysis in the Corroboration of Models and Itslink to Model Structural and Parametric Uncertainty[J]. Reliability Engineering & System Safety, 1997, 57(1): 1-4. |
| [6] | Homma T, Saltelli A. Importance Measures in Global Sensitivity Analysis of Nonlinear Models[J]. Reliability Engineering & System Safety, 1996, 52(1): 1-17. |
| [7] | Saltelli A. Making Best Use of Model Evaluations to Compute Sensitivity Indices[J]. Computer Physics Communications, 2002, 145(2): 280-297. DOI:10.1016/S0010-4655(02)00280-1 |
| [8] | Li L, Lü Z, Feng J, et al. Moment-Independent Importance Measure of Basic Variable and Its State Dependent Parameter Solution[J]. Structural Safety, 2012, 38: 40-47. DOI:10.1016/j.strusafe.2012.04.001 |
| [9] |
张磊刚, 吕震宙, 陈军. 基于失效概率的矩独立重要性测度的高效算法[J]. 航空学报, 2014, 35(08): 2199-2206.
Zhang Leigang, Lü Zhengzhou, Chen Jun. An Efficient Method for Failure Probability-Based Moment-Independent Importance Measure[J]. Acta aeronautica et Astronautica Sinica, 2014, 35(8): 2199-2206. (in Chinese) |
| [10] |
李贵杰, 吕震宙, 宋述芳. 基本变量对失效概率重要性测度分析的新方法[J]. 力学与实践, 2010, 32(2): 71-75.
Li Guijie, Lü Zhengzhou, Song Shufang. A New Method for Analyzing Importance Measure of Basic Variable Effect on Failure Probability[J]. Mechanics in Engineering, 2010, 32(2): 71-75. (in Chinese) |
| [11] | Wei P, Lu Z, Hao W, et al. Efficient Sampling Methods for Global Reliability Sensitivity Analysis[J]. Computer Physics Communications, 2012, 183(8): 1728-1743. DOI:10.1016/j.cpc.2012.03.014 |
| [12] | Cheng L, Lu Z, Zhang L. Application of Rejection Sampling Based Methodology to Variance Based Parametric Sensitivity Analysis[J]. Reliability Engineering & System Safety, 2015, 142: 9-18. |
| [13] | Cui L, Lü Z, Zhao X. Moment-Independent Importance Measure of Basic Random Variable and Its Probability Density Evolution Solution[J]. Science China Technological Sciences, 2010, 53(4): 1138-1145. DOI:10.1007/s11431-009-0386-8 |
| [14] |
吴斌, 欧进萍. 结构动力可靠度的重要抽样法[J]. 计算力学学报, 2001, 18(4): 478-482.
Wu Bin, Ou Jinping. Importance Sampling Techniques in Dynamical Structural Reliability[J]. Chinese Journal of Computational Mechanics, 2001, 18(4): 478-482. (in Chinese) |
| [15] | Rubinstein R Y. Optimization of Computer Simulation Models with Rare Events[J]. European Journal of Operational Research, 1997, 99(1): 89-112. DOI:10.1016/S0377-2217(96)00385-2 |
| [16] | Rubinstein R. The Cross-Entropy Method for Combinatorial and Continuous Optimization[J]. Methodology & Computing in Applied Probability, 1999, 1(2): 127-190. |
| [17] | Huang B, Du X, Huang B, et al. Uncertainty Analysis by Dimension Reduction Integration and Saddlepoint Approximations[J]. Journal of Mechanical Design, 2006, 128(1): 1143-1152. |


