Volterra级数[1]作为一种描述非线性时不变系统的数学模型, 对于任意有限记忆时间系统总能由Volterra级数以任意阶精度逼近[2], 目前已经在许多领域得到了应用, 如气动弹性[3]、电子工程[4]、机械工程[5]等。
Volterra级数应用于非线性系统建模的关键在于Volterra核的辨识, 核辨识面临的主要困难是大量的待辨识参数。由于表示核的参数数量随核阶次的增加而呈指数增加, 高阶核的引入将带来大量的待辨识参数。针对这一问题, 许多研究者提出了解决方法。一类是对高阶核进行截断以减少待辨识参数, 如Balajewicz等[6]保留前四阶核的主对角分量舍去其他部分实现了NACA0012翼型在高亚声速区小迎角下运动时俯仰力矩系数建模, Safari等[7]研究了保留主对角线附近分量时射频功率放大器的二阶核辨识。这类方法由于略去了不同时刻的输入相互作用对系统产生的非线性影响, 降低了Volterra级数对非线性系统的表示能力。另外一大类方法是基函数法, 即用一组基函数表示Volterra核, 将问题转化为少数展开系数的估计问题。例如, Moodi等[8]用Laguerre基函数表示Volterra核, 王云海等[9]以Chebyshev函数为基进行了翼型在跨声速区小迎角下沉浮运动时的升力系数建模。基函数的类型和性质对辨识结果存在很大影响, 相较于这些全局支撑的基函数, 小波基具有局部支撑、正交、对称或反对称等更多优良性质, 可以更精准地反映对象的细节特征。相关研究例如Maheswaran等[10]利用二阶Daubechies小波实现了多输入、单输出非线性系统的Volterra核辨识。
本文采用Prazenica等[11]提出的分段二次多小波(piecewise quadratic multiwavelet, PQMW)为基函数, 其相比普通单小波的优点在于同时具有紧支性、正交性、对称或反对称性, 而且满足分段光滑, 更适合于表示连续系统的光滑Volterra核。通过辨识典型的非线性振荡器的前两阶Volterra核验证了分段二次多小波应用于Volterra核辨识的有效性, 同时验证结果表明由前两阶核就能准确计算该系统在不同输入下的响应。在高阶核辨识中, 输入信号能否激发系统中不同频率相互作用产生的非线性影响是直接决定Volterra高阶核辨识精度的重要因素。为此, 本文在扫频信号的基础上设计了一种适合于二阶核辨识的输入称为二维扫频, 试验结果表明其对二阶核的辨识效果明显优于扫频输入。
1 Volterra核辨识1.1 Volterra级数基本理论Volterra级数理论[1]指出, 对于非线性时不变单输入单输出系统, 输入输出之间的关系可由如下多维卷积的无穷和表示:
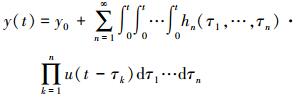
|
(1) |
式中:u(t)是系统输入, y(t)是对应的输出, y0是定常状态的响应值, hn(τ1, τ2, …, τn)是n阶Volterra核, 也是线性系统的一维单位脉冲响应在高维空间的推广。若已知各阶核, 系统对于输入的响应可由(1) 式计算得到。不失一般性, 通常假定高阶核hn(n≥2) 满足对称性, 即hn(τ1, τ2, …, τn)=hn(τπ(1), τπ(2), …, τπ(n)), 其中π(1), π(2), …, π(n)是1, 2, …, n的所有排列[1]。
对于线性系统, Volterra级数的高阶核hn均为零, 仅一阶核h1就能完全描述系统[12], 即
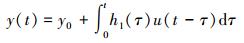
|
(2) |
对于非线性系统, 一阶核代表了系统的线性部分, 高阶核代表了系统的非线性影响。尽管Volterra级数是无穷项的和, 但对于真实物理系统, 其非线性影响随核阶次的增加迅速衰减, 因此一般前几项就能很好的近似表示系统[2]。本文仅考虑一阶核和二阶核, 此时(1) 式简化为
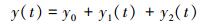
|
(3) |
式中
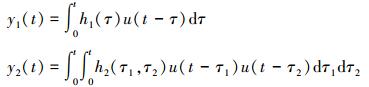
|
(4) |
y1(t)、y2(t)分别为一阶核和二阶核产生的响应。
Prazenica等[11]通过直接求解(3) 式同时辨识各阶核, 由于各阶核的响应之间存在相互影响将导致辨识精度降低。为了避免这种情况可将各阶核的响应分离然后分别辨识一阶核和二阶核。对系统施加不同幅值的激励, 在定常响应为零的情况下得
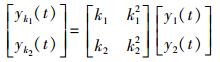
|
(5) |
式中,yk1(t)、yk2(t)分别为不同幅值k1、k2的输入产生的输出, 求解(5) 式得一阶核的响应y1(t)和二阶核的响应y2(t), 然后根据(4) 式可分别辨识一阶核和二阶核。
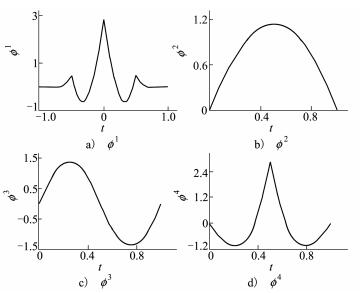
1.2 分段二次多小波分段二次多小波是Prazenica等[11]设计的一种满足分段二次多项式的多小波, 其尺度函数曲线如图 1所示。
|
| 图 1 分段二次多小波的尺度函数 |
分段二次多小波同时具有紧支性、正交性、对称或反对称性等优良性质, 而且分段二次多项式满足分段光滑, 因此非常适合于表示Volterra核[11]。尺度函数的伸缩和平移形式
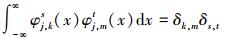
|
(6) |
式中整数j称为伸缩因子决定了函数的分辨率, 整数k称为平移因子决定了函数的作用位置, δk, m, δs, t均满足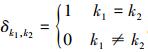
Volterra级数的一阶核响应
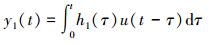
|
(7) |
将(7) 式离散, 输入采用零阶保持, 采样频率为2j Hz, 总的数据点为N, 输入的离散形式为[11]
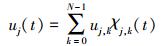
|
(8) |
式中

|
(9) |
一阶核在伸缩因子j1下以一组个数为r的基函数φ展开, 表示形式为[11]
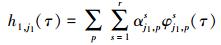
|
(10) |
将(8) 式和(10) 式代入(7) 式, 得一阶核响应的离散表示式
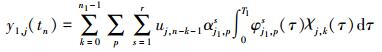
|
(11) |
式中:n=1, 2, …, N, tn=2-jn, n1=min(n, 2jT1), T1为一阶核的持续时间, 即经过时间T1后一阶核近似衰减到零。
将(11) 式写为矩阵形式[11]
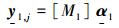
|
(12) |
式中, 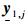
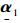
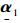
Volterra级数的二阶核响应
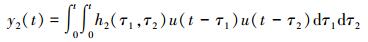
|
(13) |
与一阶核类似将(13) 式离散, 二阶核在伸缩因子j2下以一组个数为r的基函数φ的张量积展开, 表示形式为[11]
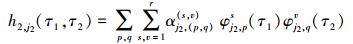
|
(14) |
将(8) 式和(14) 式代入(13) 式, 得二阶核响应的离散表示式

|
(15) |
式中:n=1, 2, …, N, n2=min(n, 2jT2), T2为二阶核的持续时间。
将(15) 式写为矩阵形式[11]
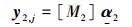
|
(16) |
式中, 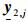
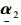
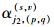
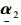
输入的选择和设计在系统辨识中至关重要, 直接决定了系统参数的辨识精度。Volterra核的辨识中, 一阶核辨识属于线性系统辨识问题, 有多种输入如脉冲、扫频可以采用, 高阶核辨识属于非线性系统辨识问题, 目前缺乏通用的输入信号。本文提出了一种适合于二阶核辨识的二维扫频输入。
从频域角度分析高阶核辨识中对输入的要求, n阶Volterra核的傅里叶变换Hn(ω1, ω2, …, ωn)称为n阶广义频率响应函数(generalized frequency response function, GFRF)。一阶GFRFH1(ω)以单一频率ω为自变量, 线性系统辨识中的输入如扫频信号通过提供系统在不同频率的响应反映出了H1(ω)中ω取不同值时的系统特性, 因而能实现一阶核的辨识。二阶GFRFH2(ω1, ω2)以ω1、ω2为自变量, 此时扫频等信号仍然只能反映单一频率下的系统特性即H2(ω, ω), 无法反映2个不同频率共同作用对系统的影响, 因而难以实现二阶核的准确辨识, 更高阶核可类似分析。针对这一问题, 本文设计了一种适合于二阶核辨识的输入称为二维扫频, 其为两部分的叠加, 第一部分为简单的扫频信号, 代表ω1连续变化, 第二部分为多个扫频的重复, 代表ω2不断在频率范围内重复变化, 同时相位相差π/2。两部分耦合, 在极限情况下, 第二部分重复时间趋于零即重复次数趋于无穷大时, ω1在不同频率下ω2都从初始频率变化到终止频率, 即实现了两两不同频率的共同作用。二维扫频(two dimensional chirp, Chirp2D)具体表示式如下
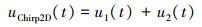
|
(17) |
式中
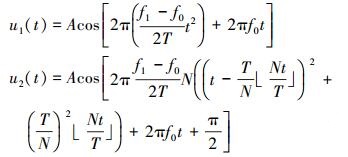
|
(18) |
式中,f0和f1分别是扫频的初始频率和终止频率, T是扫频时间, A是输入幅值, ⌊⌋是向下取整, N是重复扫频的次数, 每一次重复都是频率f0到f1的线性扫频。T取50 s, f0=0 Hz, f1=2 Hz, N=3时的二维扫频输入如图 2所示。
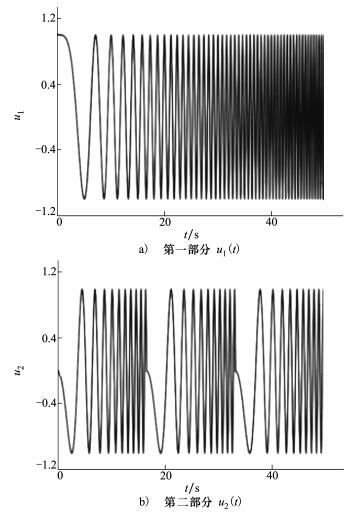
|
| 图 2 二维扫频输出 |
为了与二维扫频比较, 这里简单介绍常用的扫频信号。扫频输入在线性系统辨识中广泛使用, 常用的包括线性扫频和指数扫频, 表示式如下[13]
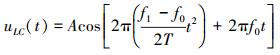
|
(19) |
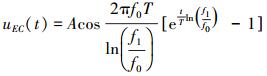
|
(20) |
式中,LC表示Linear Chirp即线性扫频, EC表示Exponential Chirp即指数扫频, 不失一般性这里假定初始相位为零。2种扫频的频率变化分别为
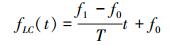
|
(21) |
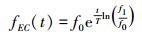
|
(22) |
可见线性扫频的频率呈线性变化, 而指数扫频的频率则呈指数变化, 都从初始时刻的f0变化到结束时刻的f1。
3 算例3.1 基函数验证振荡器Oscillator在机械结构中广泛出现, 具有二次非线性的Oscillator方程[14]表示如下
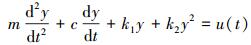
|
(23) |
式中, m是质量, c是阻尼系数, k1是线性刚度系数, k2是二次刚度系数, k2y2是该系统的非线性项。各项参数为m=1 kg, c=3 N·s/m, k1=4π2 N/m, k2=4π2 N/m2。
系统辨识所用的输入为第2节中的二维扫频, 频率范围为0~7 Hz, 幅值A=1, 重复扫频次数N=10, 持续时间为50 s, 采样频率为1 024 Hz(j=10), 2次试验的输入幅值分别为1、0.5。
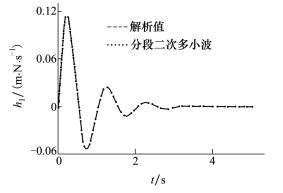
采用分段二次多小波辨识该系统的一阶核和二阶核。对于一阶核, 持续时间为T1=5 s, 伸缩因子取j1=2。辨识结果与解析结果的比较如图 3所示。
|
| 图 3 Oscillator的一阶Volterra核 |
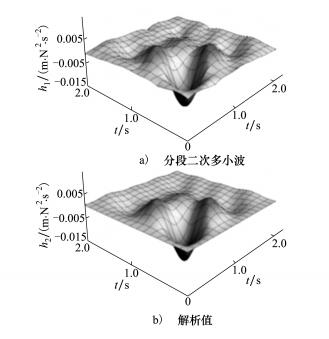
对于二阶核, 持续时间为T2=2 s, 取j2=1, 辨识结果与解析结果的比较如图 4所示。已知系统方程推导各阶Volterra核解析式的方法见文献[15], 一阶核和二阶核在拉普拉斯域的表示式如下
|
| 图 4 Oscillator的二阶Volterra核 |

|
(24) |
对(24) 式进行拉普拉斯反变换即可得一阶核和二阶核在时域的解析表示式。
由图 3和图 4可见, 以分段二次多小波为基函数辨识得到的Oscillator系统的一阶核和二阶核与解析值非常接近, 表明了该基函数的有效性。
下面验证Volterra级数表示系统的能力, 输入分别取
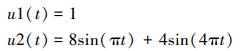
|
(25) |
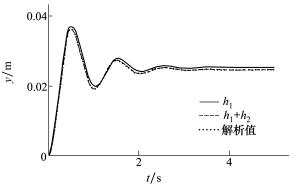
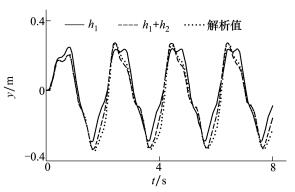
由一阶核、二阶核计算的系统响应与直接求解方程得到的解如图 5和图 6所示, 可见在单位阶跃响应中, 一阶核计算的结果已经比较接近真实解, 考虑二阶核后计算的响应与真实解非常吻合。在第二种输入下, 由一阶核计算的响应与真实解存在较大误差, 采用二阶核后计算的响应有明显改进, 表明Volterra级数能准确表示该非线性系统。
|
| 图 5 Oscillator在输入u1(t)下的响应 |
|
| 图 6 Oscillator在输入u2(t)下的响应 |
下面以Oscillator为例, 比较在第2节中的3种输入下一阶核和二阶核的辨识结果。3种输入的激励时间均为50 s, 频率变化范围均为0~7 Hz, 幅值均为A=1。
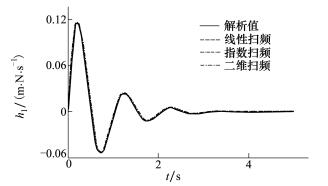
采用3种输入辨识得到的一阶核如图 7所示, 可见对于一阶核的辨识, 也即系统单位脉冲响应的辨识, 3种输入都能很好地激励系统。
|
| 图 7 不同输入辨识的Oscillator的一阶Volterra核 |
为了比较二阶核的辨识精度, 定义二阶核的相对均方根误差(relative root means square error, RRMSE)如下
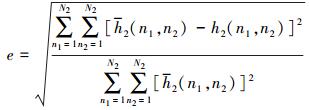
|
(26) |
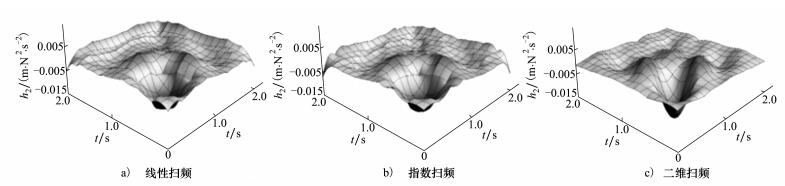
式中,h2(n1, n2)和h2(n1, n2)分别是二阶核的解析结果和辨识结果, N2是二阶核的数据点数。二阶核的辨识结果如图 8所示, 误差见表 1。可见线性扫频和指数扫频均存在很大误差, 而二维扫频得到了相当准确的结果, 表明对于二阶核的辨识二维扫频要优于其他2种输入。
|
| 图 8 不同输入辨识的Oscillator的二阶Volterra核 |
本文研究了采用Volterra级数对非线性时不变系统进行建模时Volterra核的辨识问题。为了减少待辨识参数, 以分段二次多小波为基函数将Volterra核展开, 实现了一阶核和二阶核的辨识。通过非线性振荡器进行算例验证, 结果表明分段二次多小波能很好的用于一阶核和二阶核的辨识, 而且由Volterra级数能准确计算系统在不同输入下的响应。同时本文提出了一种能反映系统中不同频率相互作用产生的非线性影响的输入信号, 试验结果表明本文提出的二维扫频输入相较于线性扫频和指数扫频更适合于二阶核的辨识, 可作为不同领域中非线性系统Volterra核辨识时输入设计的一种重要选择。
| [1] | Schetzen M. The Volterra and Wiener Theories of Nonlinear Systems[M]. Malabar, Florida: Krieger Pub, 2006. |
| [2] | Boyd S, Chua L O. Fading Memory and the Problem of Approximating Nonlinear Operators with Volterra Series[J]. IEEE Trans on Circuits and Systems, 1985, 32(11): 1150-1161. DOI:10.1109/TCS.1985.1085649 |
| [3] | Prazenica R J, Reisenthel P H, Kurdila A J, et al. Volterra Kernel Extrapolation for Modeling Nonlinear Aeroelastic Systems at Novel Flight Conditions[J]. Journal of Aircraft, 2007, 44(1): 149-162. DOI:10.2514/1.22764 |
| [4] | Zhu A, Pedro J C, Brazil T J. Dynamic Deviation Reduction-Based Volterra Behavioral Modeling of RF Power Amplifiers[J]. IEEE Trans on Microwave Theory and Techniques, 2006, 54(12): 4323-4332. DOI:10.1109/TMTT.2006.883243 |
| [5] | Omran A, Newman B. Nonlinear Analytical Multi-Dimensional Convolution Solution of the Second Order System[J]. Nonlinear Dynamics, 2010, 62(4): 799-819. DOI:10.1007/s11071-010-9764-9 |
| [6] | Balajewicz M, Dowell E. Reduced-Order Modeling of Flutter and Limit-Cycle Oscillations Using the Sparse Volterra Series[J]. Journal of Aircraft, 2012, 49(6): 1803-1812. DOI:10.2514/1.C031637 |
| [7] | Safari N, Roste T, Fedorenko P, et al. An Approximation of Volterra Series Using Delay Envelopes, Applied to Digital Predistortion of RF Power Amplifiers with Memory Effects[J]. IEEE Microwave and Wireless Components Letters, 2008, 18(2): 115-117. DOI:10.1109/LMWC.2007.915099 |
| [8] | Moodi H, Bustan D. On Identification of Nonlinear Systems Using Volterra Kernels Expansion on Laguerre and Wavelet Function[C]//Control and Decision Conference(CCDC), 2010:1141-1145 |
| [9] |
王云海, 韩景龙, 张兵, 等. 空气动力二阶核函数辨识方法[J]. 航空学报, 2014, 35(11): 2949-2957.
Wang Yunhai, Han Jinglong, Zhang Bing, et al. Identification Method of Second-Order Kernels in Aerodynamics[J]. Acta Aeronautica et Astronautica Sinca, 2014, 35(11): 2949-2957. (in Chinese) |
| [10] | Maheswaran R, Khosa R. Wavelet Volterra Coupled Models for Forecasting of Nonlinear and Non-Stationary Time Series[J]. Neurocomputing, 2015, 149(Part B): 1074-1084. |
| [11] | Prazenica R J, Kurdila A J. Multiwavelet Constructions and Volterra Kernel Identification[J]. Nonlinear Dynamics, 2006, 43(3): 277-310. DOI:10.1007/s11071-006-8323-x |
| [12] | Silva W A. Application of Nonlinear Systems Theory to Transonic Unsteady Aerodynamic Responses[J]. Journal of Aircraft, 1993, 30(5): 660-668. DOI:10.2514/3.46395 |
| [13] | Tronchin L. The Emulation of Nonlinear Time-Invariant Audio Systems with Memory by Means of Volterra Series[J]. Journal of the Audio Engineering Society, 2012, 60(12): 984-996. |
| [14] | Cheng C M, Peng Z K, Zhang W M, et al. Wavelet Basis Expansion-Based Volterra Kernel Function Identification through Multilevel Excitations[J]. Nonlinear Dynamics, 2014, 76(2): 985-999. DOI:10.1007/s11071-013-1182-3 |
| [15] | Marzocca P, Librescu L, Silva W A. Aeroelastic Response of Nonlinear Wing Sections Using a Functional Series Technique[J]. AIAA Journal, 2002, 40(5): 813-824. DOI:10.2514/2.1735 |


