2. 西北工业大学 力学与土木建筑学院, 陕西 西安 710072
b族方程作为一类重要的浅水波方程,涵盖了浅水波传播问题中的许多重要物理性质[1-2]。Camassa和Holm推导了一个完全可积的、具有bi-Hamiltonian结构的b族方程 (b=2情形) 及其无穷守恒律,并采用渐近展开方法得到了其尖波解。为了表彰Camassa和Holm在b族方程可积性质及其守恒性质方面的重要贡献,学术界将b=2的情形对应的方程命名为Camassa-Holm方程[1]。Degasperis和Procesi进一步研究了另一个具有bi-Hamiltonian结构且完全可积的b族方程 (b=3情形) 的尖波解的存在性,并将b=3的情形对应的方程命名为Degasperis-Procesi方程[2]。
自从Camassa-Holm方程和Degasperis-Procesi方程创立以来,其尖波解传播的相关定性性质研究引起了学术界的极大兴趣。采用的研究方法中,多辛分析方法非常值得关注。多辛分析方法是Bridges教授基于多辛几何概念提出的[3],其基本思想是在无限维动力学系统数值模拟过程中,通过关注系统多辛结构的保持情况,考察数值方法在保持系统局部几何性质方面的性能[3-5]。这一思想是对我国冯康院士创立的辛几何算法[6]思想的延伸和推广,尖波解正是反映系统局部几何性质的典型结果。为此,Cohen等人[7]、朱华军教授等人[8]和张宇博士等[9]分别构造了不同的多辛格式模拟Camassa-Holm方程尖波解的传播过程。鉴于Degasperis-Procesi方程不具有严格多辛形式这一难点问题,胡伟鹏教授等人通过构造b族方程统一对称形式,研究了quasi-Degasperis-Procesi方程尖波解的传播过程及其传播过程中多种守恒律的保持情况[10]。本文将在b族方程统一对称形式基础上,采用多辛分析方法研究b=0这种特殊情形下尖波解的传播问题,为b族方程尖波解性质研究提供参考。
1 b族方程对称性的回顾文献[10]中,针对b族方程:
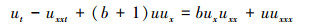
|
(1) |
构造了统一的对称形式, 即多辛形式。在b≠3且b≠4的情形下, 方程 (1) 可以写成如下对称形式:
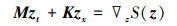
|
(2) |
式中:z=[u, ϕ, w, ψ, v]T∈R5为状态向量, 其各分量之间的相互关系由下式定义

|
(3) |
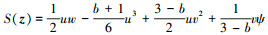
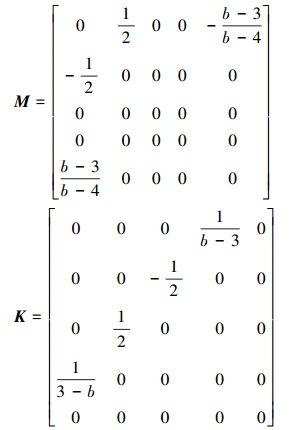
|
本文考虑b=0的情形, 则以上对称形式具体可以表述为
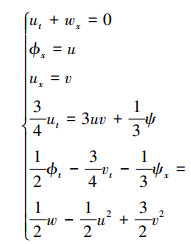
|
(4) |
其多辛结构为
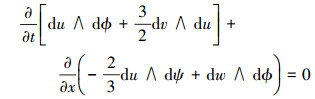
|
(5) |
依据多辛理论, 多辛算法能够很好保持系统局部几何性质的本质原因是多辛差分格式在每一网格点上都能很好地满足多辛结构。因此, 离散多辛结构的满足情况将在本文中作为检验算法性能的重要指标。
2 多辛Box格式及其等价形式数值方法的计算效率与计算量之间存在天然的竞争关系, 多辛分析方法也不能例外。本文只是拟采用多辛方法探索b族方程在b=0情形下尖波解的传播特性, 因此采用Box方法这种构造多辛离散格式最简单的离散方法来离散多辛形式, 更能体现出多辛方法的诸多优点。方程组 (4) 的多辛Box离散格式为
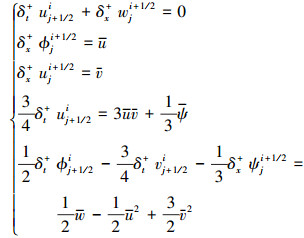
|
(6) |
多辛Box离散格 (6) 式满足离散的多辛守恒律
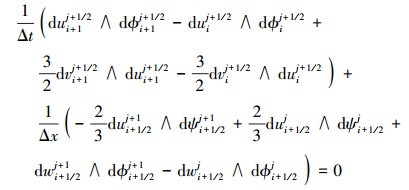
|
(7) |
离散的局部能量守恒律和离散的局部动量守恒律在文献[10]中已经给出了详细的数学证明, 在此不再赘述。为了进一步减小计算量, 将网格中点值平均到整数网格点上, 并通过层间代数运算, 削去格式 (6) 中的中间变量ϕ, w, ψ, v, 得到等价于多辛Box离散格 (6) 式的新多辛隐式格式

|
(8) |
式中:Δt和Δx分别为时间步长和空间步长, δt、δt2分别为时间方向的一阶和二阶差分算子, δx、δx2和δx3分别为空间方向的一阶、二阶和三阶差分算子, u= 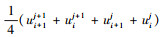
由于格式 (8) 是由Box格式 (6) 等价推导得到的, 而Box格式已经被证明是稳定性和收敛性较好的多辛格式[5, 11]。因此, 其在数值特性方面, 包括稳定性、收敛性和保结构性质, 都能够得到很好地保证。但是, 从计算过程中所需的变量存储容量看, 相对于Box格式 (6)、格式 (8) 所需的变量存储要少得多, 这也是已有报道中许多研究者采用等价格式, 而不采用原始的Box格式进行数值模拟的原因[12]。
3 尖波解传播特性研究已有研究表明, Camassa-Holm方程和Degasperis-Procesi方程均存在稳定传播的尖波解[1, 2, 13-15], 针对本文研究对象, 当b族方程中缺少uxuxx项时 (即b=0), 该系统是否存在稳定传播的尖波解呢?
考虑使得Camassa-Holm方程和Degasperis-Procesi方程形成稳定传播的尖波解的初值条件:

|
(9) |
取步长Δt=0.01, Δt=0.02, 定义求解域为x∈[-5,5], 模拟尖波解的传播过程。在模拟过程中, 依据下式记录每一网格点处多辛守恒律残差:
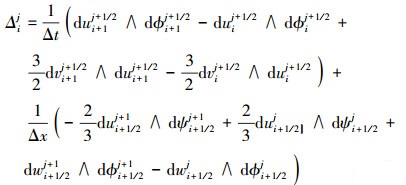
|
(10) |
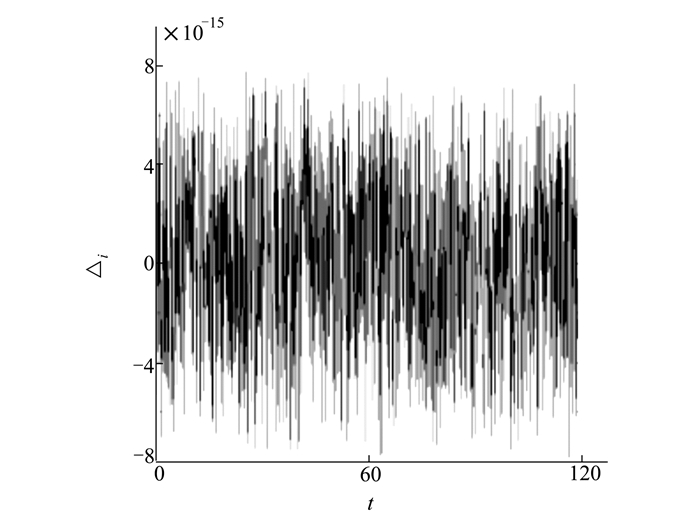
然后对Δij在x方向采用梯形积分格式进行数值积分, 得到每一时刻多辛守恒律残差Δi, 结果如图 1所示。从图 1中可以看出:在长时间数值模拟过程中 (t∈[0,120]), 多辛守恒律残差一直在[-8×10-15, 8×10-15]区间震荡。这一结果充分说明了本文所构造的与Box格式等价的差分格式 (8) 具有较好的长时间数值稳定性和保结构性能。因此, 采用这一数值格式模拟尖波解传播过程的数值结果应该能够较为准确地反映尖波解传播过程中的局部几何性质。
|
| 图 1 模拟过程中的多辛守恒律残差 |
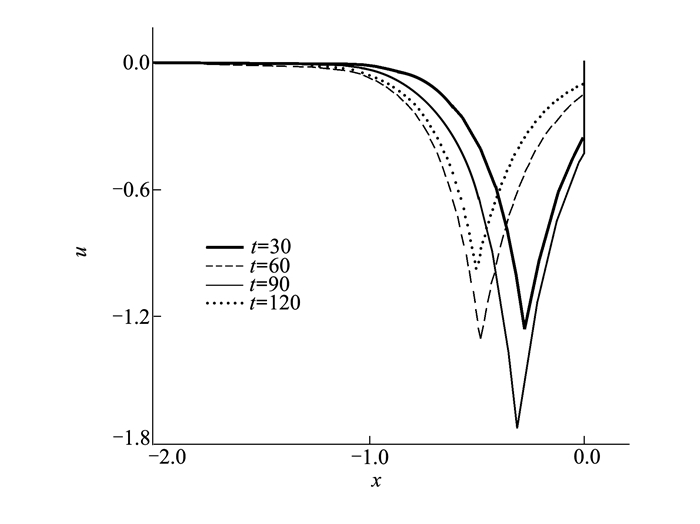
图 2给出了不同时刻尖波解的波形图 (由于波形图具有对称性, 此处我们只给出了在x∈[-2, 0]区间的波形图), 从波形图能够明显看出:由于缺少uxuxx项, 尖波解在传播过程中, 并不能始终保持两列尖波碰撞过程发生在x=0的截面上, 同时, 随着时间的流逝, 尖波的幅值有减小趋势, 而尖波宽度随着时间流逝有总体增大的趋势 (波形图中t=90不遵循这一规律)。以上结果和现象说明, 当b=0时, b族方程不存在稳定传播的尖波解。
|
| 图 2 不同时刻尖波解的波形图 |
本文基于已有关于b族方程bi-Hamiltonian结构及其统一的对称形式方面的研究成果,针对b=0这一特殊情形,发展了多辛算法,用于探索这一特殊情形下,b族方程是否存在稳定传播的尖波解。
将b=0代入b族方程统一的对称形式,得到了这一特殊情形下b族方程的多辛形式和多辛结构 (即多辛守恒律),随后构造了一种等价于Box多辛格式的隐式多辛离散格式。在适当的初值条件下,利用构造的隐式多辛格式模拟尖波解传播过程,多辛守恒律残差数值结果表明:本文构造的多辛格式具有良好的长时间数值稳定性和保结构数值性能。从尖波解传播过程的波形图看,b=0这一特殊情形下,b族方程并不存在稳定传播的尖波解。这一研究结果为b族方程尖波解的存在性数值研究提供了新的途径。
| [1] | Camassa R, Holm D D. An Integrable Shallow-Water Equation with Peaked Solitons[J]. Physical Review Letters, 1993, 71(11): 1661–1664. DOI:10.1103/PhysRevLett.71.1661 |
| [2] | Degasperis A, Procesi M, Asymptotic Integrability.//Degasperis A, Gaeta G. Symmetry and Perturbation Theory[M]. Singapore, World Scientific, 1999:23-37 |
| [3] | Bridges T J. Multi-Symplectic Structures and Wave Propagation[J]. Mathematical Proceedings of The Cambridge Philosophical Society, 1997, 121(1): 147–190. DOI:10.1017/S0305004196001429 |
| [4] | Bridges T J. A Geometric Formulation of the Conservation of Wave Action and Its Implications for Signature and the Classification of Instabilities[J]. Proceeding of the Royal Society, 1997, 456: 1365–1395. |
| [5] | Bridges T J, Reich S. Multi-Symplectic Integrators:Numerical Schemes for Hamiltonian PDEs That Conserve Symplecticity[J]. Physics Letters A, 2001, 284(4/5): 184–193. |
| [6] | Feng K. On Difference Schemes and Symplectic Geometry[C]//Proceedings of the 5th International Symposium on Differential Geometry & Differential Equations, 1985:42-58 |
| [7] | Cohen D, Owren B, Raynaud X. Multi-Symplectic Integration of the Camassa-Holm Equation[J]. Journal of Computational Physics, 2008, 227(11): 5492–5512. DOI:10.1016/j.jcp.2008.01.051 |
| [8] | Zhu H J, Song S H, Tang Y F. Multi-Symplectic Wavelet Collocation Method for the Nonlinear Schrödinger Equation and the Camassa-Holm Equation[J]. Computer Physics Communications, 2011, 182(3): 616–627. DOI:10.1016/j.cpc.2010.11.003 |
| [9] | Zhang Y, Deng Z C, Hu W P. Multisymplectic Method for the Camassa-Holm Equation[J]. Advances in Difference Equations, 2016, 7: 1–2. |
| [10] | Hu W P, Deng Z C, Zhang Y. Multi-Symplectic Method for Peakon-Antipeakon Collision of Quasi-Degasperis-Procesi Equation[J]. Computer Physics Communications, 2014, 185(7): 2020–2028. DOI:10.1016/j.cpc.2014.04.006 |
| [11] | Bridges T J, Reich S. Multi-Symplectic Spectral Discretizations for the Zakharov-Kuznetsov and Shallow Water Equations[J]. Physica D, 2001, 152: 491–504. |
| [12] | Hu W P, Deng Z C. Multi-Symplectic Method for Generalized Boussinesq Equation[J]. Applied Mathematics and Mechanics (English Edition), 2008, 29(7): 927–932. DOI:10.1007/s10483-008-0711-3 |
| [13] | Degasperis A, Holm D D, Hone A N W. A New Integrable Equation with Peakon Solutions[J]. Theoretical And Mathematical Physics, 2002, 133(2): 1463–1474. DOI:10.1023/A:1021186408422 |
| [14] | Kolev B. Some Geometric Investigations on the Degasperis-Procesi Shallow Water Equation[J]. Wave Motion, 2009, 46(6): 412–419. DOI:10.1016/j.wavemoti.2009.06.005 |
| [15] | Yu C H, Sheu T W H. A Dispersively Accurate Compact Finite Difference Method for the Degasperis-Procesi Equation[J]. Journal of Computational Physics, 2013, 236: 493–512. DOI:10.1016/j.jcp.2012.10.046 |
2. School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi'an 710072, China


