2. 西安邮电大学 电子工程学院, 陕西 西安 710121
近年来已有一些文献研究了竞争失效产品加速寿命试验的统计分析与优化设计。文献[1]研究了广义指数分布竞争失效产品步进应力加速(步加)寿命试验的统计分析,给出了分布参数的点估计和置信区间。文献[2]在失效原因服从对数正态分布的情形下,利用EM算法研究了竞争失效产品加速寿命试验的极大似然分析。文献[3]基于Copula函数建立了恒定应力加速(恒加)寿命试验中相依竞争失效模型,给出了二维和多维失效模式下指数分布参数的极大似然估计和最小方差估计。文献[4]在竞争失效原因相依的情形下应用Copula函数连接了边缘分布和联合分布函数,给出了未知参数的极大似然估计,并简单介绍了正确建立Copula连接函数的方法。文献[5]在逐步Ⅱ型混合截尾恒加寿命试验下,给出了指数分布竞争失效产品未知参数及可靠性指标的极大似然估计和贝叶斯估计。文献[6]在逐步Ⅰ型混合截尾下,建立了威布尔产品恒加试验竞争失效模型,给出了模型参数的极大似然估计、渐近置信区间、贝叶斯估计和近似可信区间。
加速寿命试验的特点是把产品放在高于正常应力水平下进行试验,在获得失效数据后,利用产品寿命和应力水平之间的关系(加速模型),对产品在正常应力水平下的寿命特征进行统计推断。但在工程实际中,产品寿命和应力水平之间的关系不一定总是已知的,例如测试对象是新产品。在这种情形下,可考虑部分加速寿命试验(PALT)。PALT的统计分析不需要加速模型,它通过引入加速因子,将高应力水平下的寿命特征外推到正常应力水平下,进而对产品在正常应力水平下的寿命特征进行统计推断[7]。近年来PALT已被应用于产品的可靠性分析,见文献[7-10]。但上述PALT的统计推断方法仅适用产品只有一个失效机理的情况,而实际上很多产品包含多个失效机理。当产品具有多个竞争失效机理时,如何利用PALT研究其寿命特征的统计分析具有重要的理论意义和应用价值。鉴于此,本文将逐步混合截尾方式应用于加速寿命试验,在逐步Ⅰ型混合截尾下,讨论Pareto分布竞争失效产品恒定应力部分加速寿命试验的统计推断问题。 文中给出了模型参数及加速因子的极大估计(MLE)和贝叶斯估计(BE)。利用Bootstrap方法及贝叶斯理论分别获得了模型参数的Bootstrap置信区间、最高后验概率密度(HPD)置信区间。最后利用Monte Carlo方法给出数值例子,比较了参数的MLE和BE的优劣性,并讨论了样本量和分配比例对估计精度的影响。
1 基本假设和模型描述选择2个应力水平S0<S1,其中S0为正常应力水平,S1为加速应力水平。基本假设如下:
1) 产品失效由且仅由2个失效机理之一引起。T1和T2分别代表机理1和机理2的发生时间,且它们相互独立,产品的寿命T=min(T1,T2)。
2) 在应力水平S0下,机理j(j=1,2)的发生时间服从Pareto分布,其可靠度函数和失效率函数分别为
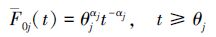
|
(1) |
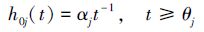
|
(2) |
式中,θj(θj>0)是尺度参数,αj(αj>0)是形状参数且已知。
3) 在应力水平S1下,机理j(j=1,2)的失效率函数为
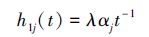
|
(3) |
式中,λ(λ>1)是加速因子。
根据失效率函数和可靠度函数的关系,可得应力S1下机理j(j=1,2)的可靠度函数为
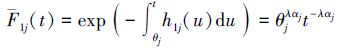
|
(4) |
逐步Ⅰ型混合截尾恒定应力部分加速寿命试验模型可描述如下:从n个具有上述失效机理的产品中,选取n0=n(1-r),0<r<1)个产品放在S0下进行寿命试验,剩余的n1=nr个产品放在S1下进行试验,r称为分配比例。在试验过程中,应力水平保持不变。预先设定失效数m<min(n0,n1)和时间τ,在应力水平Si(i=0,1)下同时进行如下试验:观测到第一个失效时刻ti1时,从剩下的ni-1个未失效产品中随机移走Ri1个。类似地,在第二个失效时刻ti2,从剩余的ni-2-Ri1个未失效产品中随机移除Ri2个,试验继续。若第m个失效时刻tim出现在时刻τ之前,则试验在时刻tim终止,并将剩下的Rim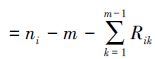

情形1 ti1<ti2<…<tim<τ;
情形2 ti1<ti2<…<tiJi<τ<ti(Ji+1)<ti(Ji+2)<…<tim。
令Di代表应力水平Si(i=0,1)下时刻τ之前的总失效数。那么,在情形1下Ti*=tim,Di=m,在情形2下Ti*=τ,Di=Ji。在时刻Ti*移走的产品数为Ri*=ni-Di-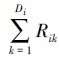
若观测样本记为(ti1,ci1),(ti2,ci2),…,(tiDi,ciDi),其中cil∈{1,2},l=1,2,…,Di为应力水平Si下引起第l个失效的机理编号,则在应力水平Si(i=0,1)下由机理j(j=1,2)引起的失效样本的似然函数为
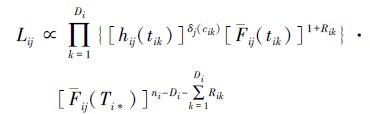
|
(5) |
式中,δj(cil)=1,当cil=j,δj(cil)=0,其他,j=1,2。Rik(i=0,1;k=1,2,…,Di)为应力水平Si下第k次失效后移走的产品数。将(1)~(4)式分别代入(5)式,可得到应力水平S0和S1下机理j(j=1,2)引起的失效样本似然函数为
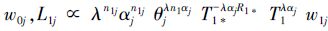

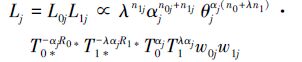
|
由于机理1和机理2的发生时间相互独立,所以全似然函数为
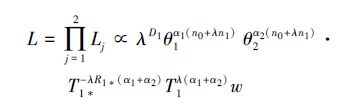
|
(6) |
式中,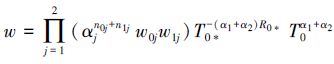
首先讨论参数的极大似然估计。对(6)式两边取对数得
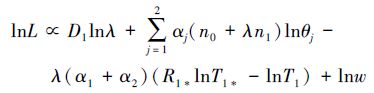
|
(7) |
进一步对(7)式分别关于λ和θj(j=1,2)求导并令其等于零,可得
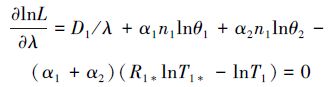
|
(8) |

|
(9) |
将(8)、(9)式联立,可得θj及λ的极大似然估计分别为
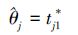
|
(10) |
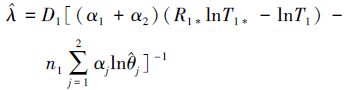
|
(11) |
式中,tj1*是由机理j(j=1,2)引起的第一个失效时间。
下面利用Bootstrap方法来构造参数的Bootstrap置信区间,具体步骤如下:
1) 利用原始的逐步Ⅰ型混合截尾Pareto分布竞争失效产品恒定应力部分加速寿命试验的数据,计算λ,θ1,θ2的极大似然估计值,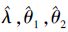
2) 将,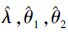

3) 重复步骤2)N次,将得到的所有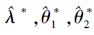

|
θj的置信度为1-γ的Bootstrap P置信区间是所有形如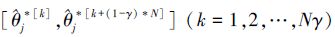
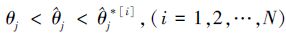
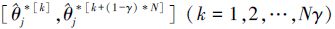
根据文献[11],分别针对λ,θj(j=1,2),基于步骤3)得到Bootstrap样本和统计量
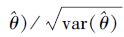
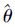
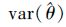
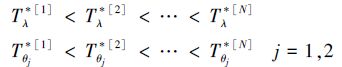
|
则λ,θj(j=1,2)的置信度为1-γ的Stu-t置信区间分别为
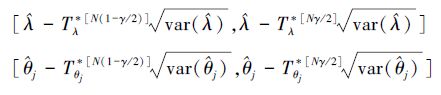
|
本节将利用贝叶斯方法来估计未知参数和加速因子。设λ,θ1,θ2的联合先验为无信息先验π(λ,θ1,θ2)∝1/λθ1θ2。结合(6)式,计算λ,θ1,θ2的联合后验密度函数为
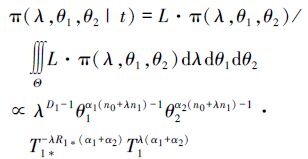
|
(12) |
式中,Θ={(λ,θ1,θ2)|λ>1,0<θj<tj1* (j=1,2)}。
将(12)式关于θ1,θ2积分得到λ的边际后验密度函数具有如下形式
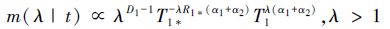
|
(13) |
因此,给定λ时,θ1,θ2的条件后验分布是幂律分布,密度函数分别为

|
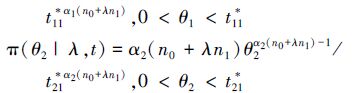
|
显然,无法根据(13)式求得平方损失函数下λ的贝叶斯估计。因此,采用自适应拒绝抽样法来解决该问题。我们首先证明λ的完全条件后验密度函数π(λ|θ1,θ2)是对数凹函数。给定θ1,θ2,对λ的完全条件后验密度函数取对数得

|
上式关于λ求二阶导数有∂2lnπ(λ|θ1,θ2)/∂λ2=-(D1-1)/λ2。显然上式右端小于0,故λ的完全条件后验密度函数是对数凹函数。下面通过自适应拒绝抽样法获得平方损失函数下λ,θj(j=1,2)的贝叶斯估计,并构造对应的HPD置信区间:
1) 给定θ1和θ2,利用自适应拒绝抽样法产生λ。
2) 利用生成的λ,分别产生服从后验分布密度函数π(θ1|λ,t)和π(θ2|λ,t)的θ1和θ2。
3) 重复步骤1)和步骤2) 1 000次,得到样本(λ(k),θ1(k),θ2(k)),k=1,2,…,1 000。则在平方损失函数下,λ,θj(j=1,2)的贝叶斯估计分别为
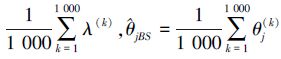
4) 将得到的所有λ(k),θ1(k),θ2(k))(k=1,2,…,1 000)分别按升序排列为(λ*[1]<λ*[2]<…<λ*[1 000])和(θj*[1]<θj*[2]<…<θj*[1 000])(j=1,2)。计算所有可能的置信区间[λ*[p],λ*[p+1 000(1-γ)]]和[θj*[p],θj*[p+1 000(1-γ)]](j=1,2;p=1,2,…,1 000-1 000(1-γ))。
5) 计算步骤4)中所得区间的宽度,其中宽度最小的区间即为参数的HPD置信区间。
4 数值模拟给定参数n、m、τ、αi、θi(i=1,2)、r和移走方案Rk1=Rk2=…Rk(m-1)=1,Rkm=n-2m+1(j=0,1)。根据以下步骤生成逐步Ⅰ型混合截尾Pareto分布竞争失效数据:
1) 分别产生4组逐步Ⅰ型截尾样本U11(0),U12(0),…,U1m(0);U21(0),U22(0),…,U2m(0); W11(1),W12(1),…,W1m(1); W21(1),W22(1),…,W2m(1),它们都来自均匀分布总体U(0,1)。
2) 对i=1,2和1≤j≤m,通过Uij(0)=1-θiαi t0ij-αi 计算t01j和t02j,并且把min(t01j,t02j)记为t
3) 对i=1,2和1≤j≤m,由Wij(1)=1-θiλαi t1ij-λαi 计算t11j和t12j,记min(t11j,t12j)为t1j*。若t1j*=t11j,记δ1j*=1;反之记δ1j*=2。
4) 若tim*<τ,则Di=m; 否则查找满足条件tiDi*<τ<ti(Di*+1) 的Di(i=0,1)。令tj(i)=tij*,δj(i)=δij*,R(i)=(Ri1,Ri2,…,RiDi),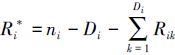
(t1(0),t2(0),…,tD0(0))和(t1(1),t2(1),…,tD1(1))分别为S0和S1下的逐步Ⅰ型混合截尾失效数据,对应的失效机理编号和移走方案分别为(δ1(0),δ2(0),…,δD0(0)),(R0(0),R*)和(δ1(1),δ2(1),…,δD1(1)),(R1(1),R*)。
为了研究样本总数和样本分配比例对估计的影响,给定初始值α1=0.2,α2=0.3,θ1=2.4,θ2=3,λ=1.8,τ=8,m=0.2n。根据上述算法,分别在r=0.4,0.5和0.6时模拟产生1 000组数据,并基于数据计算λ,θj(j=1,2)的(MLE)和(BE)。将2种估计的平均相对误差(ARE)和均方误差(MSE)列于表 1~表 3中,其中ARE和MSE的计算公式分别为

| n | 估计 | λ | θ1 | θ2 | |||
| ARE | MSE | ARE | MSE | ARE | MSE | ||
| 50 | MLE | 0.674 | 0.761 | 0.109 | 0.080 | 0.711 | 0.798 |
| BE | 0.299 | 0.330 | 0.098 | 0.056 | 0.324 | 0.751 | |
| 80 | MLE | 0.288 | 0.604 | 0.057 | 0.042 | 0.377 | 0.780 |
| BE | 0.275 | 0.303 | 0.046 | 0.024 | 0.273 | 0.733 | |
| 100 | MLE | 0.284 | 0.590 | 0.043 | 0.020 | 0.293 | 0.746 |
| BE | 0.272 | 0.280 | 0.037 | 0.016 | 0.264 | 0.715 | |
| 120 | MLE | 0.278 | 0.419 | 0.036 | 0.012 | 0.284 | 0.736 |
| BE | 0.225 | 0.194 | 0.030 | 0.011 | 0.252 | 0.624 | |
| 150 | MLE | 0.273 | 0.384 | 0.026 | 0.009 | 0.263 | 0.736 |
| BE | 0.104 | 0.050 | 0.024 | 0.007 | 0.237 | 0.487 | |
| 200 | MLE | 0.270 | 0.331 | 0.020 | 0.004 | 0.252 | 0.712 |
| BE | 0.0852 | 0.033 | 0.017 | 0.003 | 0.092 | 0.089 | |
| n | 估计 | λ | θ1 | θ2 | |||
| ARE | MSE | ARE | MSE | ARE | MSE | ||
| 50 | MLE | 0.419 | 0.601 | 0.071 | 0.060 | 0.404 | 0.789 |
| BE | 0.226 | 0.205 | 0.053 | 0.032 | 0.310 | 0.709 | |
| 80 | MLE | 0.286 | 0.562 | 0.047 | 0.032 | 0.271 | 0.778 |
| BE | 0.190 | 0.142 | 0.040 | 0.018 | 0.259 | 0.523 | |
| 100 | MLE | 0.278 | 0.483 | 0.038 | 0.019 | 0.270 | 0.751 |
| BE | 0.188 | 0.141 | 0.032 | 0.012 | 0.219 | 0.631 | |
| 120 | MLE | 0.276 | 0.409 | 0.030 | 0.016 | 0.266 | 0.715 |
| BE | 0.104 | 0.047 | 0.029 | 0.009 | 0.203 | 0.410 | |
| 150 | MLE | 0.272 | 0.354 | 0.025 | 0.008 | 0.257 | 0.695 |
| BE | 0.085 | 0.032 | 0.021 | 0.006 | 0.153 | 0.217 | |
| 200 | MLE | 0.267 | 0.318 | 0.018 | 0.004 | 0.249 | 0.545 |
| BE | 0.083 | 0.031 | 0.015 | 0.003 | 0.091 | 0.081 | |
| n | 估计 | λ | θ1 | θ2 | |||
| ARE | MSE | ARE | MSE | ARE | MSE | ||
| 50 | MLE | 0.352 | 0.691 | 0.066 | 0.052 | 0.378 | 0.732 |
| BE | 0.206 | 0.168 | 0.052 | 0.027 | 0.278 | 0.696 | |
| 80 | MLE | 0.286 | 0.535 | 0.040 | 0.019 | 0.266 | 0.717 |
| BE | 0.155 | 0.100 | 0.038 | 0.018 | 0.219 | 0.461 | |
| 100 | MLE | 0.274 | 0.469 | 0.037 | 0.015 | 0.265 | 0.702 |
| BE | 0.110 | 0.056 | 0.029 | 0.011 | 0.214 | 0.349 | |
| 120 | MLE | 0.273 | 0.395 | 0.029 | 0.009 | 0.260 | 0.685 |
| BE | 0.085 | 0.032 | 0.024 | 0.008 | 0.186 | 0.325 | |
| 150 | MLE | 0.268 | 0.338 | 0.023 | 0.007 | 0.253 | 0.657 |
| BE | 0.083 | 0.031 | 0.017 | 0.005 | 0.092 | 0.081 | |
| 200 | MLE | 0.266 | 0.315 | 0.016 | 0.003 | 0.196 | 0.541 |
| BE | 0.082 | 0.031 | 0.015 | 0.003 | 0.029 | 0.011 | |
从表 1~表 3可以看出,参数的MLE和BE的ARE和MSE均随样本量增大而变小;而贝叶斯估计的ARE和MSE均比MLE的ARE和MSE小,可见参数的BE比MLE更精确。另一方面,样本分配比例r与2种估计所对应的ARE和MSE呈负相关关系。为进一步比较区间估计的效果,从n=80时模拟产生的1 000组样本中选取一组列于表 4。根据前文假设,每个应力水平下的预期失效数m=16。
| 应力水平S0下 | 应力水平S1下 | ||
| 失效时间 | 机理编号 | 失效时间 | 机理编号 |
| 2.405 | 1 | 2.901 | 1 |
| 2.456 | 1 | 2.986 | 1 |
| 2.822 | 1 | 2.995 | 1 |
| 3.205 | 1 | 3.347 | 2 |
| 4.595 | 2 | 3.362 | 2 |
| 4.781 | 2 | 3.557 | 2 |
| 4.818 | 2 | 3.668 | 2 |
| 5.461 | 2 | 4.237 | 1 |
| 7.012 | 1 | 4.707 | 2 |
| 7.170 | 1 | 4.771 | 2 |
基于表 4的数据,分别计算λ,θ1,θ2的MLE、BE以及2种区间估计的上、下限列于表 5。由于θ1和θ2的MLE分别是由机理1和机理2引起的第一个失效时间,所以对应的Bootstrap样本值都大于初始值并且相对集中。
由表 5可知,参数的BE更接近初始值。由于参数λ的本身是正数,所以表 5中λ的Stud-t置信区间的下限取为0。比较参数的Stud-t置信区间和HPD置信区间的长度,发现HPD置信区间长度较小,Stud-t置信区间长度较大。这说明在相同的置信度95% 情形下,HPD置信区间优于Stud-t置信区间。
5 结论基于逐步Ⅰ型混合截尾恒定应力部分加速寿命下Pareto分布竞争失效产品的寿命数据,利用极大似然法和贝叶斯理论获得了分布参数和加速因子的MLE和BE。分别运用Bootstrap法和自适应拒绝抽样法得到了参数和加速因子的Stud-t置信区间HPD置信区间。最后,利用Monte Carlo方法给出数值例子,比较了参数的MLE和BE的优劣性,并讨论了样本量和分配比例对估计精度的影响。模拟计算表明,贝叶斯点估计比MLE更精确;参数及加速因子的MLE和BE的精度随着样本量和分配比例的增大而提高;在相同的置信度下,HPD置信区间优于Stud-t置信区间。
| [1] | Han D, Kundu D. Inference for a Step-Stress Model with Competing Risks for Failure from the Generalized Exponential Distribution under Type-I Censoring[J]. IEEE Trans on Reliability, 2015, 64(1): 31–43. DOI:10.1109/TR.2014.2336392 |
| [2] | Roy S, Mukhopadhyay C. Maximum Likelihood Analysis of Multi-Stress Accelerated Life Test Data of Series Systems with Competing Log-Normal Causes of Failure[J]. Journal of Risk and Reliability, 2015, 229(2): 119–130. |
| [3] | Xu A, Tang Y. Statistical Analysis of Competing Failure Modes in Accelerated Life Testing Based on Assumed Copulas[J]. Chinese Journal of Applied Probability, 2012, 28(1): 51–62. |
| [4] | Zhang X P, Shang J Z, Chen X, et al. Statistical Inference of Accelerated Life Testing with Dependent Competing Failures Based on Copula Theory[J]. IEEE Trans on Reliability, 2014, 63(3): 764–780. DOI:10.1109/TR.2014.2314598 |
| [5] | Shi Y, Jin L, Wei C, et al. Constant-Stress Accelerated Life Test with Competing Risks under Progressive Type-II Hybrid Censoring[J]. Advanced Materials Research, 2013, 712: 2080–2083. |
| [6] | Wu M, Shi Y, Sun Y. Inference for Accelerated Competing Failure Models from Weibull Distribution under Type-I Progressive Hybrid Censoring[J]. Journal of Computational and Applied Mathematics, 2014, 263: 423–431. DOI:10.1016/j.cam.2013.12.048 |
| [7] | Ali A Ismail. Likelihood Inference for a Step-Stress Partially Accelerated Life Test Model with Type-I Progressively Hybrid Censored Data from Weibull Distribution[J]. Journal of Statistical Computation and Simulation, 2014, 84(11): 2486–2494. DOI:10.1080/00949655.2013.836195 |
| [8] | Ali A Ismail. Inference for a Step-Stress Partially Accelerated Life Test Model with An Adaptive Type-Ii Progressively Hybrid Censored Data from Weibull Distribution[J]. Journal of Computational and Applied Mathematics, 2014, 260: 533–542. DOI:10.1016/j.cam.2013.10.014 |
| [9] | Abd-Elfattah A M, Hassan A S, Nassr S G. Estimation in Step-Stress Partially Accelerated Life Tests for the Burr TypeⅫ Distribution Using TypeⅠ Censoring[J]. Statistical Methodology, 2008, 5: 502–514. DOI:10.1016/j.stamet.2007.12.001 |
| [10] | Alaa H, Abdel H. Constant-Partially Accelerated Life Tests for Burr TypeⅫ Distribution with Progressive TypeⅪ Censoring[J]. Computational Statistics And Data Analysis, 2009, 53: 2511–2523. DOI:10.1016/j.csda.2009.01.018 |
| [11] | Balakrishnan N, Xie Q. Exact Inference for a Simple Step-Stress Model with TypeⅡ Hybrid Censored Data from The Exponential Distribution[J]. Journal of Statistical Planning and Inference, 2007, 137: 2543–2563. DOI:10.1016/j.jspi.2006.04.017 |
2. School of Electronic Engineering, Xi'an University of Posts and Telecommunications, Xi'an 710121, China


