2. 南京航空航天大学 机械结构力学及控制国家重点实验室, 江苏 南京 210016
随着材料技术和加工技术的不断发展, 薄壁结构在航空航天装备轻量化设计中的应用愈加广泛。然而由于薄壁结构本身的低刚度和低阻尼特性, 其在应用过程中很容易受外界干扰产生振动, 从而影响整体结构稳定性甚至对装备造成损坏[1]。由此可见, 薄壁结构的振动控制是其应用研究的重要组成部分。由于智能结构良好的传感、致动和控制性能以及压电材料优秀的机电耦合性能和与基体结构易结合性, 压电智能结构振动控制成为振动控制领域的研究热点。
在压电智能结构中, 压电材料被集成到基体结构中作为传感器和致动器。当基体结构产生振动时, 传感器采集振动信号并传递至控制器, 随后控制器根据相关控制算法生成控制信号并传递到致动器以控制结构振动。由此可见, 控制算法是压电智能结构振动控制中极为重要的一环。国内外学者对振动控制的控制算法亦非常重视, 并研究了经典控制理论和现代控制理论中的很多控制算法在振动控制方面的应用。Omidi和Mahmoodi[2]开发并比较了用于压电柔性梁振动控制的改良的速度反馈控制和位置反馈控制。Zhong等[3]在压电层合梁的振动控制中通过应用精细积分方法, 提高了振动分析和LQR控制中Riccati方程求解的计算精度和稳定性。Kapuria和Yasin[4]比较了LQR控制、LQG控制和速度反馈控制对压电层合智能梁振动控制的效果。针对压电悬臂梁的相位迟滞和延时问题, Qiu等[5]提出并开发了一种具有相移特性的滑模变结构控制并在试验中进行了验证。Dubay等[6]将有限元建模和模型预测控制相结合, 并将其应用于装有单杆柔性机械臂的振动控制。Marinaki等[7]提出并在压电层合梁振动控制中验证了多目标差分进化算法优化的模糊控制算法。Yang等[8]提出了一种弯曲型压电致动结构, 并采用神经网络预测控制方法设计了悬臂梁的主动振动控制系统。
外界扰动是引起薄壁结构振动的主要原因之一, 然而在上述控制器设计中并没有考虑扰动的影响。如果引起结构振动的扰动量能够在控制回路系统中被消除, 那么该系统将会变得更加稳定且易于控制。Müller 和Lückel[9]提出并开发了一种使用proportional integral(PI)观测器观测系统扰动并反馈到控制回路以抵消扰动对系统的影响的抗扰控制算法。Zhang等[10-11]研究了使用generalized proportional integral(GPI)观测器的抗扰控制, 并将其应用在压电层合梁的振动控制中。由于GPI观测器能够在频率已知的情况下很准确地观测周期性扰动并且反馈到控制回路, 故基于GPI观测器的抗扰控制能够很好地控制由频率已知的扰动引起的振动。然而对于由频率未知周期性扰动或非周期性扰动引起的振动, 此抗扰控制算法的振动控制性能则有所下降。
为了能够在扰动频率未知或者随机变化的情况下更好地控制智能结构的振动, 本文提出并开发了一种双重积分模型的抗扰控制算法并将其用于压电层合梁的振动控制。该算法的关键在于提出了一种双重积分状态空间模型, 并依据此模型来设计观测器和抗扰控制器。此双重积分模型的特殊结构使系统更容易解耦, 提高了观测器及控制器设计的灵活性。在此双重积分状态空间模型基础上设计的观测器能够快速准确地观测系统的广义扰动并通过抗扰控制器将其反馈到系统中来控制振动。最后, 通过压电层合梁的振动控制仿真算例对这种双重积分模型的抗扰控制算法进行了验证, 并与GPI观测器抗扰控制算法的控制效果进行了比较。仿真结果表明, 该双重积分模型抗扰控制算法能够有效地控制由频率未知或者随机变化的扰动引起的振动, 且其振动控制性能优于使用GPI观测器的抗扰控制算法。
1 动力学模型由于控制算法设计需要, 首先建立压电层合结构的动力学模型。运用有限元方法和Hamilton原理, 可以得出压电层合结构的动力学有限元模型[12]
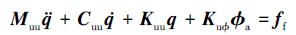
|
(1) |
式中,Muu、Cuu、Kuu、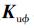


|
(2) |
式中,
为了便于控制器的设计, 需要得到整个系统的状态空间模型。由(1)式和(2)式可推导出系统原始的状态空间模型如下:
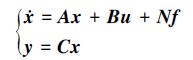
|
(3) |
式中状态向量x、输入向量u、物理扰动f和输出向量y与(1)、(2)式中各向量关系为:
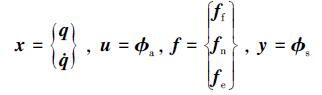
|
(4) |
fn与fe分别代表由系统非线性部分和模型误差引起的扰动。此外, 由)(1)和(2)式可计算出系统矩阵A、系统输入矩阵B、物理扰动输入矩阵N和系统输出矩阵C如下

|
(5) |
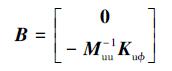
|
(6) |
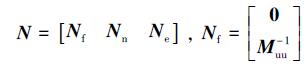
|
(7) |

|
(8) |
式中,Nf、Nn和Ne分别为外力扰动输入矩阵、非线性扰动输入矩阵和模型误差扰动输入矩阵。其中由于系统非线性和模型误差未知, 故Nn和Ne无法计算, 导致非线性扰动和模型误差扰动不能被观测。
由(5)式不难看出原始状态空间模型中状态变量耦合性较强, 不利于观测器和控制器的设计。为了观测系统的非线性扰动和模型误差扰动, 并且提高设计观测器和控制器的灵活性, 需要将原始状态空间模型进行转换。首先引入新的状态向量z:
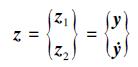
|
(9) |
对(9)式求时间的一阶导并将(3)式、(6)式、(8)式代入其中可得
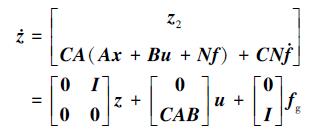
|
(10) |
式中定义fg为广义扰动向量, 并表示为
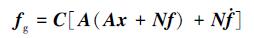
|
(11) |
由(9)、(10)式中系统输入u和系统输出y之间的关系可得出以z为状态向量的状态空间模型如下

|
(12) |
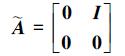
|
(13) |
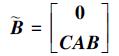
|
(14) |
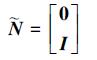
|
(15) |
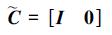
|
(16) |
结合(12)~(16)式可知输出y为输入u的双重积分, 故定义(12)式中的状态空间模型为双重积分状态空间模型。不难看出, (3)式中的原始状态空间模型和(12)式中双重积分状态空间模型都描述了系统输入u和系统输出y的关系, 但明显(12)式中系统更容易解耦。利用双重积分状态空间模型设计观测器与控制器, 使经典设计理论和现代设计理论均能用于观测器和控制器的设计, 提高了设计的灵活性。由(11)式可看出, 广义扰动fg包含了物理扰动和原始系统的状态变量, 简化了系统模型结构, 这也是双重积分状态空间模型易解耦的原因之一。在抗扰控制算法中, 使用观测器观测广义扰动并反馈到控制回路不仅可以抵消物理扰动对系统产生的影响, 而且原始状态空间模型的状态变量也随广义扰动反馈回系统对系统进行控制。此外, 假设原始状态空间模型状态向量x和输出向量y的维数分别为n和m, 由有限元模型的节点数目所决定的n远大于由输出变量个数所决定的m。所以状态空间模型的维数从n降至2m, 极大地减少了控制算法的计算量。
2.2 观测器设计 2.2.1 扩展系统为了能够观测广义扰动, 我们引入新的状态向量v来近似广义扰动fg。随后将状态向量v加入双重积分状态空间模型成为扩展系统并以此系统设计观测器。首先假设广义扰动fg和状态向量v的关系为[10-11]

|
(17) |
式中,Hv和Δ分别为fg的线性部分和残余误差部分, H和V分别为扰动输出矩阵和扰动系统矩阵。通常Δ足够小且可忽略[9], 则fg可近似表示为:
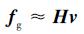
|
(18) |
为了使Hv能够逼近fg, 可假设v由傅立叶级数或泰勒级数中的若干基本项组成。显然, H和V的值由v中基本项的组合决定。基本项可根据fg的动态特性来选择, 例如GPI观测器中假设v由常数项和与扰动频率相同的正/余弦项组成[10]。由于本文所针对的扰动为频率未知甚至随机变化的扰动, 故设定v由不含任何动态信息的常数项组成, 即PI观测器[10, 14]中对扰动的设定
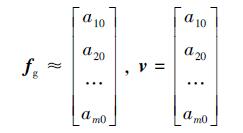
|
(19) |
将(19)式代入(17)、(18)式可计算H、V
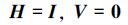
|
(20) |
将(17)式代入(12)式可得扩展系统如下
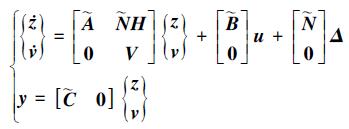
|
(21) |
由(21)式可看出在扩展系统中以状态向量的形式来描述广义扰动fg。故可根据此扩展系统设计状态观测器, 广义扰动fg的观测值可由状态向量v的观测值计算而得。
2.2.2 观测器设计根据Luenberger观测器结构, (21)式中扩展系统的观测器可建立如下
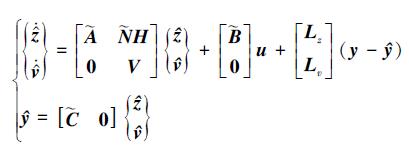
|
(22) |
式中, 矩阵Lz和Lv代表观测器增益, 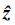

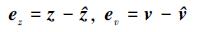
|
(23) |
由(21)~(23)式可得观测器观测误差模型

|
(24) |

|
(25) |
对于(24)、(25)式中的误差模型, 如果矩阵Ab的特征值都处于复平面的左半平面, 则误差模型是稳定的并且ez、ev将收敛于零, 即
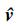
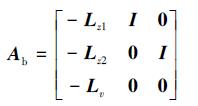
|
(26) |
式中,Lz1和Lz2为Lz的上半部分和下半部分
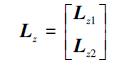
|
(27) |
计算Ab的特征多项式如下

|
(28) |
为了使设计更加直观, 需要对观测器进行解耦并使用极点配置法。设定Lz1和Lz2和Lv为对角矩阵

|
(29) |
将(29)式代入(28)式, 则Ab的特征多项式为
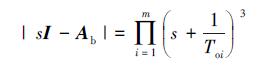
|
(30) |
由(30)式可知Ab有m个三重特征根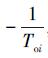
为了消除广义扰动对系统的影响并且使系统稳定, 需要将所观测的广义扰动和状态变量通过抗扰控制器反馈回系统以控制智能结构的振动。故设定系统控制向量u为

|
(31) |
式中,Kz和Kv分别为和的增益矩阵, Bcr-为矩阵
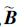
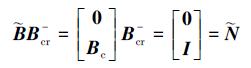
|
(32) |
Bcr-存在的充分必要条件为Bc为行满秩矩阵, 通常此条件在振动系统中是成立的。将(31)、(32)式代入(12)式可得到双重积分状态空间模型的闭环系统为
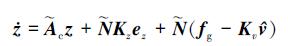
|
(33) |
式中,

|
(34) |
结合(18)式和(33)式可看出若Kv=H则在闭环系统中广义扰动可被抵消, 此时闭环系统可化为
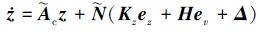
|
(35) |
当观测器收敛时, ez、ev和Δ均为有界的, 所以如果

|
(36) |
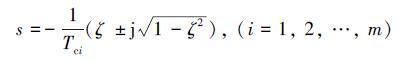
|
(37) |
式中,j表示单位虚数, 若对于i=1, 2, …, m都有Tci>0则闭环系统渐进稳定。此时控制器增益矩阵Kz为

|
(38) |
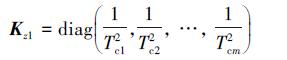
|
(39) |

|
(40) |
由(36)式可知闭环系统被解耦为m个并联的经典二阶系统, 其中ζ为阻尼比, Tci为第i个二阶系统的增益参数。根据经典二阶系统的控制规律, ζ=1时二阶系统为临界阻尼状态, 系统输出无震荡且响应速度快。此外, Tci与第i个二阶系统的调节时间成正比, 因此Tci(i=1, 2, …, m)的最大值越小, 闭环系统的响应速度越快。将(17)、(23)、(31)式代入(3)、(22)、(24)式可推导出抗扰控制在原始状态空间下的闭环系统如下:

|
(41) |
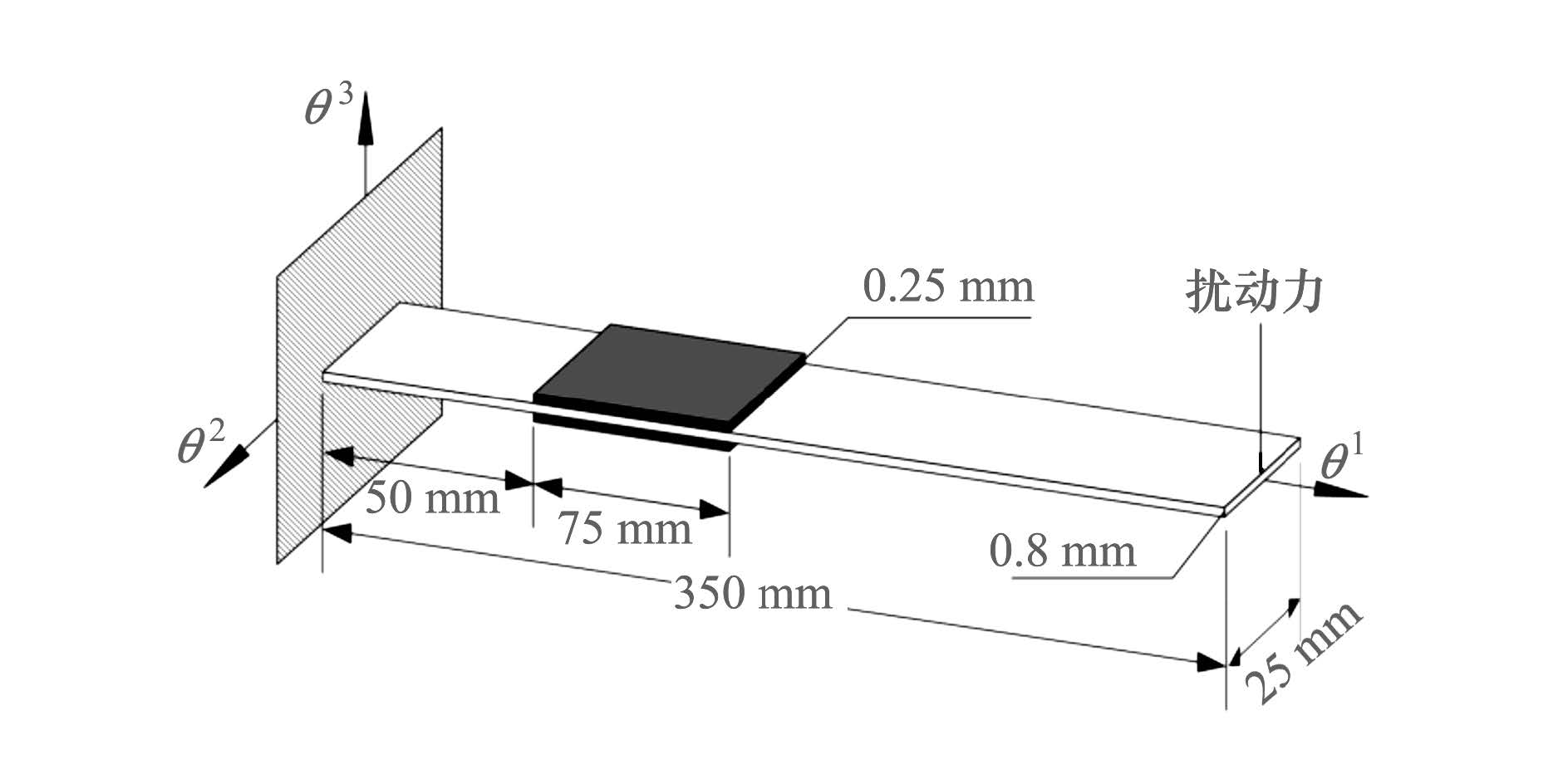
本文以压电层合悬臂梁为例对双重积分模型抗扰控制算法进行仿真验证。如图 1所示, 2个压电片并列贴合在悬臂梁的上下两面, 一个外力扰动施加在悬臂梁末端的中点。2个压电片极化方向与θ3轴平行但方向相反, 故两压电片可分别作为传感器和致动器。悬臂梁的材料为钢, 其材料属性分别为杨氏模量Y=210 GPa、密度ρ=7 900 kg/m3、泊松比ν=0.3。压电片材料为PZT, 其材料属性分别为杨氏模量Y=67 GPa、密度ρ=7 800 kg/m3、泊松比ν=0.3、压电常数d31=d32=-2.1×10-10 C/N、介电常数ε=2.13×10-8 F/m。
|
| 图 1 压电层合悬臂梁示意图 |
根据线性一阶剪切变形理论, 采用八节点Serendipity族壳单元和14×1网格建立该压电层合悬臂梁的有限元模型。为了验证当前有限元模型准确性, 在ANSYS中建立图 1压电层合梁的有限元模型, 对两者进行模态分析并比较其特征频率。如表 1所示, 通过对比发现两模型前5阶特征频率差值较小, 说明当前有限元模型较为准确。
| 模型及差值 | 一阶 | 二阶 | 三阶 | 四阶 | 五阶 |
| 当前模型 特征频率/Hz | 6.15 | 33.72 | 97.37 | 166.07 | 175.06 |
| Ansys模型 特征频率/Hz | 6.08 | 33.35 | 95.23 | 162.70 | 174.47 |
| 差值百分比/% | 1.15 | 1.11 | 2.25 | 2.07 | 0.34 |
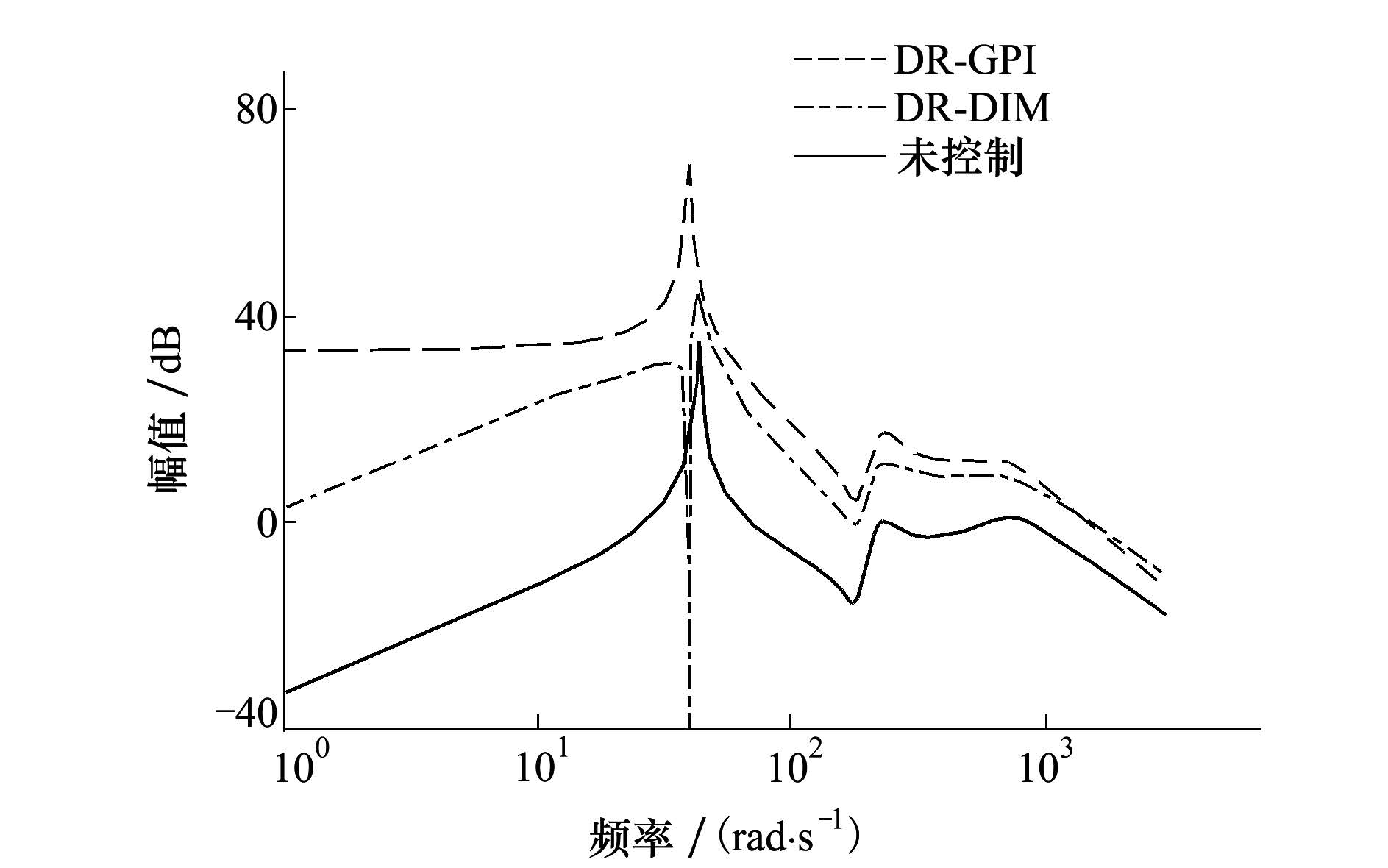
为了分析双重积分模型的抗扰控制算法对于不同频率扰动的振动控制的表现, 需要对使用双重积分模型抗扰控制的压电层合梁进行幅频响应分析。此外, 加入了使用原始模型GPI观测器的抗扰控制的幅频响应以进行比较。设置GPI观测器频率信息与压电层合梁的一阶特征频率相等, 即角频率为ω=38.65 rad/s。如图 2所示, DR-GPI和DR-DIM两条曲线分别代表使用原始模型GPI观测器的抗扰控制和双重积分模型抗扰控制的幅频响应曲线。2种抗扰控制算法均能不同程度地降低幅频响应, 即控制压电层合梁的振动。此外, 对于低频扰动引起振动的控制效果优于高频扰动。这主要是由于在高频情况下观测扰动的相位滞后对于观测误差的影响比低频情况大得多, 导致高频扰动不能被准确地消除。由于双重积分模型下的观测器收敛速度更快, 故观测误差更小, 进而使双重积分模型抗扰控制的振动控制效果优于使用原始模型GPI观测器的抗扰控制。图 2中使用GPI观测器的抗扰控制的频响曲线很好地展示了GPI观测器的特性, 即能够准确观测某个设定频率的扰动, 故使用GPI观测器的抗扰控制能够极大程度地控制由其设定频率或相近频率的扰动所引起的振动。
|
| 图 2 未控制与使用不同抗扰控制的压电层合梁幅频响应图 |
在2个振动控制仿真算例中, 分别采取2种扰动作为压电层合梁的激励源。第一个算例采取频率为压电层合梁一阶特征频率的周期性扰动, 第二个算例使用频率在1~10 Hz内随机变化的非周期性扰动, 分别验证双重积分模型抗扰控制算法对于控制由未知频率周期性扰动和频率随机变化非周期性扰动引起的振动的有效性。此外, 还加入了使用原始模型GPI观测器的抗扰控制进行比较。GPI观测器所设定频率信息与压电层合梁一阶特征频率相同, 即角频率为ω=38.65 rad/s。
3.3.1 一阶特征频率扰动在第一个算例中, 激励源为频率与压电层合梁一阶特征频率相同的正弦外力扰动。算例仿真结果如图 3所示, 图 3a)~c)分别为压电传感器输出电压、压电致动器输入电压、扰动观测相对误差。

|
| 图 3 一阶特征频率扰动激励下的未控制和使用不同抗扰控制的压电层合梁响应 |
如图 3a)所示, DR-GPI和DR-DIM 2条曲线分别代表使用原始模型GPI观测器的抗扰控制和双重积分模型抗扰控制的压电层合梁传感器电压输出曲线。2种不同的抗扰控制算法均能不同程度地控制压电层合梁的振动, 其中双重积分模型抗扰控制的效果最佳。如图 3c)所示, 虽然频率信息与扰动频率一致, 但ω=38.65 rad/s的GPI观测器需要一定时间收敛扰动观测误差。因此, 在其观测误差未收敛至零附近前, 使用GPI观测器的抗扰控制算法并不能很好地控制振动。使用双重积分模型的观测器的快速收敛速度使其能很快地收敛观测误差, 进而使双重积分模型抗扰控制能够更好地控制振动。
3.3.2 随机变化频率扰动第二个算例中, 外力扰动频率在1~10 Hz范围内随机变化。算例仿真结果如图 4所示, 图 4a)~c)分别为压电传感器输出电压、压电致动器输入电压、扰动观测相对误差。

|
| 图 4 随机变化频率扰动激励下的未控制和使用不同抗扰控制的压电层合梁响应 |
由图 4a)可知, 双重积分模型抗扰控制算法对压电层合梁的振动控制效果最好。由于扰动频率随机变化, GPI观测器不能通过设置与扰动相同的频率信息来获得与扰动一致的动态特性, 故GPI观测器观测误差增大。较大的观测误差导致扰动不能准确地反馈到闭环回路, 使振动控制效果变差。而使用双重积分模型的观测器的快速响应特性使其能够快速准确地跟踪扰动信号, 并将扰动观测值反馈到抗扰控制器以控制振动。如图 4c)所示, GPI观测器的相对观测误差均达到50%以上并大于上一算例中误差, 而双重积分模型的观测器的相对观测误差则继续在零附近小范围波动。
4 结 论针对受频率未知或随机变化的扰动激励的智能结构振动控制, 本文提出并开发了一种双重积分模型的抗扰控制算法。在该抗扰控制算法中, 使用了一种双重积分系统状态空间模型来设计观测器和抗扰控制器。此双重积分状态空间模型将外力扰动、系统非线性部分、模型误差等物理扰动和部分原始系统状态变量归纳为一种广义扰动, 简化了系统模型结构并赋予了双重积分模型良好的解耦性, 进而提高了观测器及控制器设计的灵活性。通过极点配置法, 设计了一个具有快速收敛速度的PI观测器, 从而使广义扰动和双重积分模型的状态变量能够被该PI观测器快速准确地观测并通过抗扰控制器反馈到系统形成闭环回路。随后, 在压电层合梁的振动控制仿真中验证了这种双重积分模型抗扰控制算法的有效性并且与使用GPI观测器的抗扰控制算法进行了比较。
仿真结果表明, 双重积分模型抗扰控制算法能够有效控制由频率未知或随机变化的扰动引起的振动。此外, 由于使用双重积分模型设计的观测器能够更快速、准确地观测扰动, 双重积分模型抗扰控制算法的振动控制性能优于使用GPI观测器的抗扰控制算法。
| [1] | Wang Z, Qin X, Yang H T Y. Active Suppression of Panel Flutter with Piezoelectric Actuators Using Eigenvector Orientation Method[J]. Journal of Sound and Vibration, 2012, 331(7): 1469–1482. DOI:10.1016/j.jsv.2011.11.015 |
| [2] | Omidi E, Mahmoodi S N. Vibration Control of Collocated Smart Structures Using H∞ Modified Positive Position and Velocity Feedback[J]. Journal of Vibration and Control, 2016, 22(10): 2434–2442. DOI:10.1177/1077546314548471 |
| [3] | Zhong M F, Deng Z C, Wang Z J. Finite Element Analysis and Vibration Control of Piezoelectric Laminated Plates Based on Precise Integration[J]. Journal of Northwestern Polytechnical University, 2010, 28(1): 123–128. |
| [4] | Kapuria S, Yasin M Y. Active Vibration Control of Piezoelectric Laminated Beams with Electroded Actuators and Sensors Using an Efficient Finite Element Involving an Electric Node[J]. Smart Materials and Structures, 2010, 19(4): 045019. DOI:10.1088/0964-1726/19/4/045019 |
| [5] | Qiu Z C, Han J D, Zhang X M, et al. Active Vibration Control of A Flexible Beam Using a Non-Collocated Acceleration Sensor and Piezoelectric Patch Actuator[J]. Journal of Sound and Vibration, 2009, 326((3/4/5): 438–455. |
| [6] | Dubay R, Hassan M, Li C, et al. Finite Element Based Model Predictive Control for Active Vibration Suppression of a One-Link Flexible Manipulator[J]. ISA Transactions, 2014, 53(5): 1609–1619. DOI:10.1016/j.isatra.2014.05.023 |
| [7] | Marinaki M, Marinakis Y, Stavroulakis G E. Fuzzy Control Optimized by a Multi-Objective Differential Evolution Algorithm for Vibration Suppression of Smart Structures[J]. Computers & Structures, 2015, 147: 126–137. |
| [8] | Yang Z C, Wang W, Gu Y S, et al. Smart Structure Vibration Control Using a New Bending Type of Piezoelectric Stack Actuator[J]. Journal of Vibration & Shock, 2009, 28(9): 130–134. |
| [9] | Müller P C, Lückel J. Optimal Multivariable Feedback System Design with Disturbance Rejection[J]. Problems of Control and Information Theory, 1977, 6(3): 211–227. |
| [10] | Zhang S Q, Li H N, Schmidt R, et al. Disturbance Rejection Control for Vibration Suppression of Piezoelectric Laminated Thin-Walled Structures[J]. Journal of Sound and Vibration, 2014, 333(5): 1209–1223. DOI:10.1016/j.jsv.2013.10.024 |
| [11] | Zhang S Q, Schmidt R, Müller P C, et al. Disturbance Rejection Control for Vibration Suppression of Smart Beams and Plates under A High Frequency Excitation[J]. Journal of Sound and Vibration, 2015, 353: 19–37. DOI:10.1016/j.jsv.2015.05.018 |
| [12] | Zhang S Q, Schmidt R. Large Rotation FE Transient Analysis of Piezolaminated Thin-Walled Smart Structures[J]. Smart Materials and Structures, 2013, 22(10): 105025. DOI:10.1088/0964-1726/22/10/105025 |
| [13] | Zhang S Q, Schmidt R. Static and Dynamic FE Analysis of Piezoelectric Integrated Thin-Walled Composite Structures with Large Rotations[J]. Composite Structures, 2014, 112: 345–357. DOI:10.1016/j.compstruct.2014.02.029 |
| [14] | Söffker D, Yu T J, Müller P C. State Estimation of Dynamical Systems with Nonlinearities by Using Proportional-Integral Observer[J]. International Journal of Systems Science, 1995, 26(9): 1571–1582. DOI:10.1080/00207729508929120 |
2. State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China


