2. 北京强度环境研究所可靠性与环境工程技术重点实验室, 北京 100076
经过逾半个世纪的发展, 有限元法 (FEM) 在科学研究及解决工程问题方面都得到了广泛应用。但是, 随着科学技术的发展, 有限元法越来越多地被应用于解决复杂问题, 其缺点与不足也越来越显著。首先, 有限元法将无限自由度的问题域离散为有限自由度使总体刚度矩阵偏“硬”而位移解偏小。其次, 常规有限元由于无法处理畸形网格, 其在大变形、塑性力学计算等方面表现无力。最后, 常规有限元法在使用简单低阶单元计算大型复杂结构时表现为计算精度不足, 而采用精度更高的高阶单元时又表现为计算量过大, 计算效率较低。
Liu和Nguyen等将有限元法 (FEM) 与应变光滑技术相结合提出了光滑有限元法 (S-FEM)[1]并应用于二维线弹性分析领域, 发现S-FEM在提供更加稳定、精确的数值解的同时打破了FEM中等参元内角不能大于180°的限制, 单元可以采用任意多边形使问题域的划分方式更加复杂多样。
根据光滑域划分方式的不同, 提出了多种S-FEM子方法并广泛应用。Liu和Daiy等提出了单元内划分光滑域的光滑子域有限元法 (CS-FEM) 并应用于求解弹性力学[2-4]问题, 与FEM比较发现CS-FEM的数值解更加稳定、精确并且在相同精度的条件下其计算效率更高。Dai和Liu等将任意多边形单元与CS-FEM相结合提出nCS-FEM并应用于弹性力学问题得到了比较精确的数值解[5]。其后又提出了基于节点划分光滑域的光滑节点域有限元法 (NS-FEM)[6], 发现其刚度矩阵偏软可得到问题域位移解的上限。
近年来, 基于单元边划分光滑域的光滑边域有限元法 (ES-FEM) 被提出来并应用于静力学及振动力学研究中[7]。发现与其他S-FEM相比,ES-FEM具有更佳的稳定性和精确性。随后, Nguyen和Liu又将ES-FEM算法与任意多边形单元相结合提出了nES-FEM方法并应用于求解二维线弹性力学问题, 得到了比nSFEM更为精确的数值解[8]。
本文研究了S-FEM算法的基本理论, 并推导了ES-FEM的光滑应变矩阵和刚度矩阵表达式, 利用C++语言编制了ES-FEM、CS-FEM和FEM等多种有限元算法程序, 结合Intel数学函数库MKL中的并行运算技术对悬臂梁模型和带孔板模型进行了分析对比研究。
1 光滑边域有限元法 1.1 基本理论与FEM相同, S-FEM也是通过建立形函数创建问题域的位移场
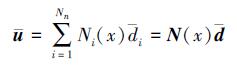
|
(1) |
式中, u为位移向量, N(x) 为形函数矩阵, d为单元节点位移向量。
利用应变光滑技术创建光滑应变场, 光滑应变场可通过修正相容应变场获得, 也可通过对位移场求导得到
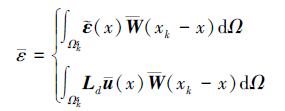
|
(2) |
式中, 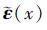
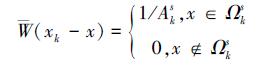
|
(3) |
式中, Aks为光滑域的面积。通常相容应变场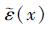
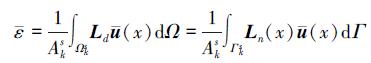
|
(4) |
式中, Γks为光滑域Ωks的边界, Ln(x) 为单位外法线向量矩阵:
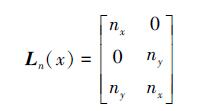
|
(5) |
式中, nx、ny为Ln(x) 的x轴和y轴方向分量。
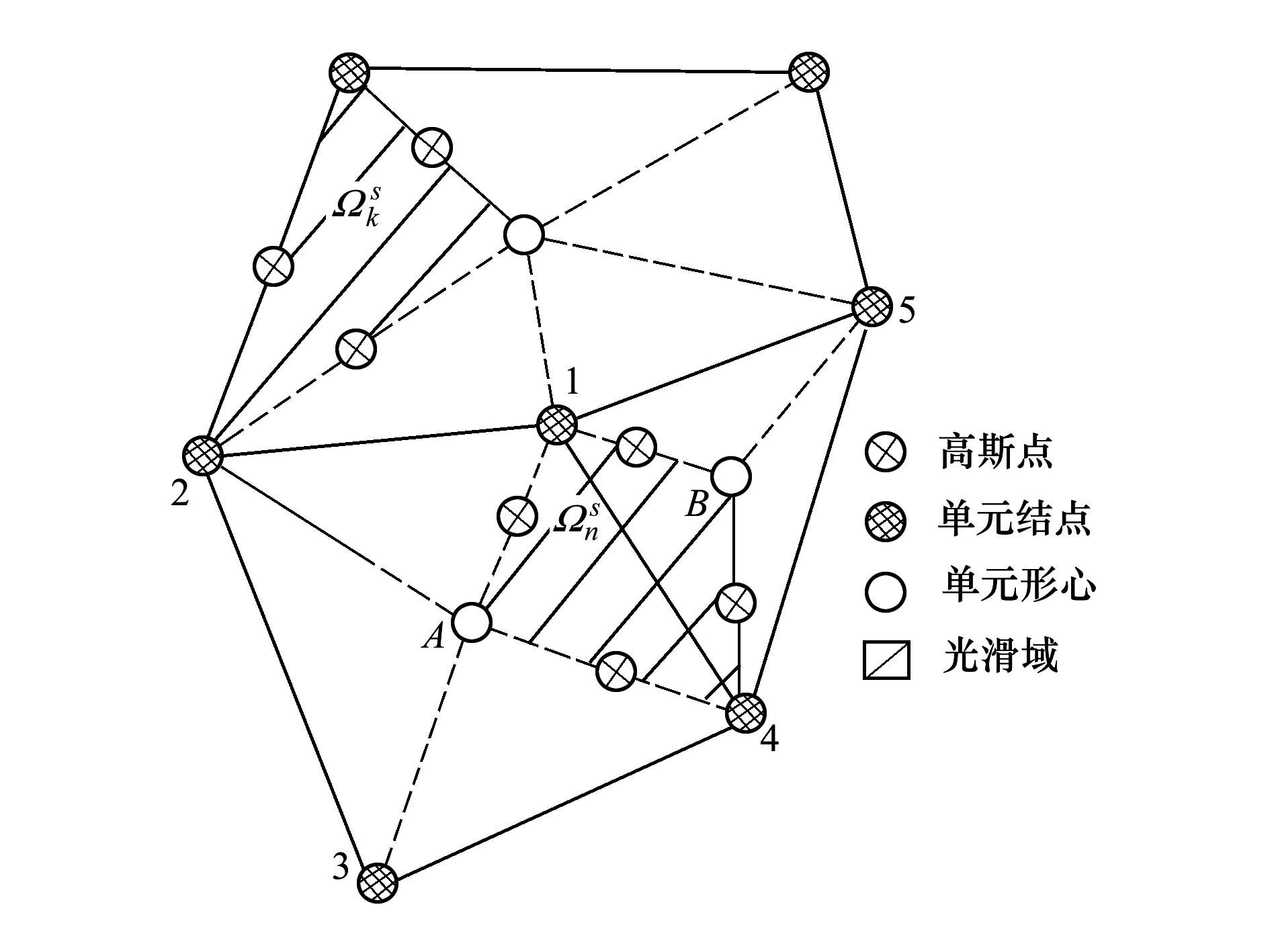
ES-FEM以单元边为基准划分光滑域, 其划分方法如图 1所示:
|
| 图 1 ES-FEM光滑域划分示意图 |
光滑域是由单元边上的2个结点与相邻单元的形心点连接而成。假设单元边总数为Neg, 光滑域总数为Ns。因为单元边与光滑域的一一对应关系, 所以有:
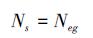
|
(6) |
将 (1) 式带入 (4) 式可得:
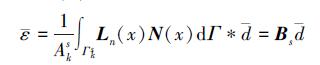
|
(7) |
式中, Bs为光滑域几何矩阵, 可对光滑边界进行形函数线积分得到:
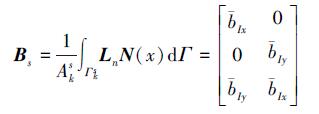
|
(8) |
式中
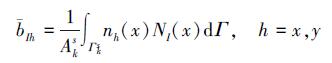
|
(9) |
S-FEM的总体平衡方程可由光滑Garlerkin弱化形式得到:
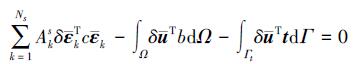
|
(10) |
式中, b为面域体力向量, t为边界牵引力向量。将 (1) 式和 (7) 式带入 (10) 式并化简可得:
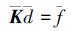
|
(11) |
式中,K为光滑刚度矩阵:
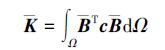
|
(12) |
综上可知, S-FEM计算过程中无须进行坐标映射, 可使用任意形状的单元, 避免了单元畸变, 降低了对网格质量的要求; 并且无须对形函数求导, 降低了对形函数连续性的要求。
1.2 形函数的确定ES-FEM的形函数取线性函数值, 故可采用一阶高斯积分方法求几何矩阵Bs。如图 1所示各点的形函数值如表 1所示:
| 编号 | Node1 | Node2 | Node3 | Node4 | Node5 | 点属性 |
| 1 | 1 | 0 | 0 | 0 | 0 | 场结点 |
| 2 | 0 | 1 | 0 | 0 | 0 | 场结点 |
| 3 | 0 | 0 | 1 | 0 | 0 | 场结点 |
| 4 | 0 | 0 | 0 | 1 | 0 | 场结点 |
| 5 | 0 | 0 | 0 | 0 | 1 | 场结点 |
| A | 1/4 | 1/4 | 1/4 | 1/4 | 0 | 单元形心 |
| B | 1/3 | 0 | 0 | 1/3 | 1/3 | 单元形心 |
| g1 | 5/8 | 1/8 | 1/8 | 1/8 | 0 | 高斯点 |
| g2 | 1/8 | 1/8 | 1/8 | 5/8 | 0 | 高斯点 |
| g3 | 1/6 | 0 | 0 | 2/3 | 1/6 | 高斯点 |
| g4 | 2/3 | 0 | 0 | 1/6 | 1/6 | 高斯点 |
与FEM以单元刚度矩阵组装总刚度矩阵不同, 本文ES-FEM以光滑域刚度矩阵组装总刚度矩阵。编程过程中发现, 与FEM相比ES-FEM延长了总刚度矩阵的半带宽。如图 1所示, FEM中结点3与结点5并无联系, 总刚度矩阵中的K35位置为零元素; 而ES-FEM中由于光滑域Ωms刚度矩阵k35非零, 故总刚度矩阵中K35也非零。
2 算例分析本文利用C++语言编程建立了悬臂梁模型和无限大带孔板模型。采用经典有限元三角形单元 (FEM-T3)、任意四边形单元 (FEM-Q4)、光滑子单元域四边形单元 (CSFEM-Q4)、光滑边域三角形单元 (ESFEM-T3) 分别对两种模型进行分析计算。为了便于比较各种方法的收敛性引入了位移误差范数ed和应变能误差范数ee, 定义如下:
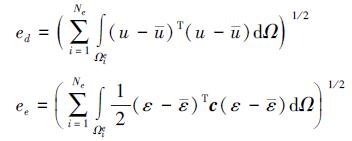
|
(13) |
式中,Ne表示单元总数, c表示材料的弹性矩阵。
S-FEM中, 单元内部应力/应变场在光滑域间不连续, 故采用围绕单元节点光滑域面积加权平均的方法重获应力/应变场。
2.1 悬臂梁模型如图 2所示, 长度为L、宽度为D的矩形悬臂梁一端固支另一端施加垂直向下的牵引力, 力的大小沿自由端呈半椭圆形变化。考虑平面应力状态, 故悬臂梁取单位厚度。

|
| 图 2 悬臂梁模型 |
其理论位移解与应力解为:
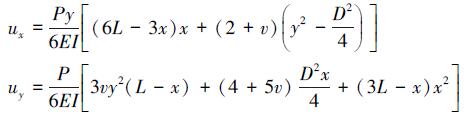
|
(14) |
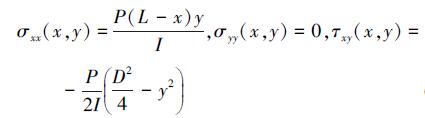
|
(15) |
式中, E为材料的弹性模量, v为泊松比, I为悬臂梁的惯性矩。
本文取长度L=48 m, 宽度D=12 m, 弹性模量E=3.0×107 N/m2, 泊松比v=0.3, 牵引力P=1 000 N, 并且分别采用三角形单元 (T3) 和任意四边形单元 (Q4) 划分问题域。本模型固支端的位移边界条件由公式 (14) 给定, 自由端的应力边界条件由公式 (15) 给定, 应变能的精确解可由理论推导出为4.474 6 Nm。
图 3给出了利用各种有限元法计算得到y=0处位移解的绝对误差。可以看出, FEM-T3的刚度矩阵偏“硬”, 位移解最小; 与之相比, ESFEM-T3与CSFEM-Q4的刚度矩阵比较“软”, 其位移解都与精确解非常吻合。CSFEM-Q4最为精确, ESFEM-T3与其非常接近。
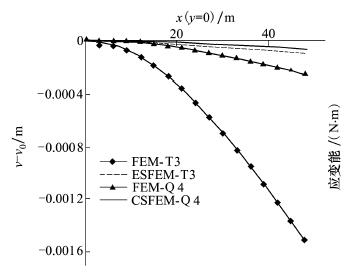
|
| 图 3 悬臂梁模型垂直方向位移误差对比 |
图 4展现了应变能随模型自由度数增加而逐渐收敛的趋势。可以看出, FEM-T3“偏硬”表现明显, 采用任意四边形单元的CSFEM-Q4最为精确, 而采用常应变三角形单元的ESFEM-T3与CSFEM-Q4的结果一样好。
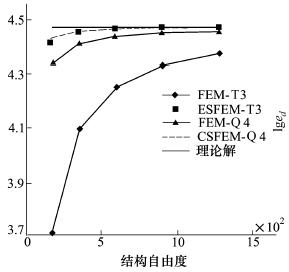
|
| 图 4 悬臂梁模型应变能收敛趋势图 |
图 5给出了位移误差范数随单元尺寸的收敛趋势。可以看出, 在网格划分方式相同的条件下, ESFEM-T3和CSFEM-Q4计算结果最为精确; 而当网格划分更为细密时 (lgh<0.3), ESFEM-T3计算结果最为精确。当h=1m (lgh=0) 时, ESFEM-T3的位移误差范数是FEM-T3的1/64、FEM-Q4的1/9、CSFEM-Q4的2/5。
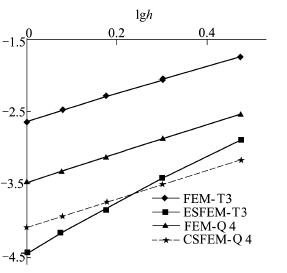
|
| 图 5 悬臂梁模型位移误差范数随单元尺寸收敛趋势图 |
图 6所示为应变能误差范数的收敛趋势 (后缀-Re表示应力修均后的结果)。可以看到FEM-Q4的重获应变场最为精确, ESFEM-T3的误差范数虽然比FEM-Q4-Re和CSFEM-Q4较大, 但远小于FEM-T3、FEM-T3-Re和FEM-Q4。
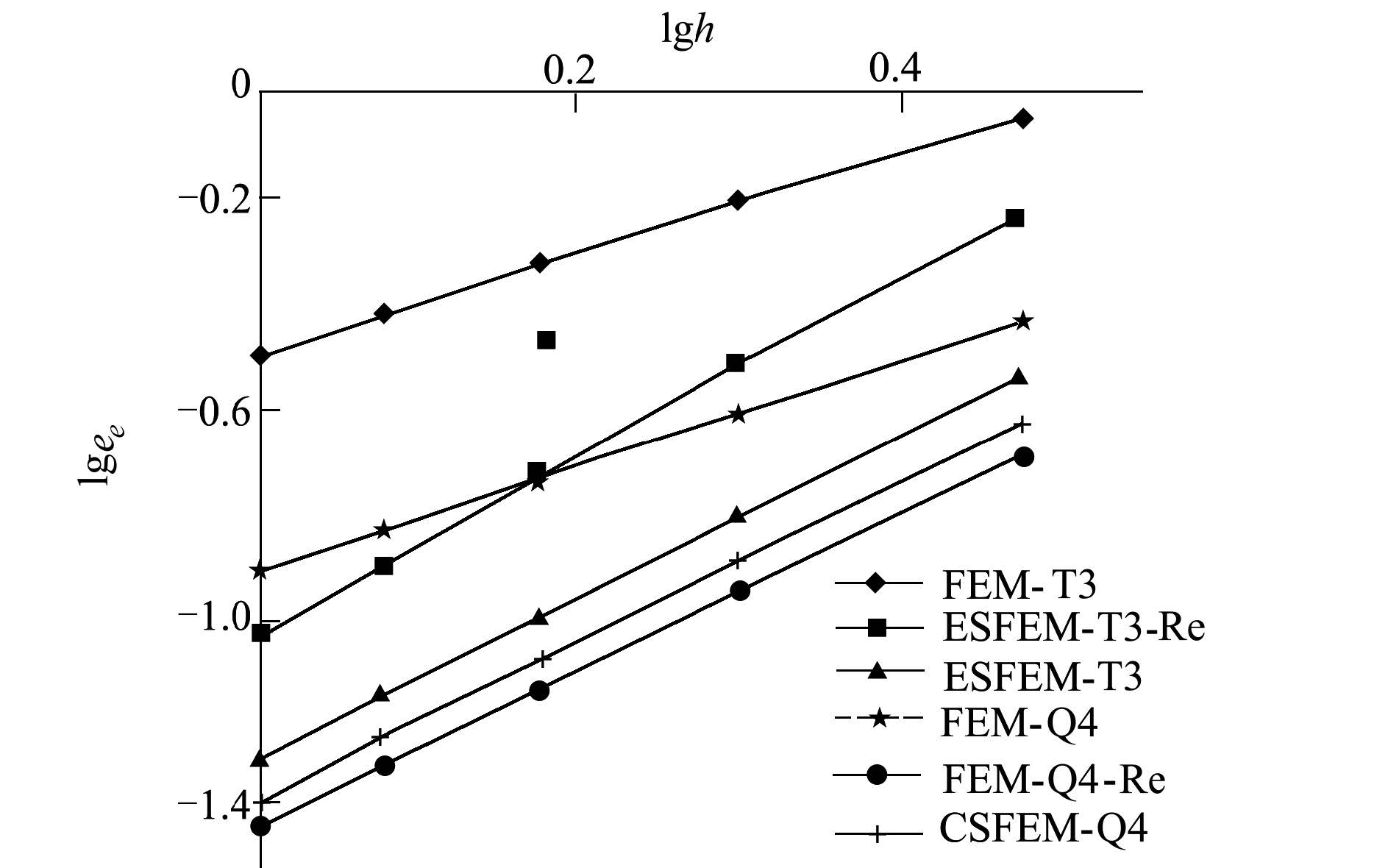
|
| 图 6 悬臂梁模型应变能误差范数随单元尺寸的收敛趋势图 |
图 7a) 所示无限大板中心带半径a=1 m的圆孔。其x方向无限远处受σ=1 N/m的拉应力。建模过程中考虑对称性, 取1/4模型, 边界条件如图 7b) 所示。分别采用三角形 (T3) 和任意四边形 (Q4) 单元划分网格。模型考虑平面应力状态, 取弹性模量E=1 000 N/m2, 泊松比v=0.3。
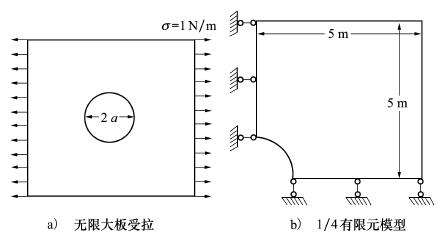
|
| 图 7 无限大带孔板模型示意图 |
由弹性力学可推出其理论位移解为:
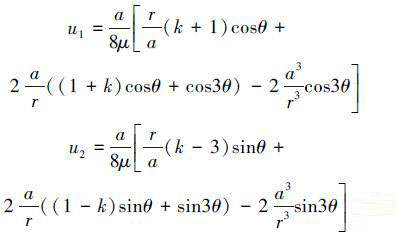
|
(16) |
式中,μ=E/(2(1+ν)), k可定义为平面应变状态下的泊松比:k=3-4ν。
模型的精确应力解为:
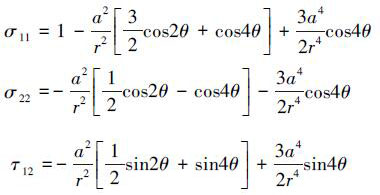
|
(17) |
式中,(r, θ) 是极坐标系参数, 坐标系原点在孔心处, θ=0°方向为x轴方向。
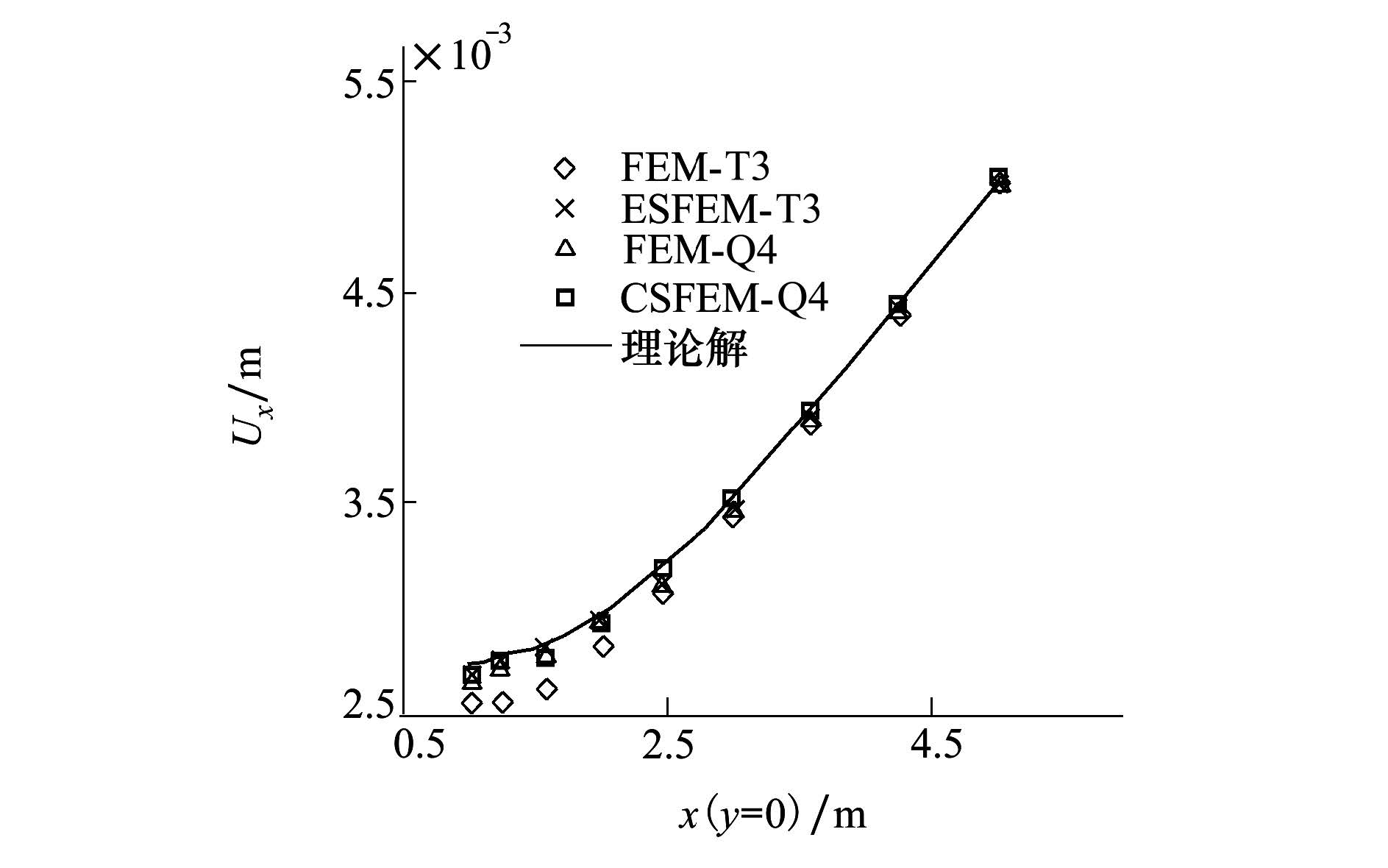
图 8为ESFEM-T3、FEM-T3、FEM-Q4和CSFEM-Q4的位移解与精确解的比较示意图。与悬臂梁模型相同, FEM-T3的刚度矩阵偏“硬”导致位移解偏小。而其他方法的位移解虽然也偏小但与精确解几乎重合。
|
| 图 8 模型底部X方向位移解示意图 |
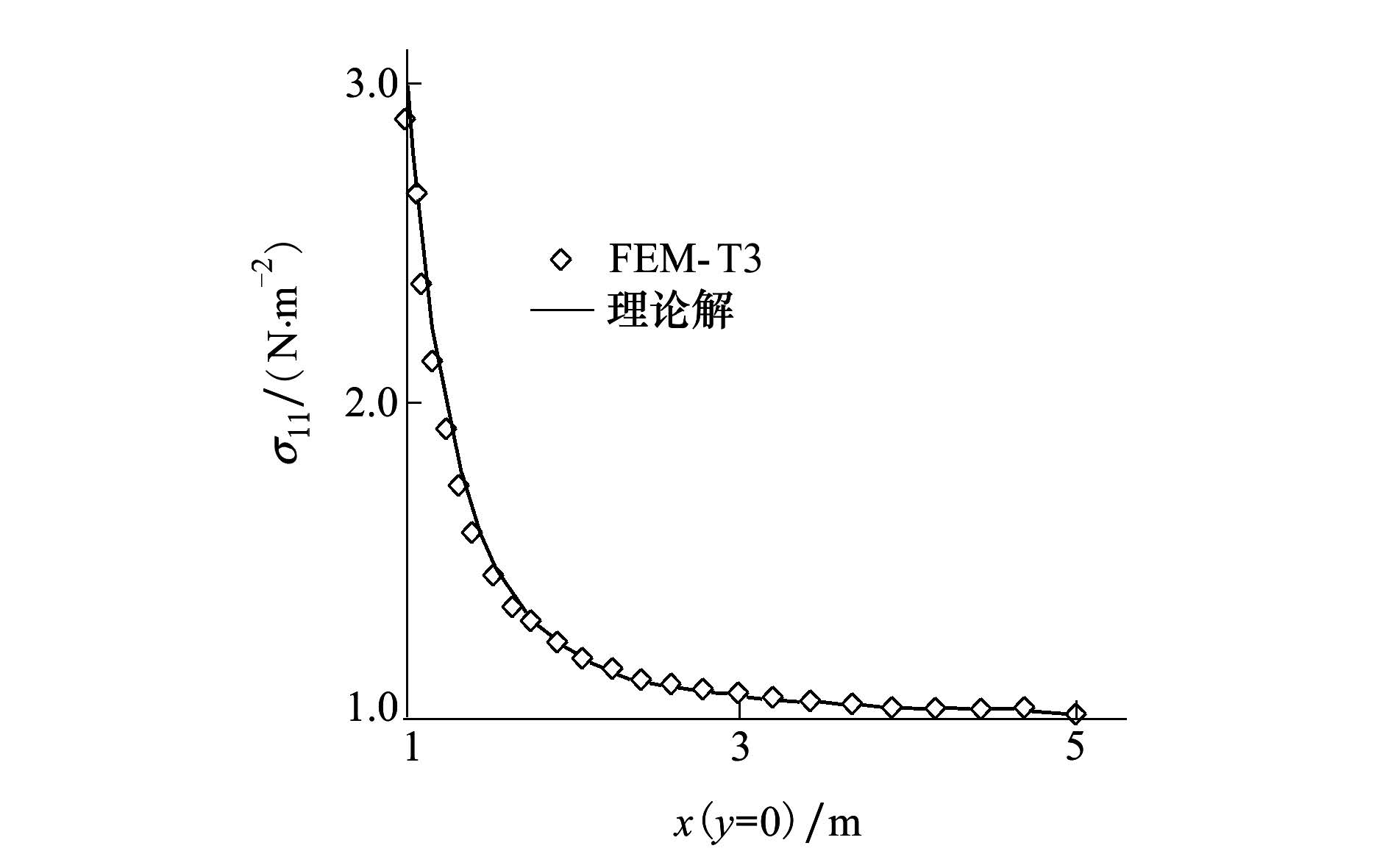
图 9给出了模型在x=0处的正应力解与理论解对比示意图。可以看出, ESFEM-T3的应力解与理论解非常吻合。图 10给出了应变能随单元结点数目的变化趋势。从图中可以看出, ESFEM-T3的收敛性最佳, 甚至优于CSFEM-Q4。
|
| 图 9 模型左边界X方向正应力解与理论解 |

|
| 图 10 限大带孔板模型应变能随自由度的收敛曲线 |
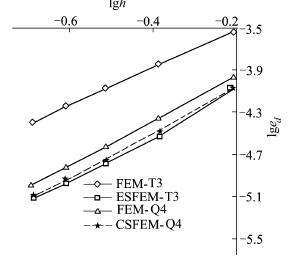
图 11给出了ESFEM-T3、FEM-T3、FEM-Q4和CSFEM-Q4的位移误差范数收敛趋势。可以明显看出ESFEM-T3的位移误差范数最小, 当采用最细密的网格时 (h=0.196 9 m), 其位移误差是FEM-T3的1/5, FEM-Q4的3/4并且略小于CSFEM-Q4。
|
| 图 11 位移误差范数随单元尺寸收敛趋势图 |
图 12给出了各种方法计算得到的应变能误差范数的收敛曲线。可以看出, ESFEM-T3收敛性明显优于FEM-T3、FEM-Q4和FEM-T3-Re, 与FEM-Q4-Re和CSFEM-Q4非常接近。
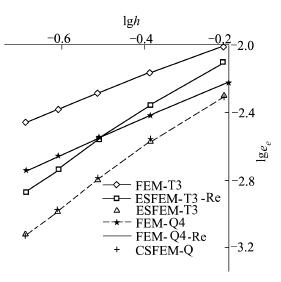
|
| 图 12 无限大带孔板模型应变能误差范数收敛趋势图 |
本文利用C++编程建立了悬臂梁和无限大带孔板模型, 分别采用FEM-T3、ESFEM-T3、FEM-Q4和CSFEM-Q4 4种有限元法进行计算, 并与精确解比较以探究ES-FEM在二维线弹性力学方面的应用特性。得出结论如下:
与经典有限元法相比, ES-FEM具有超高的收敛性和精确性。在结点分布相同的情况下, ESFEM-T3数值解的位移误差范数和应变能误差范数都远低于FEM-T3和FEM-T3-Re, 甚至低于FEM-Q4和FEM-Q4-Re。
| [1] | Liu G R, Nguyen T T. Smoothed Finite Element Methods[J]. Tsinghua Science & Technology, 2007, 12(5): 497–508. |
| [2] | Liu G R, Dai K Y, Nguyen T T. A Smoothed Finite Element Method for Mechanics Problems[J]. Comput Mesh, 2007, 39: 859–877. |
| [3] | Nguyen X H, Nguyen H V, Bordas S, et al. A Cell-Based Smoothed Finite Element Method for Three Dimensional Solid Structures[J]. KSCE Journal of Civil Engineering, 2014, 16(7): 1230–1242. |
| [4] | Liu G R, Zeng W, Nguyen X H. Generalized Stochastic Cell-Based Smoothed Finite Element Method (GS-CS-FEM) for Solid Mechanics[J]. Finite Elements in Analysis & Design, 2013, 63(1): 51–61. |
| [5] | Dai K Y, Liu G R, Nguyen T T. An N-Sided Polygonal Smoothed Finite Element Method (nSFEM) for Solid Mechanics[J]. Finite Elements in Analysis & Design, 2007, 43(11/12): 847–860. |
| [6] | Liu G R, Nguyen T T, Nguyen X H, et al. A Node-Based Smoothed Finite Element Method (NS-FEM) for Upper Bound Solutions to Solid Mechanics Problems[J]. Computers & Structures, 2009, 87(s1/2): 14–26. |
| [7] | Liu G R, Nguyen T T, Lam K Y. An Edge-Based Smoothed Finite Element Method (Es-FEM) for Static, Free and Forced Vibration Analyses of Solids[J]. Journal of Sound & Vibration, 2009, 320(4/5): 1100–1130. |
| [8] | Nguyen T T, Liu G R, Nguyen X H. An N-Sided Polygonal Edge-Based Smoothed Finite Element Method (nES-FEM) for Solid Mechanics[J]. International Journal for Numerical Methods in Biomedical Engineering, 2011, 27(9): 1446–1472. |
2. Science and Technology on Reliability and Environment Engineering Laboratory, Beijing Institute of Structure and Environment Engineering, Beijing 100076, China


