人字齿行星传动在结构上将人字齿轮和行星齿轮二者的优点有效结合,具有结构紧凑、承载力强等诸多优点,因而在航空航天、船舶重工、兵器装备等工业传动领域得到诸多应用,作为一种内、外啮合型传动受到了学者们的广泛关注[1-4]。Sondkar等建立了人字齿行星系统的动力学模型,并求解分析了其固有特性和均载稳定性[5-6]。赵永强等在弯扭耦合动力学模型基础上,重点研究了人字齿行星传动的自由振动模式[7]。齿轮工作中由于啮合传动的时变刚度、齿侧间隙等非线性因素相互影响,对其动载特性、传动噪声及均载稳定性均有较大影响,大量研究[8-10]表明轮齿啮合间的时变刚度通常是齿轮系统传动中振动不均和动载波动的重要因素。人字齿行星传动在结构上可视为2对斜齿行星齿轮的组合体,轮体两侧存在多处内、外啮合副的接触和脱离,加之齿轮副间多种非线性因素的激励,使得运动状况异常复杂,动力学分析时需考虑的自由度和啮合因素较多,导致后期求解和研究困难[11]。为探索其运动中的振动特性有必要做进一步的研究。
本文根据啮合理论详细推导了齿轮传动单齿啮合时变啮合刚度,在Poincaré映射思想和牛顿迭代法基础上研究了系统的稳态特性和非线性振动特性。
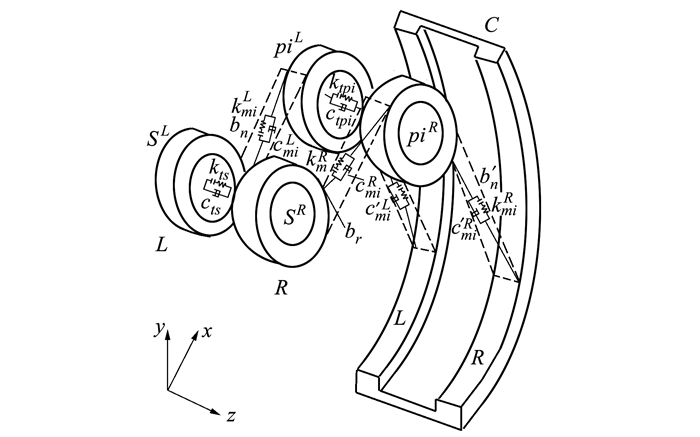
1 动力学模型建立图 1人字齿行星传动系统纯扭转动力学模型,o-xyz为系统全局坐标系, 坐标原点o位于太阳轮的几何中心, z轴沿构件轴向垂直截面向外, x轴沿构件的径向向外, y轴则根据右手定则确定, 人字齿左右侧啮合副之间视为欧拉梁单元衔接, 各行星轮具有相同的物理和几何参数。
|
| 图 1 人字齿行星齿轮啮合型扭转动力学模型 |
所建模型基于以下假设[12]:①系统中扭转运动关于几何中心o对称, 齿轮本体及行星架视为刚体且具有相同物理属性; ②内、外啮合副间由弹簧和阻尼相连, 不考虑齿面间滑动摩擦; ③啮合线位于啮合平面内, 阻尼力和啮合力视为啮合位移函数关系。假定外啮合时沿太阳轮指向行星轮方向为正方向, 内啮合时沿行星轮指向内齿圈方向为正方向。不考虑内齿圈的扭转振动, 根据质点系动量矩定理, 由集中质量法建立含间隙人字齿行星齿轮动力学方程如(1)式所示。
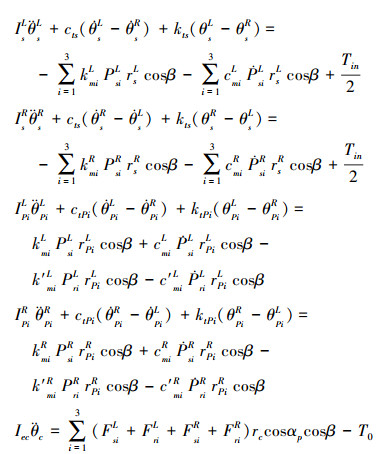
|
(1) |
式中, Tin为输入转矩, To负载转矩, L代表左侧啮合齿对, R表示右侧, Ij(j=s, Pi, ec)表示转动惯量, Iec=Ic+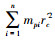
对于人字齿行星齿轮传动, 仅考虑构件间的扭转相对振动, 未考虑耦合作用, 则行星轮与太阳轮、内齿圈之间沿啮合线方向的啮合力FspiL、FspiR、FrpiL、FrpiR可分别表示为
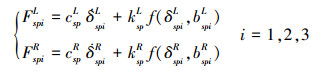
|
(2) |
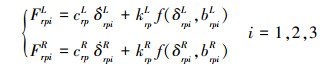
|
(3) |
式中, kspi, krpi (i=L, R)为啮合法线方向的时变啮合刚度。
齿轮运转过程中参与啮合的轮齿对数以及啮合线长度随着时间周期性变化, 为准确分析时变啮合刚度随啮合运动的关系, 现根据啮合传动原理[11], 求出任意瞬时轮齿啮合接触刚度。首先由齿轮设计手册求得平均啮合刚度km, 再计算一个周期T内的平均接触线长度lm, 得到刚度-接触线系数ξ=km/lm。根据啮合原理, 在啮合接触区域内, 不同时刻啮合齿总对数为N, 接触线总长l为时间t的函数, 啮合区域以匀速V=2πrb1n1从右向左平动, 其中, rb1为主动轮基圆半径, n1为主动轮转速, 则由总重合度ε知瞬时啮合齿对数N为
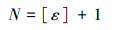
|
(4) |
而t时刻啮合区总接触线长度l(t)为
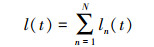
|
(5) |
从而可求得齿轮时变啮合刚度

|
(6) |
式中, k(t)为周期性时变值。
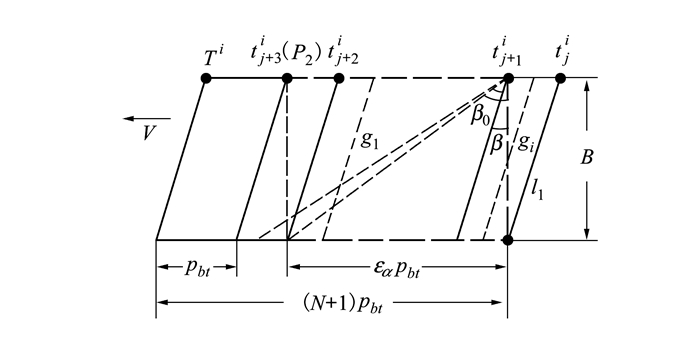
图 2所示为轮齿啮合运动示意图, 节圆啮合平面内, 虚线矩形表示齿轮啮合区域, P1, P2为轮齿进入和脱离啮合点, g1, gi为某时刻参与啮合的齿对, tji为临界啮合点, i表示螺旋角类型, j表示一个啮合周期内的临界时刻点, Ti为单齿啮合周期。由轮齿啮合传动关系知, 根据螺旋角β大小可将啮合接触运动分为3种情况:β < β0、β=β0和β>β0, 其中β0为临界螺旋角。
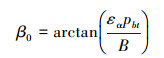
|
(7) |
式中, εα为端面重合度, pbt为端面节距, B为从动轮齿宽。
|
| 图 2 轮齿啮合运动示意图 |
对于β < β0,时变啮合刚度公式k(t)为
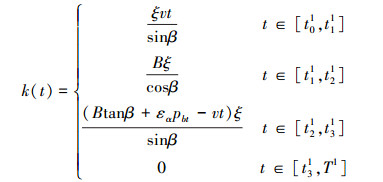
|
(8) |
啮合传动中的齿侧间隙是引起非线性振动的主要激励源, 为等效实际啮合情况, 令齿侧间隙为2bi, 取bi=10 μm, 内、外啮合的间隙非线性函数如下
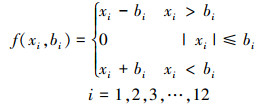
|
(9) |
在人字齿行星传动中, 行星轮与行星架之间视为刚性连接, 内、外啮合副啮合点处沿啮合法线方向产生的动态相对位移δspiL、δspiR、δrpiL、δrpiR分别为
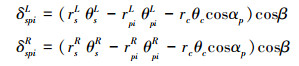
|
(10) |
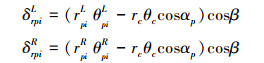
|
(11) |
式中, i=1, 2, 3。
由于行星轮、太阳轮和内齿圈在扭转方向存在刚体位移, 导致刚度矩阵产生奇异方程组(1)无法求解, 引入转动刚体间的相对位移x1、xpi分别为
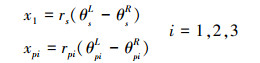
|
(12) |
将(12)式分别带入(1)式、(10)式和(11)式中消除刚体位移, 构建含新自由度的方程组, 鉴于人字齿行星齿轮尺寸和结构的对称性, 对消除系统刚体位移后的新方程组进行简化处理, 所用变量如下
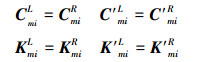
|
为避免方程中系数差值过大而产生病态问题, 对上述方程组进行量纲一化处理, 引入位移标称尺度bc=100×10-6m, 令无量纲时间τ=ωnt
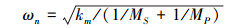
|
(13) |
可推导出如下量纲一化变量式[12-13]
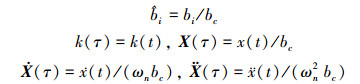
|
将上述变量代入消除刚体位移后的方程组, 进行量纲一化处理。对于含16自由度的间隙型非线性微分方程组, 整理后的系统动力学方程可统一表述为如下二阶微分方程式的形式
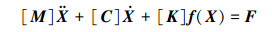
|
(14) |
式中
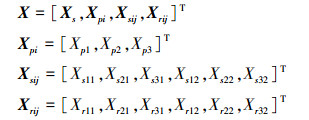
|
因系统整体动力学方程较为复杂, 仅将量纲一化后方程中的内、外啮合位移Xsij、Xrij的阻尼矩阵Csij、Crij和刚度矩阵Ksij、Krij列出, 如下所示
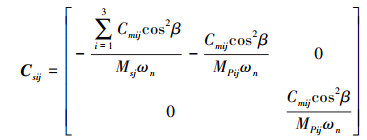
|
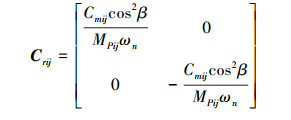
|
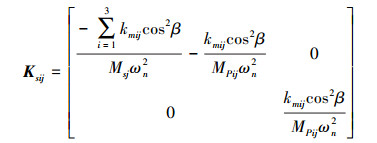
|
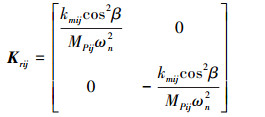
|
式中, i=1, 2, 3;j=1, 2。Msj为太阳轮与行星轮间的等效质量, MPij为内齿圈与行星轮间的等效质量。
2 非线性方程组求解为准确而高效地获得系统稳态解, 引入状态变量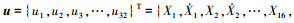
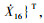
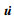
以{xi(t), 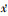
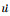
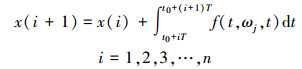
|
(15) |
则系统方程变为如下非线性方程的解曲线问题
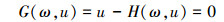
|
(16) |
当给定初始ω0, 根据常微分方程柯西问题知(18)式可转化为

|
(17) |
已知ωi时Poincaré截面上的映射序列ui={Xi, 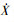
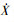
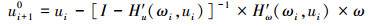
|
由牛顿迭代法可得修正后的ui+1为
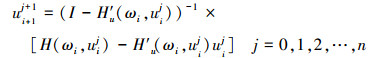
|
(18) |
通过状态变量, 对H′u (ωi, ui)、H′ω(ωi, ui)根据下面的微分方程组进行求解
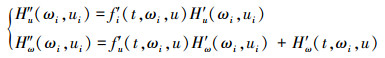
|
(19) |
式中, ωi为系统量纲一化后的频率, ui={Xi, 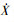
表 1为人字齿行星齿轮系统主要参数, 其中齿轮模数为4, 行星轮数目为3, 两侧螺旋角β为16°, 法面压力角α为20°, 输入转矩Tin=1 425 N·m, 啮合阻尼比系数μ=0.05, 扭转阻尼比系数为ζ=0.01。
| 项目 | 齿数z | 模数m/mm | 质量M/kg | 转动惯量I/(kg·m2) | 扭转刚度k/(N·m-1) |
| 太阳轮 | 23 | 4 | 1.021 | 0.001 4 | 2.59×107 |
| 行星轮 | 43 | 4 | 2.65 | 0.013 5 | 4.42×108 |
| 行星架 | — | — | 2.92 | 0.129 0 | 1.45×108 |
| 内齿圈 | 109 | 4 | 3.955 | 0.215 | — |
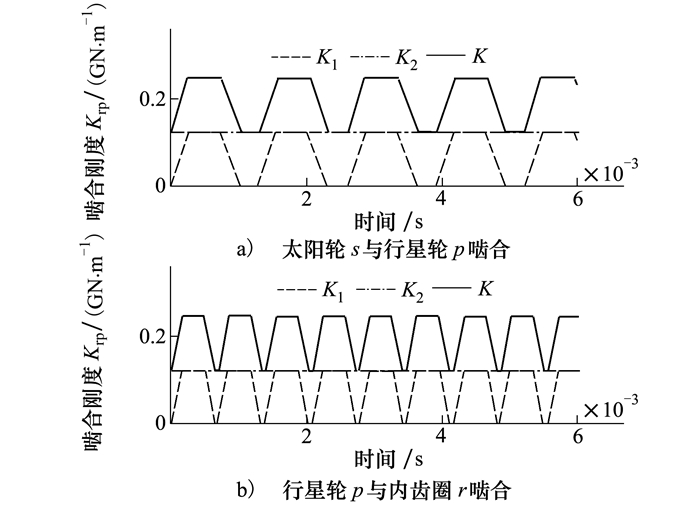
图 3所示为人字齿行星传动内、外啮合刚度时变图, 由图中所示总啮合刚度K由单齿啮合刚度K1和K2叠加而成。
|
| 图 3 人字齿行星传动内、外啮合时变刚度 |
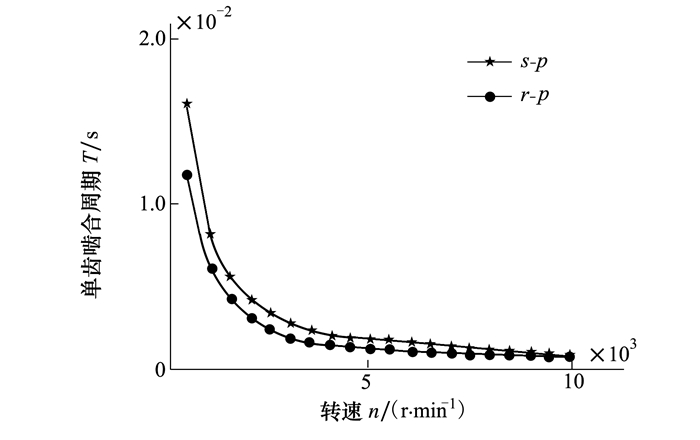
可以看出内、外啮合在传动过程中最多由2对轮齿相接触, 且每时刻均处于啮合状态, 未出现脱齿现象。内啮合传动刚度为0.28 GN/m大于外啮合时的0.25 GN/m, 二者均为周期性梯形波, 且刚度变化不具有同步性, 这是由于内、外啮合之间传动比不同以及啮合相位的差异, 使得二者具有不同的相对速度和周期。由图 4单齿啮合周期可以看出在转速增加过程中, 轮齿啮合周期不断降低, 在转速1 000 r/min附近周期变化较为剧烈, 当转速大于2 500 r/min后, 基本保持0.002 s的单齿啮合周期。
|
| 图 4 单齿啮合周期 |
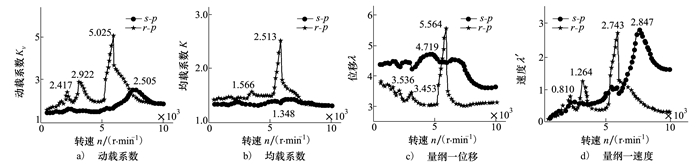
图 5a)和图 5b)中分别考虑了人字行星齿轮传动时内、外啮合的动载特性和均载特性, 外啮合在低速运转过程中较为稳定动载系数Kv为1.45, 当系统转速达到7 500 r/min时, 此时振动较为剧烈动载系数为2.505, 内啮合传动在工作过程中出现了3次较为明显的振动峰, 整个振动过程不断产生波动, 其最大峰值发生在5 900 r/min处, 对应动载系数为Kv=5.025。在图 5b)中由均载特性可以看出, 外啮合的均载特性较好, 在整个转速区间基本保持在K=1.348, 内啮合在5 900 r/min处均载系数出现跃迁, 达到最大值K=2.513, 通过二者的动载特性分析表明太阳轮、行星轮的啮合传动在稳态特性上较行星轮、内齿圈啮合的稳定性更好。图 5c)和图 5d)分别从振动位移和速度方面对内、外啮合进行了分析, 外啮合的振动位移较为平缓, 内啮合在传动中位移出现跳跃式增加, 最大无量纲值达到5.564, 当转速大于7 500 r/min时, 二者的相对位移不同程度的出现降低, 但在整个传动过程中并未出现齿背冲击的现象。由图 5d)可见随着转速的增加, 二者的振动均逐渐增强, 行星轮与内齿圈间啮合较太阳轮啮合更快地出现振动峰值,当二者的转速分别达到5 900 r/min和7 500 r/min以后,振动速度开始逐渐下降。工况设计中,应注意内、外啮合不同的振动峰值区间,从而避开剧烈的转速区。
|
| 图 5 不同转速下系统的内、外啮合传动振动特性 |
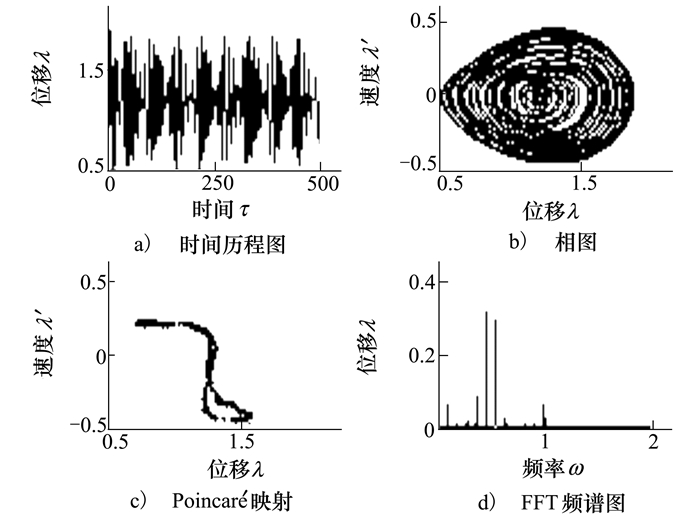
当太阳轮转速为12 000 r/min时, 啮合传动表现出拟周期振动, 如图 6所示。在位移响应中, 振动无量纲幅值为1.86且在一定范围内表现为谐波振动。其中相图中的轨迹在运动中不断扭曲缠绕但并不重合, 吸引子最终充满整个超环面形成分形结构, 运动过程中未出现齿背冲击。Poincaré截面为封闭扭曲状, 表明系统在振动过程中周期成分较多, 从而在一定范围内形成封闭环。由啮合位移FFT分析知, 振动中含有多种频率成分, 离散分布且相互独立, 频域分析与相图和Poincaré映射相吻合, 系统的拟周期振动并不同于混沌和周期运动。
|
| 图 6 拟周期振动 |
1) 根据齿轮啮合原理, 推导了轮齿啮合时变刚度公式, 计算了人字齿行星齿轮的内、外啮合刚度, 其时间历程均为周期性梯形波, 二者不具有同步性。
2) 人字齿行星传动中, 内啮合在多个转速区发生显著振动, 动载系数Kv最大值为5.025, 对应转速为5 900 r/min, 外啮合在整个速度区间较为稳定, 最大动载系数为2.505。当转速大于7 500 r/min时, 二者的啮合位移均出现下降, 但并未出现脱齿和齿背冲击现象, 人字齿行星齿轮的外啮合较内啮合具有更好的振动稳定性。
3) 逆周期响应时, 啮合传动的相轨迹扭曲严重在状态空间中形成封闭超环面, 吸引子不断层叠充满整个相空间, Poincaré映射形成封闭的环状, FFT频谱由一系列离散谱构成。
| [1] |
秦大同, 肖正明, 王建宏.
基于啮合相位分析的盾构机减速器多级行星齿轮传动动力学特性[J]. 机械工程学报 , 2011, 47 (23) : 20–29.
Qin Datong, Xiao Zhengming, Wang Jianhong. Dynamic Characteristics of Multi-Stage Planetary Gears of Shield Tunneling Machine Based on Planet Mesh Phasing Analysis[J]. Journal of Mechanical Engineering , 2011, 47 (23) : 20–29. DOI:10.3901/JME.2011.23.020 |
| [2] |
崔立, 宋晓光, 郑建荣.
考虑多间隙的齿轮柔性转子耦合系统非线性动力学分析[J]. 振动与冲击 , 2013, 32 (8) : 171–178.
Cui Li, Song Xiaoguang, Zheng Jianrong. Nonlinear Dynamic Analysis for a Geared Flexible Rotor System Considering Muliti-Clearance[J]. Journal of Vibration and Shock , 2013, 32 (8) : 171–178. |
| [3] | Eritenel T, Parker R G. Modal Properties of Three-Dimensional Helical Planetary Gears[J]. Journal of Sound and Vibration , 2009, 325 (1) : 397–420. |
| [4] | Ambarisha V K, Parker R G. Suppression of Planet Mode Response in Planetary Gear Dynamics through Mesh Phasing[J]. Journal of Vibration and Acoustics , 2006, 128 (2) : 133–142. DOI:10.1115/1.2171712 |
| [5] | Sondkar P, Kahraman A. A Dynamic Model of a Double-Helical Planetary Gear Set[J]. Mechanism and Machine Theory , 2013, 70 : 157–174. DOI:10.1016/j.mechmachtheory.2013.07.005 |
| [6] | Sondkar P. Dynamic Modeling of Double-Helical Planetary Gear Sets[D]. Columbus, The Ohio State University, 2012 http://wenku.baidu.com/view/41d358f4680203d8ce2f24b4.html |
| [7] |
赵永强, 李瑰贤, 常山, 等.
船用大功率两级人字齿行星传动系统的振动特性研究[J]. 船舶力学 , 2009, 13 (4) : 621–627.
Zhao Yongqiang, Li Guixian, Chang Shan, et al. Study on Vibration Characteristics of Two Stages Double Tooth Planetary Gear Trains Used in Ship with High Power[J]. Journal of Ship Mechanics , 2009, 13 (4) : 621–627. |
| [8] | Kwon H S, Kahraman A, Lee H K, et al. An Automated Design Search for Single and Double-Planet Planetary Gear Sets[J]. Journal of Mechanical Design , 2014, 136 : 1–13. |
| [9] |
郭家舜, 王三民, 刘海霞.
某新型直升机传动系统弯-扭耦合振动特性研究[J]. 振动与冲击 , 2009, 28 (10) : 132–140.
Guo Jiashun, Wang Sanmin, Liu Haixia. Lateral-Torsional Coupled Vibration Characteristics of Transmission of a New Type Helicopter[J]. Journal of Vibration and Shock , 2009, 28 (10) : 132–140. |
| [10] |
濮良贵, 纪名刚.
机械设计[M]. 8版. 北京: 高等教育出版社 ,2006 .
Pu Lianggui, Ji Minggang. Design of Machinery[M]. 8th Ed. Beijing: Higher Education Press , 2006 . |
| [11] | Bahk C J, Parker R G. Analytical Solution for the Nonlinear Dynamics of Planetary Gears[J]. Journal of Computational and Nonlinear Dynamics , 2011, 6 (2) : 1–15. |
| [12] | Lin J, Parker R G. Mesh Stiffness Variation Instabilities in Two-Stage Gear Systems[J]. Journal of Vibration and Acoustics , 2002, 124 (1) : 68–76. DOI:10.1115/1.1424889 |


