引用本文
马明生, 龚小权, 邓有奇, 赵辉. 一种适用于非结构网格的间断Galerkin有限元LU-SGS隐式方法[J]. 西北工业大学学报, 2016, 34(5): 754-760.
Ma Mingsheng, Gong Xiaoquan, Deng Youqi, Zhao Hui. An Implicit LU-SGS Scheme for the Discontinuous Galerkin Method on Unstructured Grids[J]. Journal of Northwestern Polytechnical University, 2016, 34(5): 754-760.
一种适用于非结构网格的间断Galerkin有限元LU-SGS隐式方法
马明生1,2, 龚小权1, 邓有奇1, 赵辉1     
1. 西北工业大学 航空学院, 陕西 西安 710072 ;
2. 中国空气动力研究与发展中心计算空气动力研究所, 四川 绵阳 621000
收稿日期: 2016-03-20
作者简介: 马明生(1962-), 西北工业大学兼职教授, 主要从事飞行器设计与计算流体力学研究。
摘要: 具有TVD性质的显式Runge-Kutta间断Galerkin（RKDG）格式在CFD领域得到广泛应用，但是显式计算稳定性差、计算效率低。为改善时间推进效率，基于高阶间断Galerkin有限元方法，采用欧拉一阶后差（BDF1），发展了一套高效的隐式LU-SGS（lower upper-symmetric Gauss-Seidel）求解方法，方法基于MPI并行实现，适合于不同计算精度。针对非线性系统左端项矩阵，对比了简化前后LU-SGS的计算效率。建立的间断Galerkin有限元方法基于非结构网格，采用Taylor基函数，计算精度最高达到四阶精度。通过NACA0012翼型以及M6机翼算例对发展的LU-SGS方法进行了考察，与显式算法相比，隐式格式的迭代步数和CPU时间均较大程度减小，效率能够提高1个量级以上。最后将隐式算法用于复杂外形翼身组合体F4的流场计算，结果表明所发展的隐式方法具有较好的鲁棒性，能够用于复杂外形计算。
关键词: 间断Galerkin有限元     欧拉方程     Taylor基函数     LU-SGS     计算效率     非结构网格    

随着CFD和计算机技术的发展, CFD工作者希望得到更精细的流场结构以及更准确的气动数据, 比如阻力、力矩、热流。精细化的网格或者高精度的计算格式是实现这些要求的途径之一。在规则网格上进行光滑函数的数值近似, n阶精度的计算格式, 计算误差与hn(h为网格尺寸)成正比。高精度格式能够给出一些复杂流动现象的精细流场结构, 相比传统二阶格式具有更高的分辨率。而非结构网格相比结构网格具有更大的灵活性, 更适应复杂外形和边界条件。因此发展适用于非结构网格的高精度格式一直是计算流体力学(CFD)研究的热点。

间断Galerkin有限元方法(discontinuous galerkin finite element method, DGM)是一种适合于结构网格以及非结构网格的高精度格式。它最早出现在1973年Reed和Hill[1]求解中子输运方程问题的论文中。DGM结合了有限体积法和有限元法的优点。作为一种有限元方法, 它采用有限元法中基函数思想来构造单元内的变量分布, 容易实现高精度。同时它又具有有限体积法积分形式的计算形式且融入了有限体积法中数值通量、Riemann间断、限制器等思想。DGM具有提高计算精度容易, 高精度时计算模板紧致, 适合非结构网格, 适合处理复杂外形及复杂边界、初值问题, 并行能力强, 自适应计算方便等优点。间断Galerkin有限元方法[2]在求解守恒方程组问题中得到广泛应用。经过Cockburn和Shu等的持续研究, 一种具有TVD性质的显式Runge-Kutta间断Galerkin(RKDG)格式得以逐步完善。

RKDG格式单步计算时间少, 内存需求量相对较小, 程序容易实现, 但是随着计算精度的提高, RKDG格式对应的稳定性条件将越来越严格, 时间推进步长受到明显限制, 计算效率低下, 特别是黏性计算。一些加速技术如当地时间步长、残值光顺、多重网格等, 在一定程度上加速了收敛过程。即便如此, 最大的时间步长依然受到当地稳定性条件的限制。与显式的时间格式相比, 隐式方法基本不受时间推进步长的限制, 因此发展高精度间断Galerkin有限元方法的时间隐式离散方法, 有着重要的工程应用价值。

目前间断Galerkin有限元方法已有多种高效的隐式离散方法, 比如带预处理的GMRES[3]、二阶的Crank-Nicholson(CN2)格式[4]、四阶隐式的Runge-Kutta(IRK4)等。LU-SGS隐式方法因为其在计算效率、鲁棒性及内存占用方面的优势, 在有限体积方法(FVM)中被大量采用。Yoon与Jameson在1988年[5]首先将其作为迭代方法用于方程求解, 随后Rieger和Jameson将其用于求解三维黏性流场, 从此各种改进的LU-SGS隐式方法被用来求解基于结构及非结构网格的流场。详细介绍LU-SGS在高精度间断Galerkin有限元方法中应用的文献较少, Haga和Wang将该方法用于基于非结构四面体网格的谱方法[6]。郝海兵、张强等在DGM四面体网格上实现了p=1阶的LU-SGS迭代[7]。郭永恒在其博士论文中[8]研究了不同LU-SGS改进方法对收敛的影响。刘伟在文献[9]中发展了基于Newton/Gauss-Seidel迭代的DGM隐式方法。

本文基于建立在非结构网格上的高精度间断Galerkin有限元方法, 发展了LU-SGS隐式计算方法, 比较了不同计算精度下的收敛曲线, 通过流场熵增云图给出了不同精度下的计算结果。同时对左端项进行了简化, 给出了左端项不同简化方法对收敛性的影响。给出了一系列二维、三维算例不同精度下的收敛曲线, 比较了二阶精度下有限体积和DGM下的收敛速度。

1 数值方法 1.1 控制方程

守恒形式的无黏可压缩欧拉方程组可写为

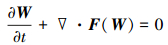
(1)

其中守恒变量、无黏对流通量为

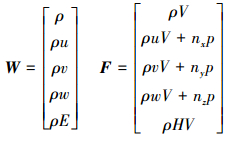
(2)

ρ、u、v、w、p、E、H分别代表密度、3个方向速度、压力、总能和总焓。

(3)

γ为比热比。

1.2 DGM空间离散

对方程组(1)采用间断Galerkin有限元离散。将其两端同时乘以测试函数φi, 并对整个求解域积分Ω, 再采用分部积分得到如下公式

(4)

式中，∂Ω为求解域Ω的边界, n为边界的法向量。将求解域Ω剖分为互不重叠的非结构网格单元, 并对每个单元采用上面的弱形式。每个计算单元的每个守恒变量在单元内的函数分布为

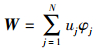
(5)

uj为单元守恒变量的自由度, 即为每时间步需要求解的量。N=N(p, d)由插值多项式阶数p和求解的空间维数d决定。φj是阶数为p的基函数。由于Taylor基函数[10]对所有单元形式都一样且为等级基, 对非结构混合网格较为合适, 因此本文采用Taylor基函数。将方程(5)带入方程(4)得

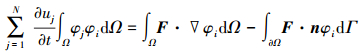
(6)

最后整个求解域方程可写为如下形式

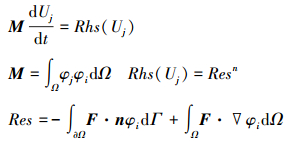
(7)

Res为无黏通量残差项, 由面积分和体积分构成, 二者均采用高斯数值积分计算。M为全局的质量矩阵, 由各单元的质量矩阵构成。无黏通量残差项具体计算为

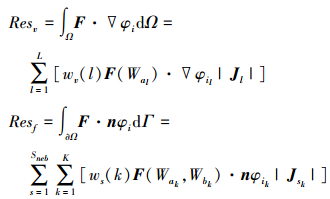
(8)

分别为体积分对应的单元高斯积分点的权系数、雅克比矩阵行列式值以及第i个基函数的梯度。ws(k)、|Jsk|、φis分别为单元面面积分对应的高斯积分点k的权系数、雅克比矩阵行列式值以及第i个基函数的值。Wak、Wbk分别对应边界面上当前单元和相邻单元在积分点k的变量值, Wal为当前单元体积分点l的变量值。

1.3 隐式LU-SGS方法

对方程(7)第一式采用一阶欧拉后差得到

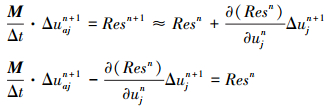
(9)

方程(9)为一大型的线性系统Ax=B, 其中矩阵A为一大型稀疏块矩阵。以三维p=3(四阶精度)DGM为例, 矩阵A的维数为n_cell×(5×20), n_cell为计算单元总数。如果直接存储该矩阵并求逆, 其存储量和计算量太大, 目前大多采用迭代法来求解该线性系统。

将面积分和体积分带入左端项的Resn。

(10)

将左端项矩阵写为

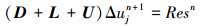
(11)

式中，D为对角块矩阵, L为严格下三角矩阵, U为严格上三角矩阵。

为方便推导, 进一步得到矩阵D、L、U, 本文只写出左端项矩阵中与当前计算单元有关的块, 将当前单元编号用a表示, 相邻单元用b表示,

对(10)式采用链式法则

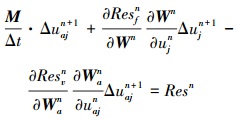
(12)

方程(11)左端项的面积分通量Resfn, 通过简单的LF数值通量格式计算

(13)

进一步得到面积分通量对守恒变量的偏导数

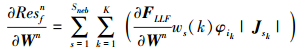
(14)

由方程(8)看到, 体积分通量为对流项与基函数梯度的点乘, 这里将基函数梯度类似看为面的法向量, 从而能够得到为变量对各自由度的偏导数即是多项式的基函数。

将方程(8)的第一项以及方程(14)带入方程(12)得

(15)

以三维p=3(四阶精度)DGM为例, 每个单元的左端项矩阵是大小为(5×20)×(5×20)的矩阵。令

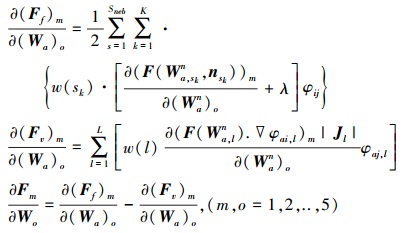
(16)

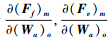
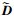
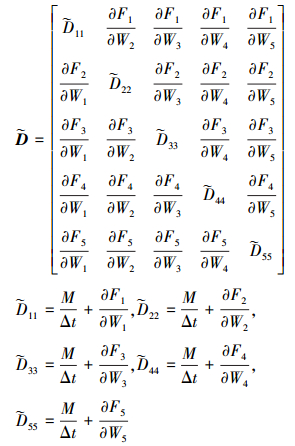
由于中都包含有基函数, 大小为N*N的矩阵, 的具体形式为

(17)

从方程(17)看到, 一般情况下矩阵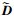几乎所有的元素不为零, 且不一定是主对角线占优, 这可能导致计算的稳定性降低, CFL数不能取大有限体积在求解左端项矩阵时大多对残差进行了降阶处理, 并且使用了无矩阵化技术来求(∂(Resn))/∂ujn)。由于DGM的残差包括体积分项和面积分项, 且通过高斯数值积分来求出, 计算费时, 针对欧拉方程组, 本文并没有采用无矩阵化技术, 而是直接采用解析方法求解。通过数值试验发现, DGM隐式方法的CFL数对左端项残差的处理比较敏感, 如果左端项残差近似处理不当, 可能导致CFL数只能取很小。针对左端项矩阵D, 如果求面积分(∂(Ff)m)/(∂(Wa)o)及体积分(∂(Fv)m)/(∂(Wa)o)时不采用各自的高斯积分点, 而只采用各自的边界面面心以及计算单元的体心, 会导致CFL只能取到小于2。本文采用Taylor基函数(体心展开), 左端项的体积分一项如果只采用体心来求, 导致(∂(Fv)m)/∂(Wa)o)出现很多零项, 可能改变了矩阵的性质, 导致CFL不能取大。

2 数值模拟结果及分析

本文首先通过等熵涡算例验证了DGM的计算精度。为验证本文发展的LU-SGS方法的收敛性, 计算了几类典型的测试算例。测试过程中, 右端对流通量项采用Roe′s格式, 并采用三阶TVD-Runge-Kutta方法来对比分析。利用NACA0012翼型亚声速算例考察了不同精度的LU-SGS收敛曲线, 研究了CFL数对收敛历程的影响, 给出了左端项简化前后的收敛曲线对比。计算了三维M6机翼亚声速绕流, 给出了不同精度的收敛曲线。最后通过F4翼身组合体给出了发展的LU-SGS隐式方法在复杂外形中的应用。在分析过程中, 本文采用成熟且经过验证的有限体积方法程序作为对比分析的参考。

2.1 等熵涡问题

等熵涡问题有精确解, 用来对二维Euler问题格式的精度进行验证, 这里把问题扩展到三维问题。等熵涡问题描述的是在初始的平均流(ρ, u, v, w, p)=(1, 1, 1, 0, 1)上加入一个等熵涡, 涡的大小按照(18)式给出。

(18)

式中，T=p/ρ, 熵S=p/ρr, ε为涡的强度ε=5.0;计算区域取为[0,10]×[0,10]×[0,10], 边界条件按照精确解给定, 时间上采用显式三阶Runge-Kutta法推进至2 s。计算采用的网格为N×N×N(N=10, 20, 40)六面体网格。表 1给出了不同精度下的L1 Error和L2 Error, 可以看到方法达到了设计的精度。

表 1 等熵涡问题精度验证(六面体网格)
精度网格L1误差阶数L2误差阶数
DG(p=1)10*10*103.03×10-38.52×10-3
20*20*206.36×10-42.2542.18×10-31.961
40*40*401.47×10-42.1075.17×10-42.080
DG(p=2)10*10*105.01×10-41.23×10-3
20*20*206.10×10-53.0371.54×10-43.000
40*40*408.33×10-62.8721.89×10-53.025
DG(p=3)10*10*102.01×10-45.13×10-4
20*20*209.99×10-64.3313.00×10-54.095
40*40*405.77×10-74.1121.80×10-64.058
表选项
2.2 NACA0012翼型亚声速绕流

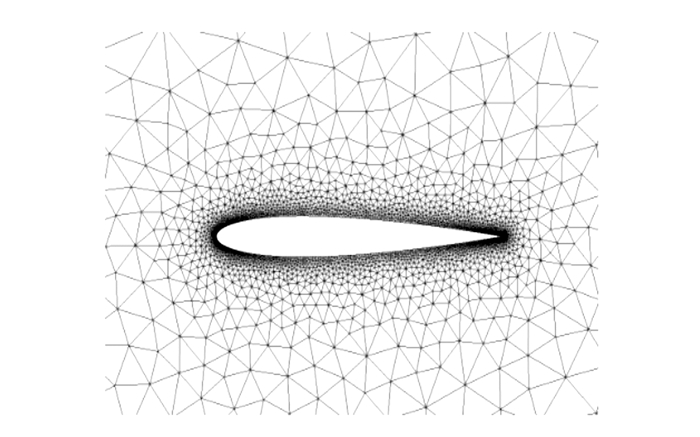
为考察DGM的精度以及发展的隐式算法的收敛性, 本文计算了NACA0012翼型在来流马赫数Ma=0.5时亚声速绕流。计算网格如图 1所示。

图 1 NACA0012计算网格
图选项

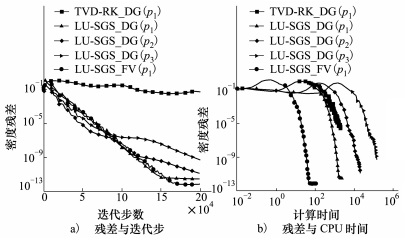
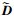
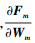
对称面共7 200个三角形单元, 通过展向拉伸对称面单元生成三棱柱单元。计算采用48个CPU并行, 给出了2～4阶DGM结果, 并与二阶的FVM进行了对比, 图 2给出了二阶RKDG、不同精度隐式DGM以及二阶FVM的残差收敛曲线, 此时显式的CFL=0.3, 隐式计算的CFL=10。从图看到, 相同二阶精度下, FVM和DGM残差收敛速度相当, 隐式收敛效率远高于显式。显示了二阶精度下, 不同CFL数的收敛曲线。从图看到, CFL数大于10后, 收敛速度基本不变, 从的构成看到, 的对角块矩阵包含两部分, 当CFL大于某个值后, 起相对主导的作用, 导致CFL数对收敛影响较小。

图 2 DGM不同计算精度及二阶FVM收敛历程
图选项

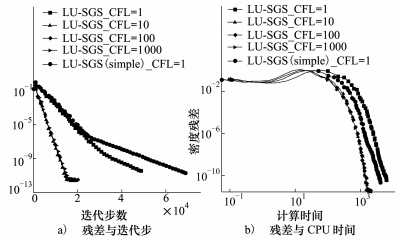
从图 3a)的曲线1和5, CFL=1, 简化左端项矩阵对收敛速度有一定影响, 导致迭代步数略有增加。从图 3b)看到, 对于CFL=1的情况, 由于简化左端项矩阵后, 单步计算时间减小, 总的收敛时间减小。由于简化左端项矩阵后CFL数不能取大, 因此未简化左端项矩阵当CFL数取大时, 其收敛速度快于简化后的状态。

图 3 DGM二阶精度不同CFL数收敛历程
图选项
2.3 ONERA M6机翼亚声速绕流

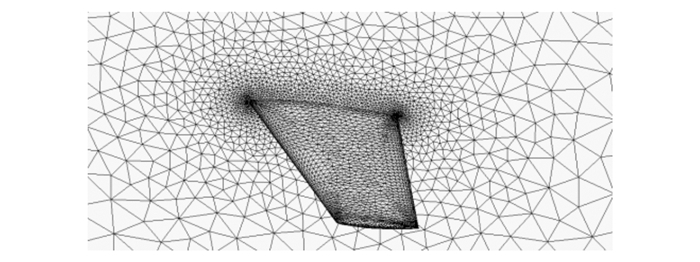
为进一步考察LU-SGS方法在三维外形计算效率, 本文计算了ONERA-M6亚声速流场, 计算马赫数Ma=0.5, 迎角0°。网格如图 4所示, 网格共约14万个四面体单元, 机翼前后缘及空间分别采用各向异性和各向同性四面体网格。计算采用64个CPU。

图 4 M6机翼计算网格
图选项

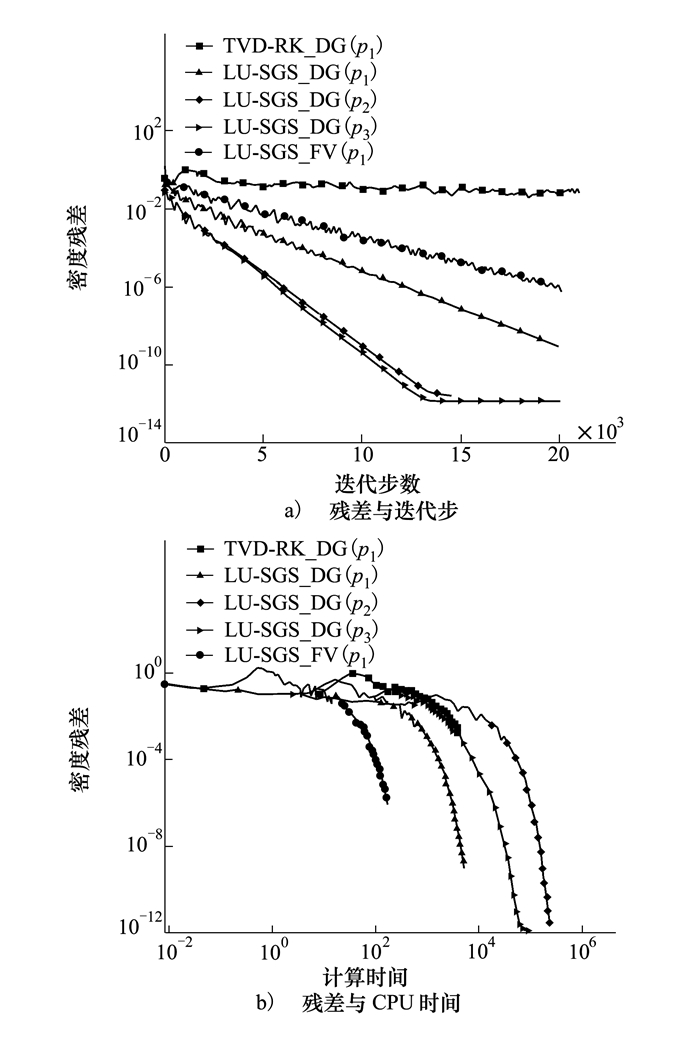
图 5给出了DGM不同计算精度下LU-SGS残差收敛曲线, 同时给出了FVM以及RKDG显式结果。隐式计算的CFL=1 000, 显式计算的CFL=0.3。从残差随迭代步数图看, 发展的LU-SGS隐式方法收敛效率远高于显式方法。二阶精度下, 由于DGM计算的自由度为FVM的4倍且计算面通量和体积分通量时采用更多的高斯积分点, 二阶DGM的单步计算时间远大于FVM。

图 5 不同计算精度DGM及二阶FVM收敛曲线
图选项
2.4 DLR-F4翼身组合体亚声速绕流

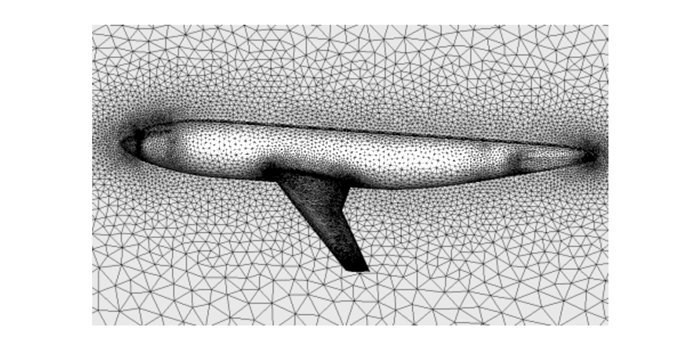
为验证发展的隐式算法的初步工程计算能力, 数值模拟了DLR-F4翼身组合体亚声速绕流。计算网格如图 6所示。

图 6 F4表面网格
图选项

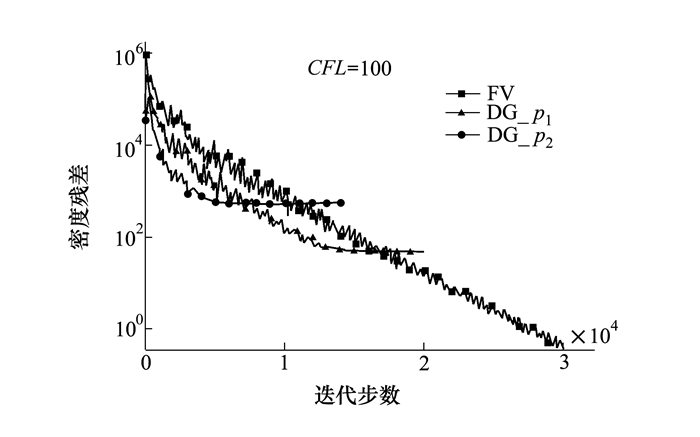
四面体网格单元总数为637 126个, 计算马赫数Ma=0.5, 来流迎角为0°, 计算采用128个CPU, 图 7给出了残差收敛曲线, 相同CFL数以及相同的dt计算方法下, 相对于有线体积方法, DGM残差收敛速度较快, 但是下降量级较少。这是由于在迭代过程中DGM一直修改迭代得到的自由度, 造成限制单元残差不降, 因此需要进一步研究该方法的限制器。

图 7 不同方法及精度的残差收敛曲线
图选项
3 结论

本文发展了一种高效的LU-SGS隐式计算方法, 方法适用于不同计算精度, 通过一系列的算例表明:

1) 本文发展的隐式方法CFL数能够取很大。相比显式RKDG, 其计算效率提高了1～2个量级。

2) 发展的隐式算法对左端项残差比较敏感, 需小心简化左端项残差, 简化可能限制CFL数, 导致整个计算时间增加, 计算效率降低。

3) 隐式计算时, 单元左端项矩阵包含时间项、面积分项和体积分项, 单元对应的矩阵D的矩阵元素几乎都不为零, 降低了CFL数对收敛性的影响。

4) 发展的隐式方法能够初步应用于复杂外形计算。

参考文献
[1] Reed W H, Hill T R. Triangular Mesh Methods for the Neu-Tron Transport Equation[R]. Technical Report LA-UR-73-479, Los Alamos Scientific Lab, 1973
[2] Cockburn B, Shu Chiwang. TVB Runge-Kutta Local Projection Discontinuous Galerkin Finite Element Method for Conservation Laws Ⅳ:The Multidimensional Case[J]. Mathematics of Computation , 1990, 54 : 545–581.
[3] Persson Per-Olof, Peraire Jaime. An Efficient Low Memory Implicit DG Algorithm for Time Dependent Problems[C]//44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 2006:9-12
[4] Wang L, Mavriplis D J. Implicit Solution of the Unsteady Euler Equation for High-Order Accurate Discontinuous Galerkin Discretizations[J]. J Comput Phys , 2007, 225 : 1994–2005. DOI:10.1016/j.jcp.2007.03.002
[5] Yoon S, Jameson A. Lower-Upper Implicit Schemes with Multiple Grids for the Euler Equatins[R]. AIAA-1986-0105
[6] Hagal Takanori, Sawada Keisuke, Wang Z J. An Implicit LU-SGS Scheme for the Spectral Volume Method on Unstructured Tetrahedral Grids[J]. Commun Comput Phys , 2009, 6 (5) : 978–996. DOI:10.4208/cicp
[7] 郝海兵, 张强, 杨永. 基于LU-SGS迭代的DGM隐式算法研究[J]. 西北工业大学学报 , 2014, 32 (3) : 346–350.
Hao Haibing, Zhang Qiang, Yang Yong. An Implicit Scheme of Discontinuous Galerkin Method(DGM) Based on LU-SGS Iterative Method[J]. Journal of Northwestern Polytechnical University , 2014, 32 (3) : 346–350.
[8] 郭永恒.双曲守恒律方程组的间断Galerkin方法研究[D].西安:西北工业大学, 2013
Guo Yongheng. Research of Discontinuous Galerkin Method for Hyperbolic Conservation Equations[D]. Xi'an, Northwestern Polytechnical University, 2013(in Chinese)
[9] 刘伟, 张来平, 赫新, 等. 基于Newton/Gauss-Seidel迭代的DGM隐式方法[J]. 力学学报 , 2012, 44 (4) : 792–796.
Liu Wei, Zhang Laiping, He Xin, et al. An Implicit Algorithm for Discontinuous Galerkin Method Based on Newton/Gauss-Seidel Iterations[J]. Acta Mechanica Sinica , 2012, 44 (4) : 792–796.
[10] Hong L, Baum J D, Lohner R. A Discountinuous Galerkin Method Based on a Taylor Basis for The Compressible Flows on Arbitrary Grids[J]. J Comput Phys , 2008, 227 : 8875–8893. DOI:10.1016/j.jcp.2008.06.035
An Implicit LU-SGS Scheme for the Discontinuous Galerkin Method on Unstructured Grids
Ma Mingsheng1,2, Gong Xiaoquan1, Deng Youqi1, Zhao Hui1     
1. School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China ;
2. China Aerodynamics Research and Development Center, Mianyang 621000, China
Abstract: The TVD explicit Runge-Kutta discontinuous Galerkin(TVD-RKDG) are widely used in CFD, but it has poor stability property and low computational efficiency. To improve the time advancing efficiency, an efficient implicit lower-upper symmetric Gauss-Seidel (LU-SGS) scheme based on backwards differencing methods (BDF1) has been applied to the high-order discontinuous Galerkin method. The method is implemented parallelly through MPI library and is suit for different computational orders. The left matrix of nonlinear system is simplified and computational efficiency is compared. The DGM is based on the Taylor basis functions on unstructured grid and the accuracy is up to forth order. The developed LU-SGS scheme is verified through NACA0012 airfoil and ONERA M6 wing. Compared to the traditional explicit Runge-Kutta scheme, the implicit scheme can greatly reduce the iteration number and CPU time. The computational efficiency can be accelerated evidently with more than one order of magnitude speed. At last the flow field of DLR-F4 is simulated to verify the robustness of the developed implicit scheme. The result proves that the developed LU-SGS scheme can be applied to complex configuration simulation.
Key words: discontinuous Galerkin method     Euler equations     Taylor basis     LU-SGS     computational efficiency     unstructured grid    
西北工业大学主办。
0

文章信息

马明生, 龚小权, 邓有奇, 赵辉
Ma Mingsheng, Gong Xiaoquan, Deng Youqi, Zhao Hui
一种适用于非结构网格的间断Galerkin有限元LU-SGS隐式方法
An Implicit LU-SGS Scheme for the Discontinuous Galerkin Method on Unstructured Grids
西北工业大学学报, 2016, 34(5): 754-760.
Journal of Northwestern Polytechnical University, 2016, 34(5): 754-760.

文章历史

收稿日期: 2016-03-20

相关文章

工作空间