体表胃电信号(EGG)是研究胃动力学特性和功能性胃疾病诊断的重要依据。胃电是一种典型的有用信号和噪声相选加的复合信号，其检测过程中会引入大量的强背景噪声。在实际应用中，由于胃电的检测过程中存在着很多不确定性，这些先验知识往往难以获得，因此胃电的检测与分析更类似一个在不确定的环境中提取与分析未知信号的过程。近年来，基于粗糙集、Vague集、软集等不确定理论发展起来的各类融合模型为解决胃电信号数据分析等问题研究提供了强有力工具和参考模型。
实践证明，任何单一的理论和方法都很难独自解决所有问题，甚至很难全面反映和处理某一个具体问题，因此研究各种不确定模型的扩展理论及其应用问题十分必要。粗糙集[1]理论基于集合中对象间的不可分辨性，在分析处理不确定信息时无须任何先验信息，其分析方法是相对客观的。基于覆盖关系建立的覆盖粗糙集模型是对经典粗糙集模型的扩展，由于其较好的应用前景得到了研究者的广泛关注[2, 3, 4, 5, 6, 7]。Vague集[8]理论作为模糊集的推广，在处理不确定性信息时比传统的模糊集有更强的表达能力及灵活性，是一种新型的处理模糊性问题的数学分析工具，有许多学者将其和其他处理不确定性信息模型结合开展研究。软集理论[9]是Moldtsov在1999年提出的一种新的处理不确定性和不精确性信息的数学工具，该理论克服了Vague集只能处理一部分不确定性信息的不足，目前在文本分类、数据挖掘、模糊决策、图像检索等领域成功应用。上述3种理论都关注信息系统中知识的不准确、不完备、不精准问题，在实际应用时既相互联系又相互补充，因此可以进行融合，以发挥各自的优势，弥补各自的不足。
因此，在研究Vague集和其他软计算理论的结合以及不确定性度量和相关应用背景问题方面，仍有大量的工作要做。针对Vague集、粗糙集和软集的结合问题，如文献[10]首次将粗糙集与软集思想进行融合，提出了粗糙软集的概念。文献[11]则将Fuzzy集与软集思想进行融合，提出了Fuzzy软集的概念。文献[12]将Vague集与软集思想进行融合，提出了新的Vague软集的基本概念并研究了相关性质、相似度量和不确定性度量等问题，但是没有研究Vague软集的相关应用问题。分析发现，类比覆盖粗糙Vague集模型，可以进一步在覆盖近似空间下将Vague软集和粗糙集进行融合，分别基于全邻域(∪Md(x))和近邻域(∩Md(x))定义2种新的覆盖粗糙Vague软集数学模型,并研究其相关性质,这是对覆盖粗糙集、Vague集和软集等理论的进一步扩展。同时,探讨Vague软集的相关应用问题也是一个重要的研究方向。另外,求属性重要性、属性核和属性约简是模糊数学理论中的几个主要问题,而不确定性度量作为各种软计算理论模型的一个重要数学特征,是上述问题的关键。
本文在上述研究的基础上,进一步在覆盖近似空间下将粗糙集、Vague集和软集3种不确定性理论方法进行融合,提出了一种全新的处理不确定信息的数学模型——覆盖粗糙Vague软集,并研究了相关性质及其不确定性度量方法,为下一步将该数学模型及其不确定性度量方法应用于胃电信号数据预处理问题奠定了相关理论基础。
1 预备知识下面对有关基础理论进行描述。
1.1 粗糙集定义1 (集合的下近似和上近似) 给定知识库(近似空间)K=(U,S),其中U为论域,S表示论域U上的等价关系簇,则∀X⊆U和论域U上的一个等价关系R∈IND(K),定义子集(概念或信息粒)X关于知识R的下近似和上近似分别为
|
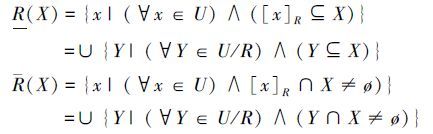
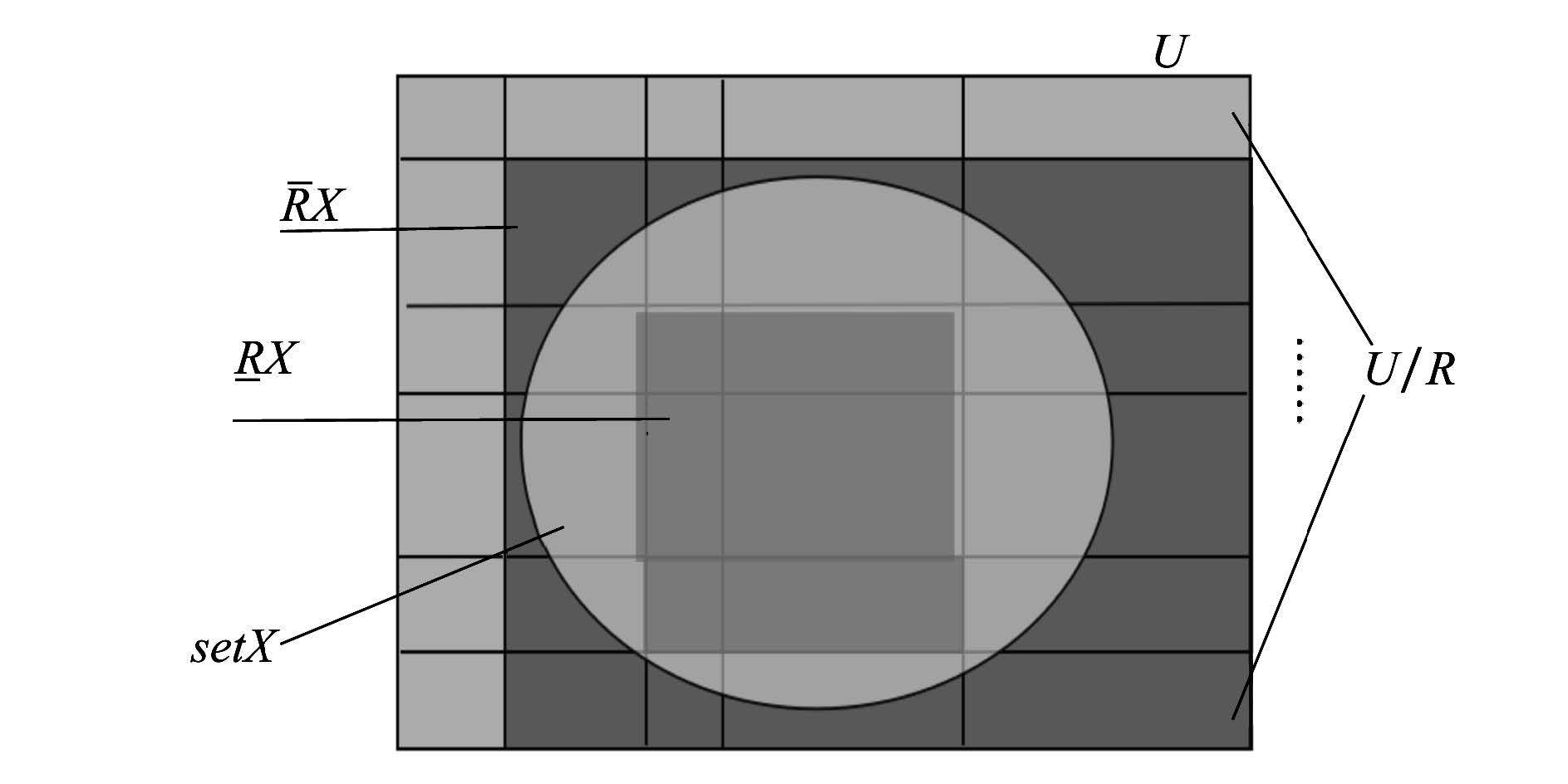
| 图 1 集合X的上近似、下近似和边界域 |
定义2(粗糙集) 给定论域U和其上的一个等价关系R,∀X⊆U,若R(X)=${\bar{R}}$(X),称集合X是关于论域U的相对于知识R的R-精确集或R-可定义集;若R(X)≠${\bar{R}}$(X),则称集合X是关于论域U的相对于知识R的R-粗糙集或R-不可定义集。
1.2 Vague软集文献[13, 14, 15]提出的Vague软集模型描述如下:
定义3(Vague软集) 设U是一个论域,E是一个参数集,A⊆E,且F:A→P(U)是一个映射,即∀e∈A,F(e)为U上的一个Vague集,称(F,A)为U上的一个Vague软集。
定义4(Vague软相等) (F,A)、(G,B)为U上的2个Vague软集,若A⊆B,且对于∀e∈A,x∈U,有tF(e)(x)≤tG(e)(x),fF(e)(x)≥fG(e)(x),则称(F,A)软包含于(G,B)(或称(G,B)软包含(F,A)),记作(F,A)${\tilde{\subseteq }}$(或(G,B)${\tilde{\supseteq }}$(F,A));若有(F,A)${\tilde{\subseteq }}$且(G,B)${\tilde{\supseteq }}$(F,A),则称(F,A)与(G,B)Vague软相等。
定义5(Vague软集的补集) 设(F,A)为U上的一个Vague软集,称(F,A)c=(Fc,⌉A)为(F,A)的补,其中Fc:⌉A→V(U),具体为∀⌉e∈⌉A,x∈U,有tFc(⌉e)(x)=fF(e)(x),1-fFc(⌉e)(x)=1-tF(e)(x)。
定义6(相对空的Vague软集) 设U是一个论域,E是一个参数集,A⊆E,(F,A)为U上的一个Vague软集,若∀e∈A,x∈U,tF(e)(x)=0,1-fF(e)(x)=0,则称(F,A)为U上的一个相对空的(相对于参数集A)Vague软集,记为φA。
定义7(相对全的Vague软集) 设U是一个论域,E是一个参数集,A⊆E,(F,A)为U上的一个Vague软集,若∀e∈A,x∈U,tF(e)(x)=1,1-fF(e)(x)=1,则称(F,A)为U上的一个相对全的(相对于参数集A)Vague软集,记为μA。
1.3 覆盖粗糙Vague集文献[16, 17]提出的覆盖粗糙Vague集模型描述如下:
定义8 (覆盖粗糙Vague集) 设(U,C)为覆盖近似空间,其中U为非空有限论域,C为U上的一个覆盖,对∀x∈U,Vague集关于覆盖近似空间(U,C)的上下近似分别为${\bar{C}}$(A),C(A),且有
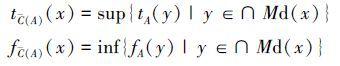
则称序对CV=(C(A),${\bar{C}}$(A))为基于覆盖的粗糙Vague集,简记为(CF(A),$\overline{CF}$(A))。其中,Md(x)=｛K∈C|x∈K∧(∀S∈C∧x∈S∧S⊆K⇒K=S)｝为x的最小描述。∩{K|K∈Md(x)｝称为x 的近邻域,记为CN(x)。
如同经典粗糙集的定义一样,在上述定义中,若对∀x∈U,有CF(A)(x)=$\overline{CF}$(A)(x),则称Vague集A关于覆盖近似空间(U,C)是可定义的,否则称Vague集A关于覆盖近似空间(U,C)是粗糙的。CF,$\overline{CF}$为基于覆盖的粗糙Vague集下近似算子和上近似算子。并规定基于覆盖的粗糙Vague集CV=ø,当且仅当CF(A)=ø且$\overline{CF}$(A)=ø。上述定义表明,任何Vague集模型在覆盖近似空间中,都可以用2个Vague集来逼近,即上近似$\overline{CF}$(A)和下近似CF(A)。
2 新的覆盖粗糙Vague软集本文在现有覆盖粗糙Vague集和Vague软集研究的基础上,进一步将2种模型融合,定义了一种新的覆盖粗糙Vague软集模型。
2.1 覆盖粗糙Vague软集的定义定义9 (覆盖粗糙Vague软集) 设(U,C)为覆盖近似空间,其中U为非空有限论域,C为U上的一个覆盖,(F,A)为U上的一个Vague软集。则Vague软集(F,A)关于覆盖近似空间(U,C)的上下近似分别为${\bar{C}}$(F,A),C(F,A),且有
则称序对CVS=(C(F,A),${\bar{C}}$(F,A))为覆盖粗糙Vague软集,记为(CVS(F,A),$\overline{CVS}$(F,A))。
在上述定义中,若对∀x∈U,有CVS(F,A)(x)=$\overline{CVS}$(F,A)(x),则称Vague软集(F,A)关于覆盖近似空间(U,C)是可定义的,否则称Vague软集(F,A)关于覆盖近似空间(U,C)是粗糙的。CVS(F,A)和$\overline{CVS}$(F,A)为基于覆盖的粗糙Vague软集下近似算子和上近似算子。并规定基于覆盖的粗糙Vague软集CVS(F,A)=φA,当且仅当CVS(F,A)=φA且$\overline{CVS}$(F,A)=φA。上述定义表明,任何Vague软集模型在覆盖近似空间中,都可以用2个Vague软集来逼近,即上近似$\overline{CVS}$(F,A)和下近似CVS((F,A))。
从定义9可以看出,在覆盖空间(U,C)上定义的粗糙Vague软集,表示的是在覆盖知识C上用论域上一对可定义的下近似和上近似子集来逼近所讨论的模糊对象集合,从而可以发现模糊信息系统中一些隐藏的知识。
2.2 覆盖粗糙Vague软集的性质下面讨论覆盖粗糙Vague软集的一些重要性质。
性质1 设(U,C)为一覆盖近似空间,(F,A)和(G,B)分别为论域U上的2个Vague软集,则覆盖粗糙Vague软集下近似算子CVS和上近似算子$\overline{CVS}$具有如下性质:
1) CVS(φA)=$\overline{CVS}$(φA)=φA,CVS(μA)=$\overline{CVS}$(μA)=μA;
2) CVS(F,A)${\tilde{\subseteq }}$(F,A)${\tilde{\subseteq }}$$\overline{CVS}$(F,A);
3) 可加性1:CVS((F,A)∩(G,B))=CVS((F,A))∩CVS((G,B));
4) 可加性2:$\overline{CVS}$((F,A)∪(G,B))=$\overline{CVS}$((F,A))∪$\overline{CVS}$((G,B));
5) 单调性:(F,A)${\tilde{\subseteq }}$⇒CVS(F,A)${\tilde{\subseteq }}$CVS(G,B),$\overline{CVS}$(F,A)${\tilde{\subseteq }}$$\overline{CVS}$(G,B);
6) CVS((F,A)c)=($\overline{CVS}$(F,A))c;$\overline{CVS}$((F,A)c)=(CVS(F,A))c;
7) 幂等律:CVS(F,A)=CVS(CVS(F,A));$\overline{CVS}$((F,A))=$\overline{CVS}$($\overline{CVS}$(F,A))
性质2 当覆盖C是最细的粒度关系时,即C={{x1},{x2},…,{xn}}时,有:
CVS((F,A))=(F,A)=$\overline{CVS}$((F,A)),也就是说当粒度最细时,基于覆盖关系建立的粗糙Vague软集是可定义的。
性质(1)~性质(5)依据Vague软集的相关性质证明较为简单,从略。这里仅对性质(6)和(7)进行证明,如下所示:
性质(6)的证明过程如下:
由定义3可知:
(F,A)c为(F,A)的补,且有t(F,A)c(x)=f(F,A)(x),1-f(F,A)c(x)=1-t(F,A)(x),所以t(CVS(F,A))c(x)=f(CVS(F,A))(x)=inf{f(F,A)(y)|y∈∩Md(x)}=inf{t(F,A)c(y)|y∈∩Md(x)}=tCVS((F,A)c)(x)f(CVS(F,A))c(x)=t(CVS(F,A))(x)=sup{t(F,A)(y)|y∈∩Md(x)}=sup{f(F,A)c(y)|y∈∩Md(x)}=fCVS((F,A)c)(x)所以,CVS((F,A)c)=($\overline{CVS}$(F,A))c。同理可证,$\overline{CVS}$((F,A)c)=(CVS(F,A))c。
性质(7)的证明过程如下:由定义7可得
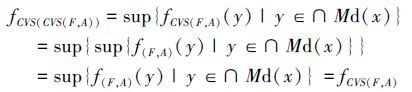
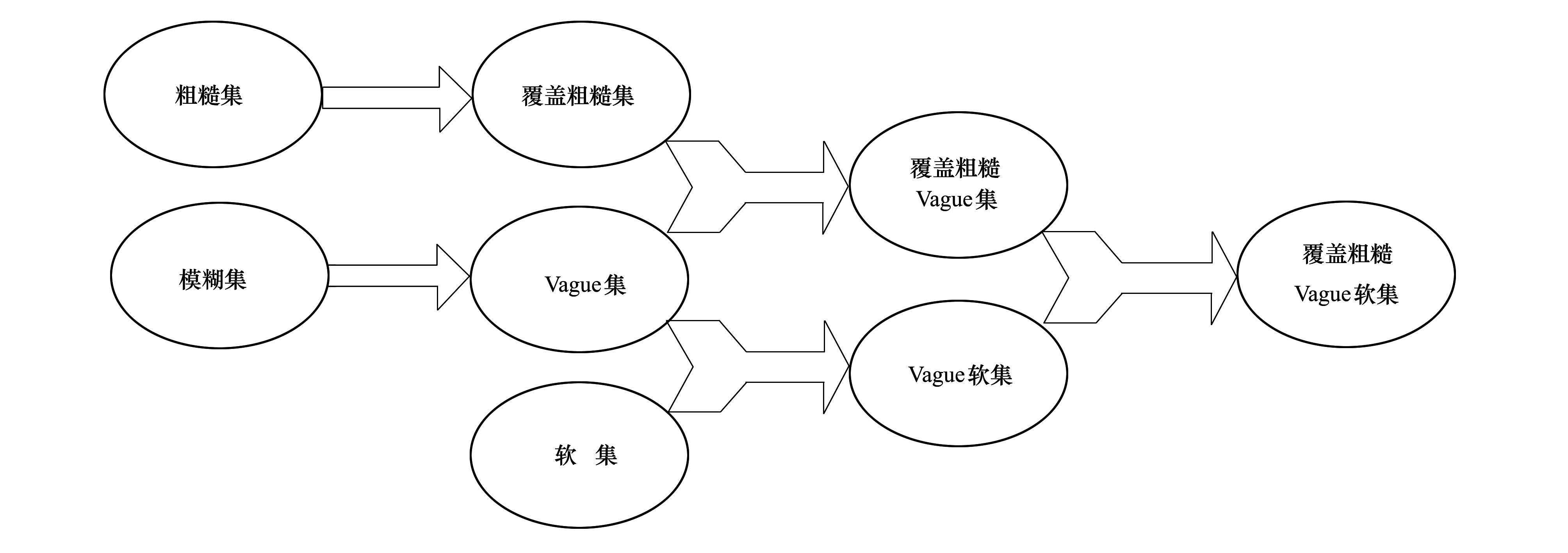
下面分别讨论Vague软集、覆盖粗糙Vague集和覆盖粗糙Vague软集的关系。3种模型都是机器学习领域处理不确定性信息的数学模型,但是根据上述3种模型的定义可以看出,Vague软集兼具Vague集和软集的代数特征,其本质是具有Vague集区间特征的软集。而覆盖粗糙Vague集兼具粗糙集和Vague集的代数特征,其本质是上下上近似算子均为Vague集的覆盖粗糙集。本文提出的覆盖粗糙Vague软集兼具粗糙集和Vague软集的代数特征,其本质是上下上近似算子均为Vague软集的覆盖粗糙集,是对覆盖粗糙Vague集和Vague软集的进一步推广和扩展。3种模型的关系如图 2所示。
|
| 图 2 3种模型之间的关系 |
引起覆盖粗糙Vague软集不确定性的因素主要有2个：①覆盖粒度空间的知识具有颗粒型。在具有较细关系的2个覆盖粒度空间上,其知识熵也具有偏序关系,即粒度空间越细,知识熵越大,覆盖粒度空间不确定性越小。反之,粒度空间越粗,知识熵越小,覆盖粒度空间不确定性越大。②其本身边界域的大小。因此类比经典粗糙集,通过覆盖粗糙Vague软集本身的代数特征来定义覆盖粗糙Vague软集本身的粗糙度。
3.1 知识熵定义10(知识熵) 设U为非空有限论域,C为U上的一个覆盖,则覆盖近似空间(U,C)的知识熵定义如下:
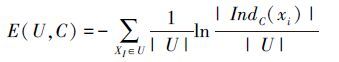
性质2[18]设U为非空有限论域,C为U上的一个覆盖,则覆盖近似空间(U,C)的知识熵具有如下性质:
1) 0≤E(U,C)≤log|U|;
2) 当∀xi∈U(IndC(xi)=U)时,E(U,C)取最小值0;
3) 当∀xi∈U(IndC(xi)=xi)时,E(U,C)取最大值log|U|。
定理1 设(U,C1)和(U,C2)为覆盖近似空间,若C1≤3C2,则有E(U,C1)≥E(U,C2)。证明参见文献[16]。
3.2 覆盖粗糙Vague软集的粗糙度定义11 (覆盖粗糙Vague软集的粗糙度)
设CVS=(CVS(F,A),$\overline{CVS}$(F,A))是给定论域U上的覆盖粗糙Vague软集,0<β≤α≤1,则有(F,A)的α下近似CVS(F,A)α
(F,A)的β上近似$\overline{CVS}$(F,A)β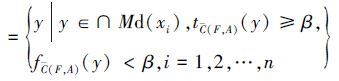
,
定义覆盖粗糙Vague软集的粗糙度如下:γα,βCVS=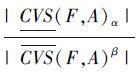
,ρα,βCVS=1-γα,βCVS;其中,0<β≤α≤1,$\overline{CVS}$(F,A)β≠φA。
下面定义基于熵的覆盖粗糙Vague软集不确定性度量方法:
定义12 设(U,C)为一覆盖近似空间,CVS=(CVS(F,A),$\overline{CVS}$(F,A))为论域U上的覆盖粗糙Vague软集,0<β≤α≤1,定义覆盖粗糙Vague软集一种不确定性度量为
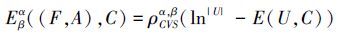
上述覆盖粗糙Vague软集的不确定性度量方法,既反映了覆盖粗糙空间的粒度大小也反映了覆盖粗糙Vague软集本身的粗糙度,因此可以度量覆盖粗糙Vague软集的不确定性。
4 算例分析例1 设论域(U,C)为检测到的7位胃病患者xi(i=1,…,7)的1组胃电信号(EGG),用一覆盖近似空间表示,记为U={x1,x2,…,x7},将7位胃病患者随机划分为2类,分别分析每类患者胃电信号数据的不确定性,用U上的2个覆盖分别表示为
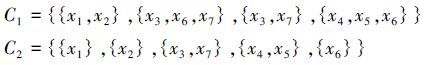
由于胃电信号(EGG)主要受电极摆放、胃的运动状态、胃壁位置变化3个参数影响,用Vague软集(F,A)表示为
知,C2≤3C1,由定义10计算知E(U,C1)=1.079;E(U,C2)=1.550,显然E(U,C1)<E(U,C2),表明覆盖越细,知识熵值越大,提供的信息量越多,不确定性越小,符合定理1。
由覆盖粗糙Vague软集定义可得
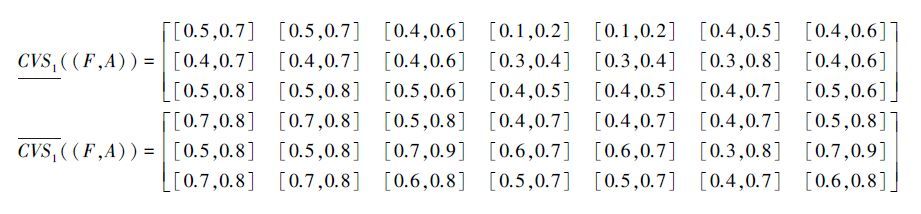
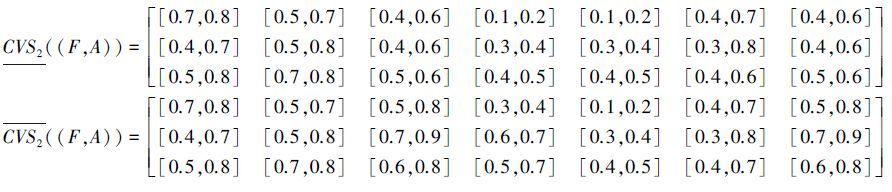
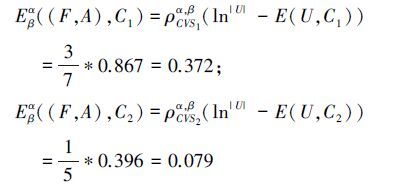
显然有结论:C2≤3C1,Eβα ((F,A),C2)<Eβα ((F,A),C1),表明覆盖越细,覆盖粗糙Vague软集不确定性度量值越小,不确定程度越小,因此可以采用本文的度量方式来度量覆盖粗糙Vague软集的不确定性程度。这是因为,基于覆盖的粗糙Vague软集的不确定性程度,不仅和它自身的粗糙度大小有关,还和覆盖的粗细有关。覆盖的粗细不同,对知识分类产生的不确定性的影响程度也不同。覆盖的粒度越细,其包含的信息量越多,熵值也就越大,知识的分辨能力就越强,加之本身的粗糙度也小,因此综合起来看,覆盖粗糙Vague软集模型的不确定程度越小;反之,粒度越大,其熵值越小,知识的分辨能力就越弱,加之本身的粗糙度也大,因此综合起来看,覆盖粗糙Vague软集模型的不确定程度越大。也就是说C1类患者胃电信号(EGG)的不确定性程度要大于C2类患者,这一结果可用于临床胃病辅助诊断。
5 结 论本文在覆盖粗糙集理论和Vague软集理论研究的基础上，在覆盖近似空间下将粗糙集与Vague软集进行融合，提出了一种新的处理不确定性信息的数学模型-基于近邻域的覆盖粗糙Vague软集，并给出了该模型满足的各类性质及证明。另外，结合覆盖近似空间下知识熵及覆盖粗糙Vague软集粗糙度的概念，提出了一种覆盖粗糙Vague软集的不确定性度量方法，并将该模型及其不确定性度量方法应用于胃电信号分析，实验表明，覆盖粗糙Vague软集模型为胃电信号处理及胃疾病辅助诊断问题提供了良好的理论工具和数学模型。
| [1] |
孔宪仁,徐大富. 空间系绳研究综述[J]. 航天器环境工程, 2010, 27(6): 0775-0783 Kong Xianren, Xu Dafu. The Studies of Space Tether[J]. Spacecraft Environment Engineering, 2010, 27(6): 0775-0783 (in Chinese) |
| [2] | Vladimir Aslanov, Alexander Ledkov. Dynamics of Tethered Satellite Systems[M]. Russia, Woodhead Publishing Ltd, 2012 |
| [3] |
崔本廷. 空间绳系的控制与应用[D]. 长沙:国防科学技术大学, 2006 Cui Benting. The Control and Application of Thethered System[D]. Changsha, National University of Defense Technology, 2006 (in Chinese) |
| Click to display the text(9) | |
| [4] | Rupp C C. A Tether Tension Control Law for Tethered Satellite Deployed along Local Vertical[R]. Marshall Space Flight Center, NASA TM X-64963, 1975 |
| [5] |
于绍华. 绳系卫星系统二维平面运动和常规动力学[J]. 宇航学报, 2000(4):15-24 Yu Shaohua. Regular Dynamics of In-Planar Motion of Tethered Satellite System[J]. Journal of Astronautics, 20004: 15-24 (in Chinese) |
| Cited By in Cnki (27) | |
| [6] | Pradeep S. A New Tension Control Law for Deployment of Tethered Satellites[J]. Mechanics Research Communications, 1997, 24(3): 247-254 |
| Click to display the text | |
| [7] | Jin D P, Hu H Y. Optimal Control of a Tethered Subsatellite of Three Degrees of Freedom[J]. Nonlinear Dynamics, 2006, 46: 161-178 |
| Click to display the text | |
| [8] |
文浩,金栋平,胡海岩. 基于微分包含的绳系卫星时间最优释放控制[J]. 力学学报,2008,40(1):135-140 Wen Hao, Jin Dongping, Hu Haiyan. Time-Optimal Deployment of a Tethered Subsatellite Based on Differential Inclusion[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008,40(1):135-140 (in Chinese) |
| Cited By in Cnki (18) | |
| [9] | Beletsky V, Levin E M. Dynamics of Space Tether Systems[M]. Russia: Amer Astronautilcal Society, 1993 |
| [10] |
扎伯罗特诺夫·尤里著. 空间系绳系统运动动力学与控制导论[M]. 王长青,译. 科学出版社, 2013 Zablotnov Yuriy. Introduction to Dynamics and Control in Space Tether System[M]. Wang Changqing Translator. Beijing, Science Press, 2013 (in Chinese) |
