一阶导数的解算有着十分广泛的应用，比如，在气象、化学、地质学、航空航天、工程力学、机械制造等众多领域都有很高的应用价值。在这些工程应用中，测量数据经常以离散点的形式给出，往往需要用近似函数对其进行拟合，并进行微分，才能获得其一阶导数。在应用数学领域，像这样通过离散点上的观测值来求取观测量的近似(偏)导数问题称为数值微分问题[1]。数值微分往往是不适定的[1]。由于测量数据变化规律的复杂性、拟合模型的近似性、算法的局限性以及测量误差的影响，要获得准确的计算结果具有相当的难度，因此，离散数据的一阶导数解算在某些领域一直是工程计算中的难点。
为了能够对测量数据进行尽可能准确的微分，人们尝试了许多方法以提高解算精度，主要有以下几种方法：①尽量采用一些逼近程度好的模型，比如多项式最优线性滤波[2]、分段曲线拟合[3]；②采用一些正则化[1]调整算子，如积分算子[4]；③采取一些特殊的技巧，如样条拟合[5]、自适应学习算法[6]等。这些算法的基本特征是用近似函数对测量数据进行拟合，然后按照一定的原则在近似函数上找到一点，把该点的微分结果作为测量数据在该点的微分结果，必要时对微分结果进行优化。通过多方努力，很多微分算法在理论上获得了“最佳逼近”的效果，即在理论上无限趋近于“真值”。2004年，差值定理及其推论[7]的发现，从另一个角度改善了“最佳逼近”的效果，以至于在理论上达到了“相等”，而非“无限逼近”，即在测量数据连续且可导、测量误差为零的理想条件下，微分结果与“真值”是相等的，为解决数值微分问题提供了良好的途径。由于采用差值定理及其推论对一阶导数进行解算时，算法误差为零，使得不适定问题转化为了适定问题，获得了理想情况下数值微分的精确解，因此具有很大的优越性，在离散数据一阶导数解算的实际应用中，不仅能有效降低数据剧烈变化段微分求导的截断误差，而且受近似函数的形式及拟合区间的大小等因素的影响很小，解算精度很高，具有良好的适应性、稳定性。但是，在工程实践中，实测数据所包含的测量误差不仅会降低计算结果的准确度，而且可能导致某些测量数据不满足差值定理的应用条件，无法得到一阶导数，因此，怎样才能减小或消除测量误差的影响，获得理想的解算结果就成了需要研究的课题。本文立足于此，对差值定理用于离散数据一阶导数解算的适用条件进行了分析和比较，找到了比较实用的算法。
1 差值定理及其物理意义差值定理的基本内容是:设函数F(t)和f(t)在某定义域Ω内的任一点均存在n阶导数,且G(t)=F(n-1)(t)-f(n-1)(t),则F(n)(t0)=f(n)(t0) ⇔G′(t0)=0 (t0∈Ω)。其推论为:设函数G(t)=F(t)-f(t)的定义域为Ω,且函数F(t)和f(t)的一阶导数、二阶导数均存在,则F′(t1)=f′(t1)⇔G′(t1)=0(t1∈Ω)且F″(t2)=f″(t2)⇔G″(t2)=0(t2∈Ω)。
对于差值定理及其推论的物理意义,文献[7]中的表述为“差值定理表明:2个函数n阶导数相等的点是它们的n-1阶导数的差值的极值点;其推论表明:2个函数的一阶导数相等的点是它们的差值曲线的极值点,二阶导数相等的点是它们的差值曲线的拐点”。该表述忽略了“导数为零的点不一定是极值点”的特殊情况。因此,差值定理及其推论的物理意义应表述为“2个函数的n-1阶导数的差值的驻点是它们的n阶导数相等的点;2个函数的差值曲线的驻点是它们的一阶导数相等的点,差值曲线的拐点是它们的二阶导数相等的点。”由于极值点即为驻点,所以,应用差值定理及其推论进行一阶导数解算时,只要求出测量数据与拟合数据的差值曲线的极值点,即可把拟合数据在该极值点处的一阶导数作为测量数据在该点的微分结果。在工程实际中,判别差值曲线的极值点比判别其他形式的驻点更容易把握,因此,本文主要基于极值点进行讨论。
2 差值定理的适用条件解析 2.1 差值定理的适用条件应用差值定理及其推论进行一阶导数解算时,判别差值曲线的极值点可尝试采用如下2种判别条件:
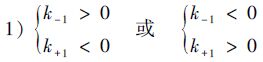
采用斜率判别条件时,不需要知道差值曲线上每一点的斜率的确切值,而只需要知道与极值点相邻的点的斜率孰大孰小即可。
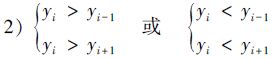
根据1)中的判别条件,在不考虑测量误差的情况下,可推出差值曲线上下标为0的点是极大值点时
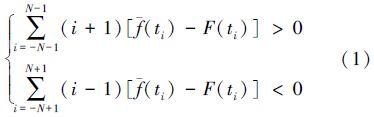
采用某组实测数据,以(1)式和(2)式为差值定理及其推论的适用条件判别差值曲线的极值点,进行一阶导数解算,改变对差值曲线进行直线拟合的滤波半径,将解算的数据点数列入表 1。
由表 1可以看出,当滤波半径不变时,并不是所有的测量点都能获得一阶导数的解算结果。
如图 1所示,在离散情况下,A为极值点,而点B和点C的斜率均小于0,所以无法正确判别出极值点。因此,当离散点出现如图 1所示的极限情况时,极值点A不能够被有效判别。这是表 1中有一些数据点没有解算结果的原因。
|
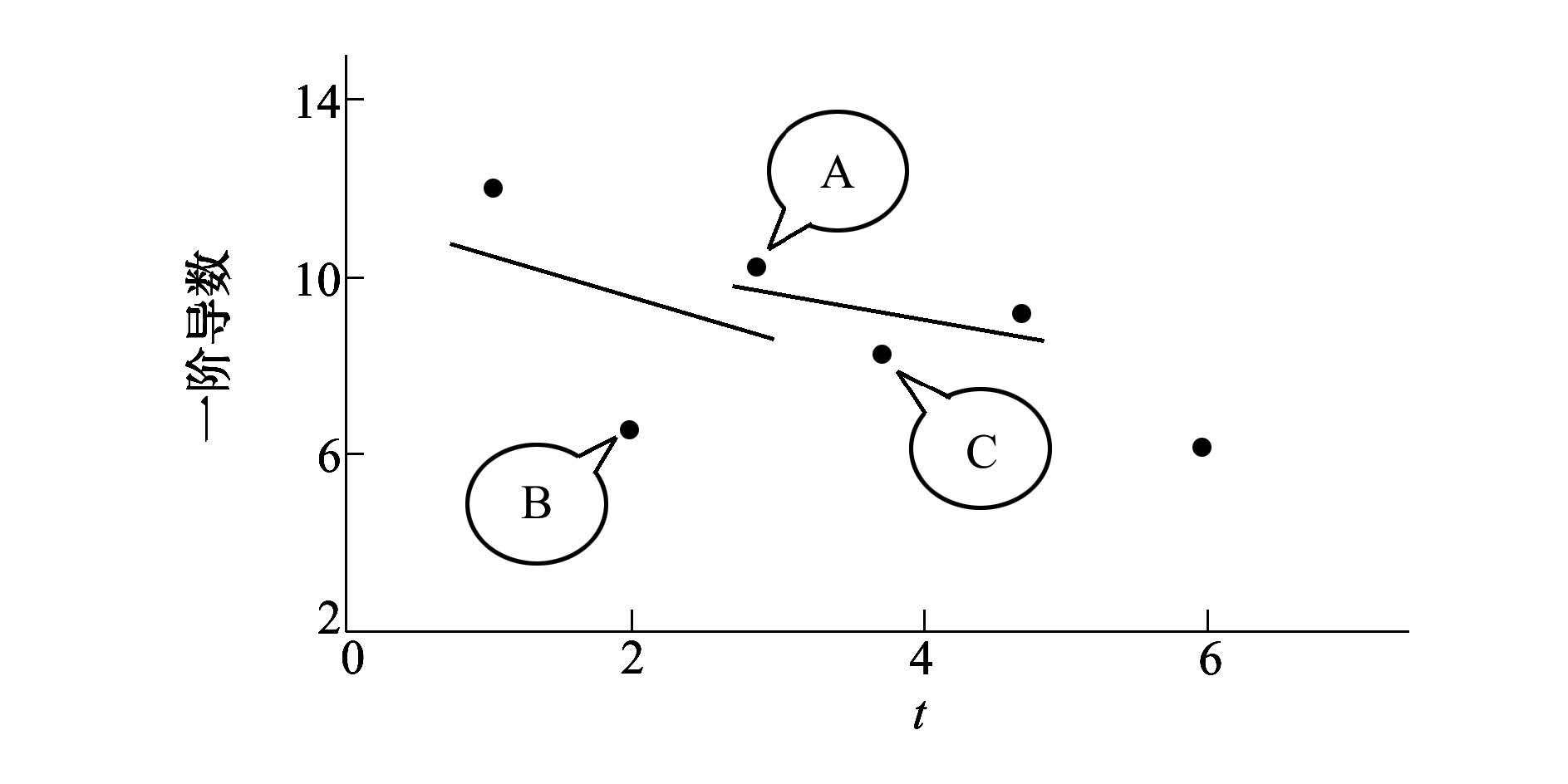
| 图 1 部分数据无解算结果的原因分析示意图 |
由表 1可知,将不同滤波半径的解算结果合并后,则可能获得所有测量数据的一阶导数解算结果,也就是说,调节直线拟合的滤波半径后重新解算,可以弥补原来未解算出来的数据。
由(1)式和(2)式可以看出,当测量数据等间隔采样时,若采用中心平滑直线拟合法求解测量数据与近似拟合函数的差值曲线上的极值点,则判别条件与采样间隔的大小无关,与测量值、近似函数值和直线拟合的滤波半径有关。因此,调节滤波半径N,有可能使判别极值点的充要条件得到满足,从而使一些无法解算的测量数据获得一阶导数解算结果。
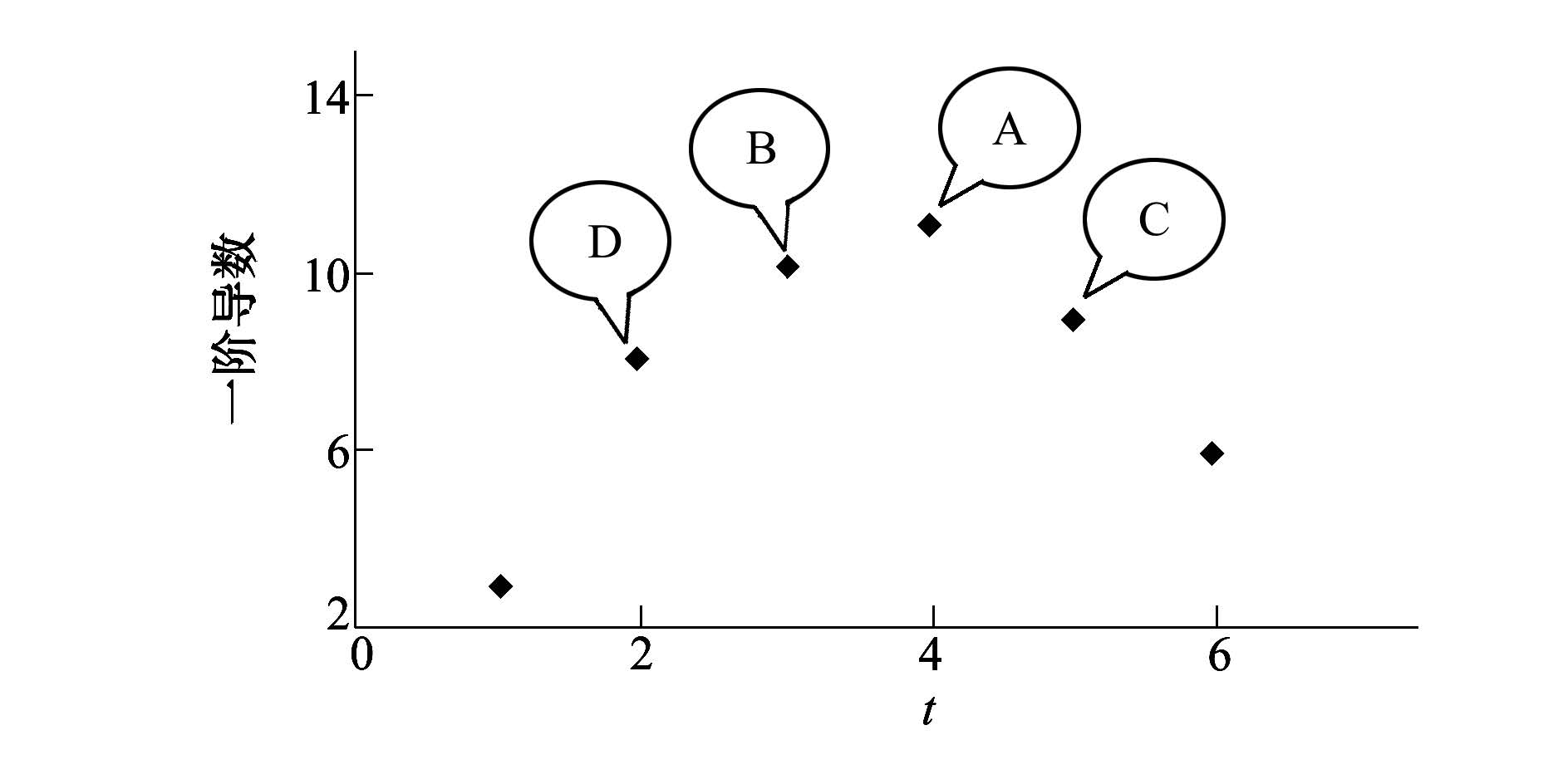
对于离散数据极值点的判别条件是取目标点的前一点和后一点各自的斜率是否为异号,这其实是一种比较模糊的判别方法。当采样率足够大时,这种算法判别得到的所谓“极值点”是真正的极值点的临近的一个离散点,而且,由于受斜率判别的影响,该点不一定是离散点中的“极值点”,如图 2所示。
|
| 图 2 极值点分析示意图 |
在图 2中,目测很明显点A为离散点中的极值点,但点D处的斜率为正值,点A处的斜率为负值,若按照判断条件,则点B为极值点,显然与实际情况不符。因此,从严格意义上讲,“目标点的前一点和后一点各自的斜率异号”只是判别极值点的必要条件,而非充分条件。
2.3 极值判别条件解析根据2)中的判别条件,可推出差值曲线上下标为i的点是极大值点的充要条件是
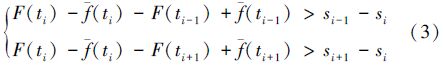
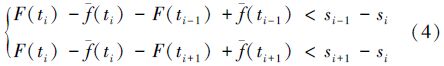
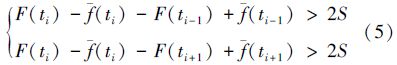
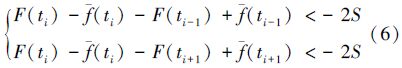
由于测量数据往往是离散的,差值曲线的极值点受测量值和拟合值的影响,可能位于离散点处,也可能位于2个离散点之间,故使用上述方法判断出来的极值点并不一定是真正的“极大值点”或“极小值点”,而极有可能是真正的极值点附近的比较接近于极值点的离散点,在测量数据的差值曲线上,我们仅近似地把它看作是极值点。因此,称文中所说的极值点为“近似极大值点”或“近似极小值点”更为贴切。
3 差值定理的应用方法 3.1 分析与推导上述分析表明,当差值曲线极值点与其邻点数值之差大于测量误差限的2倍时,斜率法可能会造成极值点的误判;当差值曲线极值点与其邻点数值之差小于测量误差限的2倍时,极值点不能确定。故在测量误差允许的情况下采用极大或极小值的直接判别法,比斜率参与判别的方法更有效。因此,推荐使用极值判别条件,当求出拟合值F(t)后,根据(5)式和(6)式找到差值曲线的近似极值点,即可根据差值定理得到该点的一阶导数。
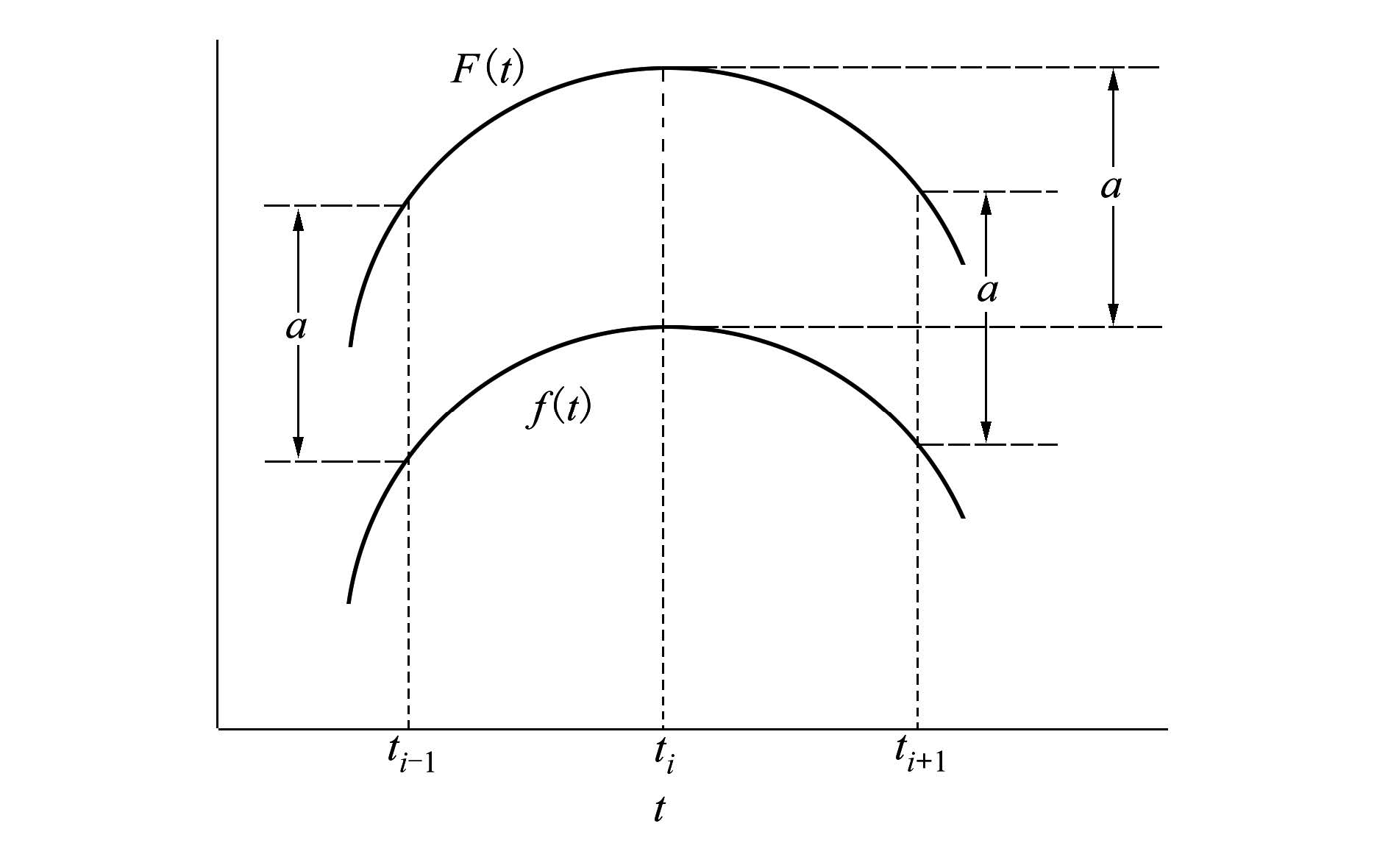
由于利用差值定理解算一阶导数时,测量数据在差值曲线极值点处的一阶导数值由拟合曲线在该点的一阶导数值决定,所以在极值点处,测量数据的一阶导数的解算精度只与测量值的一阶导数和拟合曲线的一阶导数的局部接近程度有关,因此,考虑2点:①采用最小二乘法来构造拟合曲线F(t),使之与测量曲线有较好的接近程度,且由于利用差值定理进行一阶导数解算时,解算精度受拟合模型的影响较小,因此,综合考虑解算精度和解算速度,可采用三次多项式作为拟合模型;②考虑到测量数据是离散的,很可能会导致判断出来的差值曲线的极值点偏离真正的极值点而引起一阶导数的解算结果产生误差,为尽量减小这种误差,应使差值曲线极值点附近拟合曲线与测量曲线的曲率有较好的吻合度,即应使拟合值尽可能满足或接近(7)式
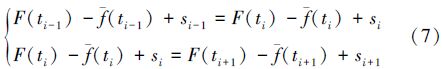
令f(ti)=-f(ti)-si,f(ti)为测量值-f(ti)所对应的真值,则(7)式所表达的状态如图 3所示:
即
|
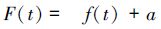
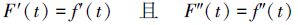
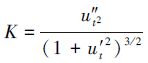
| 图 3 曲率吻合示意图 |
将(7)式与(3)式和(4)式比较可知,(7)式是(3)式和(4)式的极限情况,因此可合成下式:
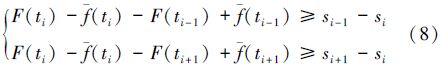
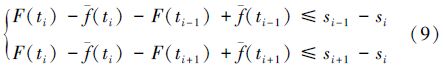
(8)式及(9)式即为满足差值定理条件,使得拟合值与测量值的差值曲线的一阶导数为零的点,一般为极值点,也可能是其它形式的驻点。
若有的点在差值曲线上没有对应的驻点,虽然可通过改变拟合区间的长度或拟合模型来使该点成为驻点,但在工程应用上难以把握,因此,考虑采用系数调节法来改变多项式的系数,使得该点成为驻点。
令
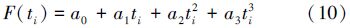
将(10)式代入(8)式和(9)式,得
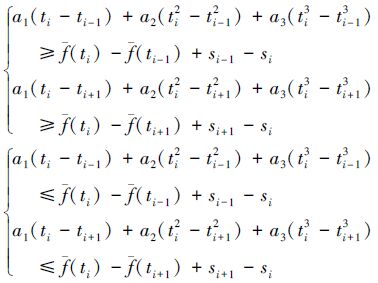
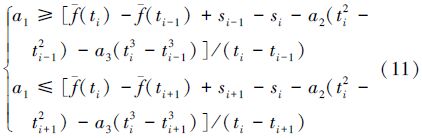
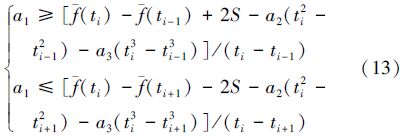
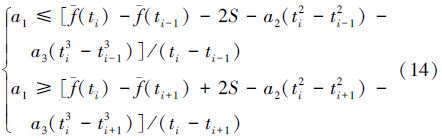
假设测量数据为等间隔采样,则(15)式可化为
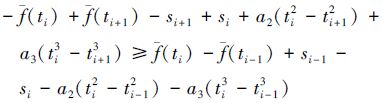
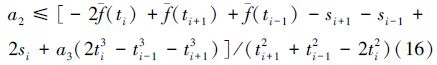
把测量误差限S代入(16)式,得
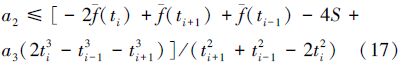
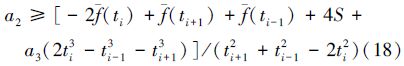
由(7)式和(10)式可知,当a0、a3固定时,若a1、a2是方程组的解,可使拟合曲线与测量曲线在点i附近的曲率获得较好的吻合度。因此,a1与a2的取值应尽可能满足或接近(7)式的解。
由(7)式和(10)式得
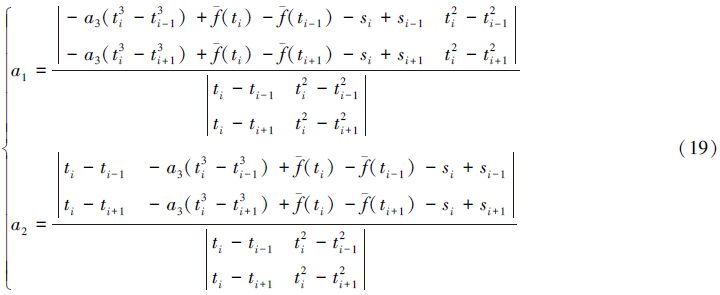
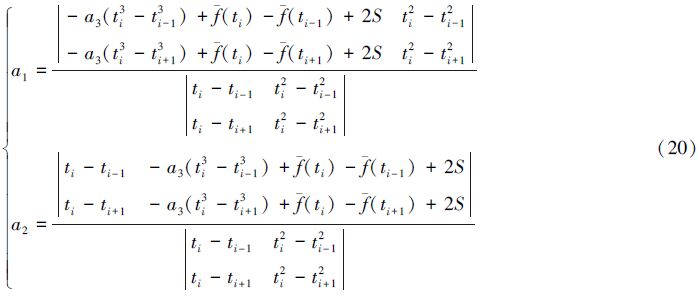
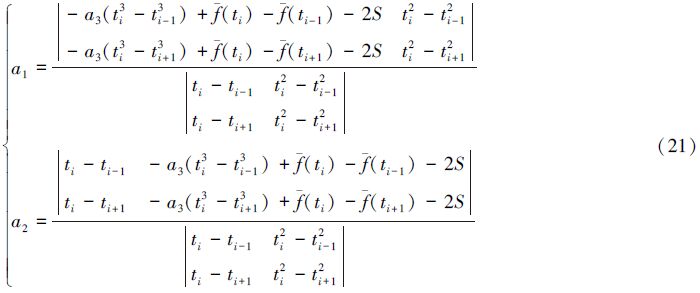
上述分析表明:按(13)式、(17)式或(14)式、(18)式选取a1、a2的值,可使没有在差值曲线上取到近似驻点的测量数据能够取到近似驻点;按(20)式或(21)式可获得更好效果,使拟合曲线与测量曲线在驻点附近的曲率尽可能接近或吻合。
综上所述,利用差值定理进行下标为i的离散数据一阶导数解算时,可采用下列步骤:
1) 选取拟合区间,进行最小二乘三次多项式拟合,获得拟合多项式的系数A0、A1、A2、A3,它们分别表示常数项、一次项系数、二次项系数和三次项系数;
2) 根据(20)式或(21)式确定调整后的系数a1、a2;
3) 计算拟合多项式F(t)=A0+a1t+a2t2+A3t3在点i处的一阶导数,即可作为该处测量数据的一阶导数。
上述的系数调节法对于在差值曲线上能够获得近似驻点的测量数据也同样适用,可使拟合曲线上该点附近的曲率与测量曲线的曲率尽可能接近或吻合,获得更高的解算精度。因此,可依此计算拟合区间内不包括端点的所有点的一阶导数。
3.2 仿真计算与讨论
1) 对于表 2中的仿真数据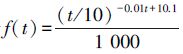
+100 000,采用三次多项式最小二乘法进行拟合,得多项式系数为
| t | f(t) | f(t)的一阶导数真值 | f(t)的拟合值 | 差值 |
| 30.000 | 100 047.401 | 14.964 | 100 046.182 | -1.219 |
| 31.000 | 100 064.630 | 19.679 | 100 065.797 | 1.168 |
| 32.000 | 100 087.170 | 25.627 | 100 088.422 | 1.252 |
| 33.000 | 100 116.381 | 33.066 | 100 116.662 | 0.281 |
| 34.000 | 100 153.898 | 42.295 | 100 153.123 | -0.776 |
| 35.000 | 100 201.680 | 53.656 | 100 200.411 | -1.269 |
| 36.000 | 100 262.051 | 67.543 | 100 261.133 | -0.919 |
| 37.000 | 100 337.756 | 84.402 | 100 337.894 | 0.138 |
| 38.000 | 100 432.013 | 104.737 | 100 433.301 | 1.288 |
| 39.000 | 100 548.577 | 129.116 | 100 549.959 | 1.382 |
| 40.000 | 100 691.802 | 158.172 | 100 690.476 | -1.327 |
|
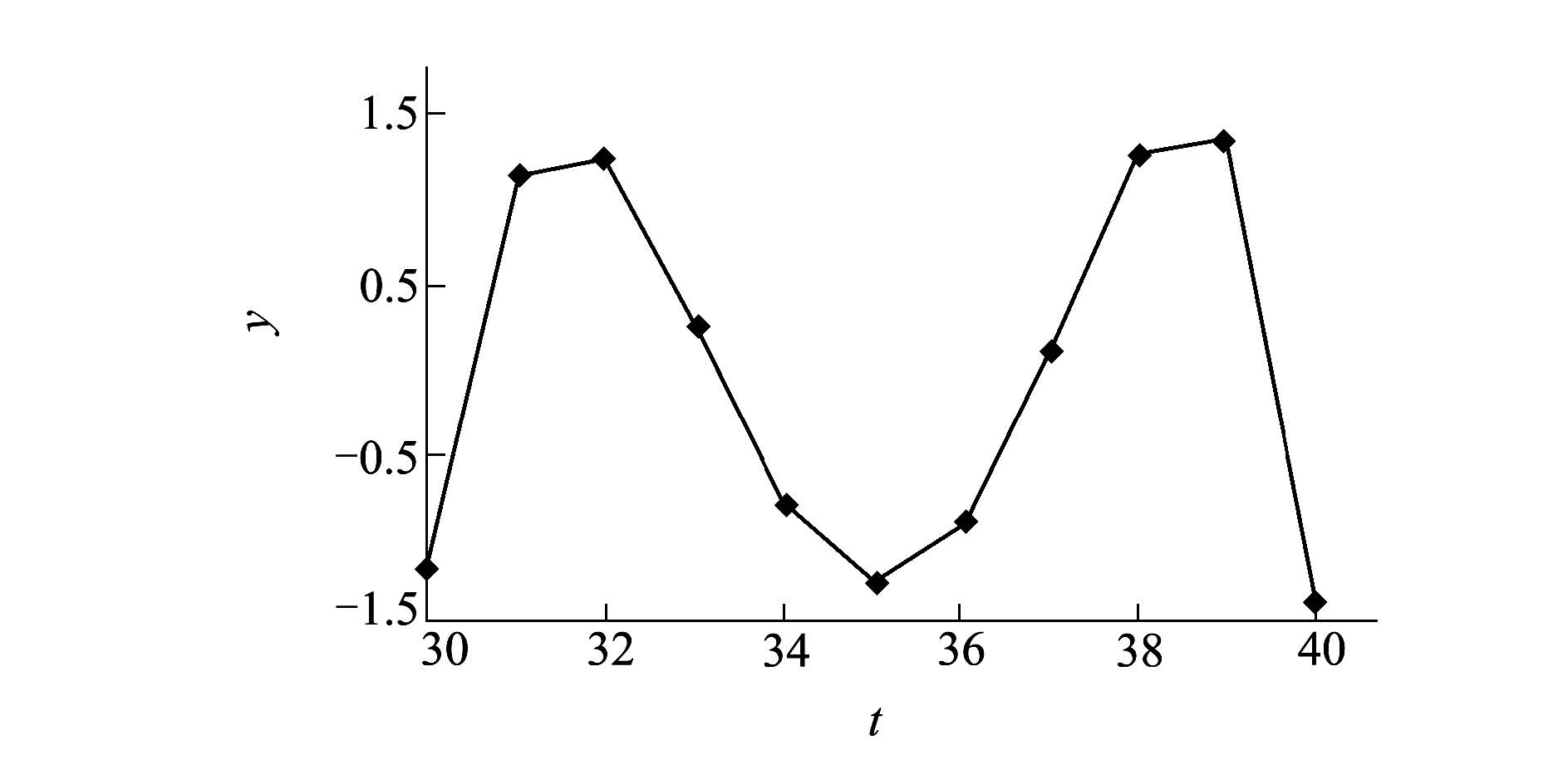
| 图 43次多项式拟合的差值曲线图 |
如表 2和图 4所示,差值曲线极值点的横坐标是t=32、35、39。以横坐标为37的点为例,利用(17)式和(13)式对拟合多项式A0+A1t+A2t2+A3t3的系数进行调节:在S=0.000 01的情况下,根据(17)式得
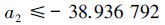
根据(13)式得
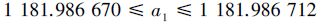
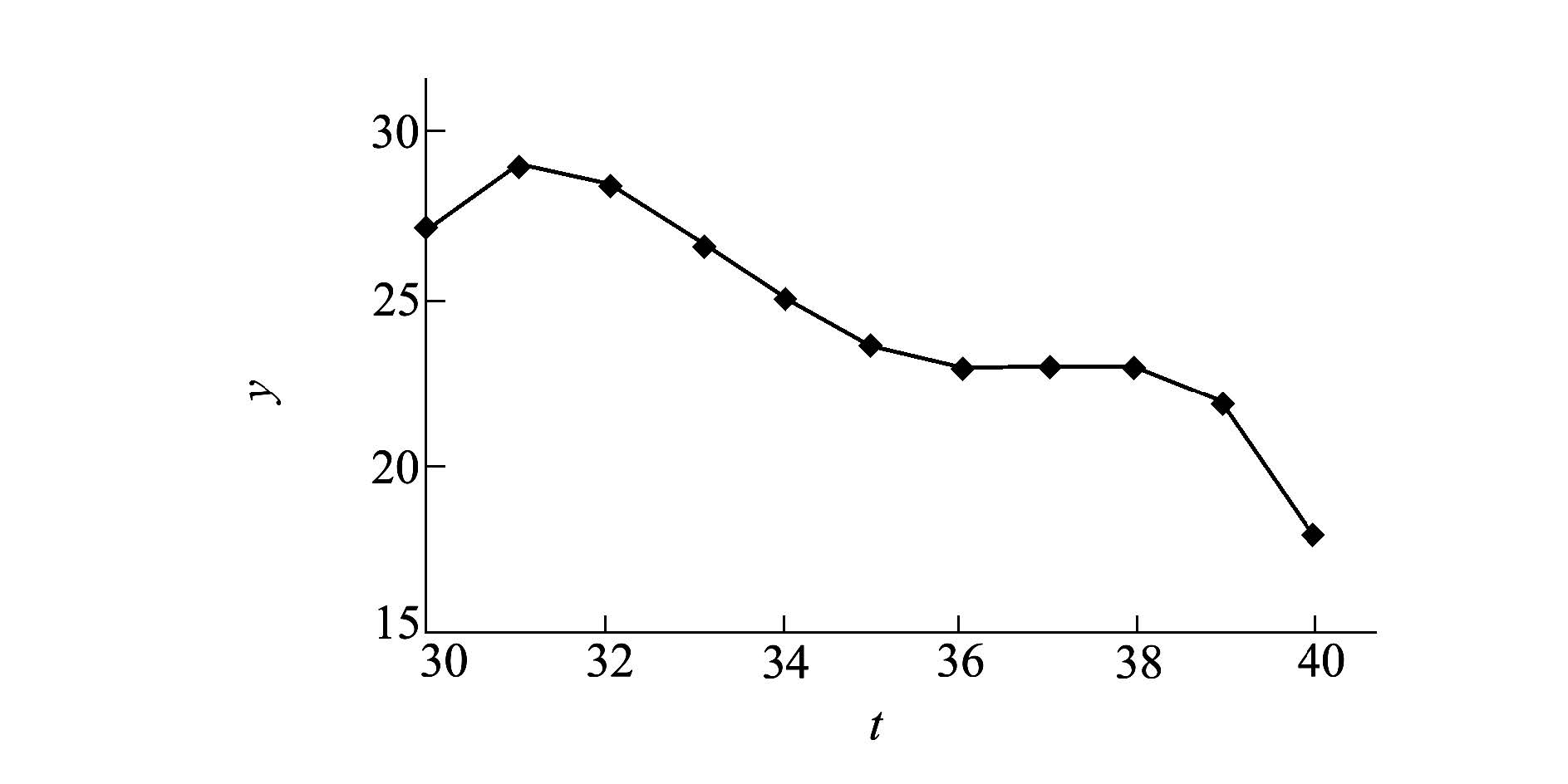
将A0=87 930.576 404 105、a1=1 181.987、a2=-38.937、A3=0.434 351 685作为拟合多项式系数进行计算,结果列入表 3,并将差值绘入图 5。
| t | f(t) | 拟合值 | 差值 |
| 30.000 | 100 047.401 | 100 074.559 | 27.158 |
| 31.000 | 100 064.630 | 100 093.677 | 29.047 |
| 32.000 | 100 087.170 | 100 115.710 | 28.540 |
| 33.000 | 100 116.381 | 100 143.267 | 26.885 |
| 34.000 | 100 153.984 | 100 178.950 | 25.051 |
| 35.000 | 100 201.680 | 100 225.368 | 23.687 |
| 36.000 | 100 262.051 | 100 285.126 | 23.074 |
| 37.000 | 100 337.756 | 100 360.830 | 23.075 |
| 38.000 | 100 432.013 | 100 455.087 | 23.745 |
| 39.000 | 100 548.577 | 100 570.503 | 21.926 |
| 40.000 | 100 691.802 | 100 709.683 | 17.881 |
|
| 图 5 以t=37为目标点调整多项式系数后的差值曲线图 |
由表 3和图 5可看出,按(17)式和(13)式对拟合多项式的系数A1和A2进行调整后,仿真数据与拟合多项式的差值曲线在t=37处以微小的差别获得了极大值点。一阶导数的解算结果为a1+2a2t+3A3t2=84.546,误差为0.145,解算效果良好。
2) 取S=20.0,按照(20)式确定的多项式系数调节方法及3.1节中应用差值定理对一阶导数进行解算的步骤,对表 2中的仿真数据f(t)拟合区间中不包括端点的所有数据进行一阶导数计算,结果列入表 4。
从表 4中的数据可以看出,采用3.1节中的方法的确可以构造三次多项式,使拟合区间中不包括端点在内的任一点成为差值曲线的极值点,且解算精度及稳定性总体上优于未经系数调节获得的极值点,并且使和端点临近的点获得几乎同样好的精度。
| t | 调整后的系数a2 | 调整后的系数a1 | 调整系数后的一阶导数计算误差 | 未调整系数的一阶导数计算误差 |
| 31.000 | -77.739 | 3 587.015 | -0.229 | -0.549 |
| 32.000 | -78.363 | 3 706.317 | -0.186 | -0.630 |
| 33.000 | -78.847 | 3 817.830 | -0.136 | -0.718 |
| 34.000 | -79.172 | 3 919.566 | -0.079 | -0.078 |
| 35.000 | -79.312 | 4 009.262 | -0.014 | -0.085 |
| 36.000 | -79.243 | 4 084.360 | 0.061 | -0.092 |
| 37.000 | -78.937 | 4 141.985 | 0.145 | -0.100 |
| 38.000 | -78.363 | 4 178.924 | 0.239 | -0.844 |
| 39.000 | -77.488 | 4 191.606 | 0.345 | -0.962 |
3) 取不同的S值,按照(20)式确定的多项式系数调节方法及3.1节中应用差值定理对一阶导数进行解算的步骤,对表 2中的仿真数据f(t)拟合区间中不包括端点的所有数据进行一阶导数计算,结果列入表 5。
| t | 一阶导数真值 | 调整系数后的一阶导数拟合值(S=0.8) | 调整系数后的一阶导数拟合值(S=20.0) | 调整系数后的一阶导数拟合值(S=100.0) |
| 31.000 | 19.679 | 19.450 | 19.450 | 19.450 |
| 32.000 | 25.627 | 25.441 | 25.441 | 25.441 |
| 33.000 | 33.066 | 32.930 | 32.930 | 32.930 |
| 34.000 | 42.295 | 42.215 | 42.215 | 42.215 |
| 35.000 | 53.656 | 53.642 | 53.642 | 53.642 |
| 36.000 | 67.543 | 67.603 | 67.603 | 67.603 |
| 37.000 | 84.402 | 84.546 | 84.546 | 84.546 |
| 38.000 | 104.737 | 104.976 | 104.976 | 104.976 |
| 39.000 | 129.116 | 129.460 | 129.460 | 129.460 |
从表 5中的数据可看出,当采用3.1节中的步骤对一阶导数进行解算时,测量精度对于计算结果没有影响。
设采样间隔为h,令
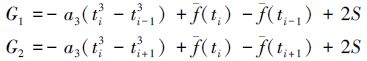
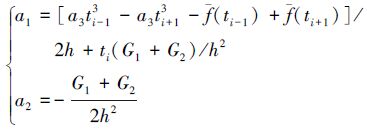
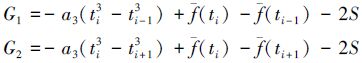
从(22)式中可看出,一阶导数的解算结果与测量误差限无关,表明3.1节中的一阶导数解算步骤基本可以消除测量误差的影响。(22)式还表明一阶导数的解算结果与a3的取值有关,由于a3是在最小二乘条件下获得的拟合多项式的系数,从中可看出最小二乘算法为解算结果的准确度所做出的巨大贡献。
3.3 实测数据验证以(5)式或(6)式作为离散状态差值曲线近似极值点的判断条件,应用差值定理及其推论,在不同的测量精度下,以10个测量点为拟合区间,以三次多项式作为拟合模型在最小二乘条件下对一组测量数据进行一阶导数解算;完成某个拟合区间的计算后,即把拟合区间向后移动继续计算,然后把各个区间的一阶导数解算结果合并在一起,获得整段数据的解算结果。解算结果的点数列入表 6。
将表 6中S=0.001的解算结果绘入图 6。
|
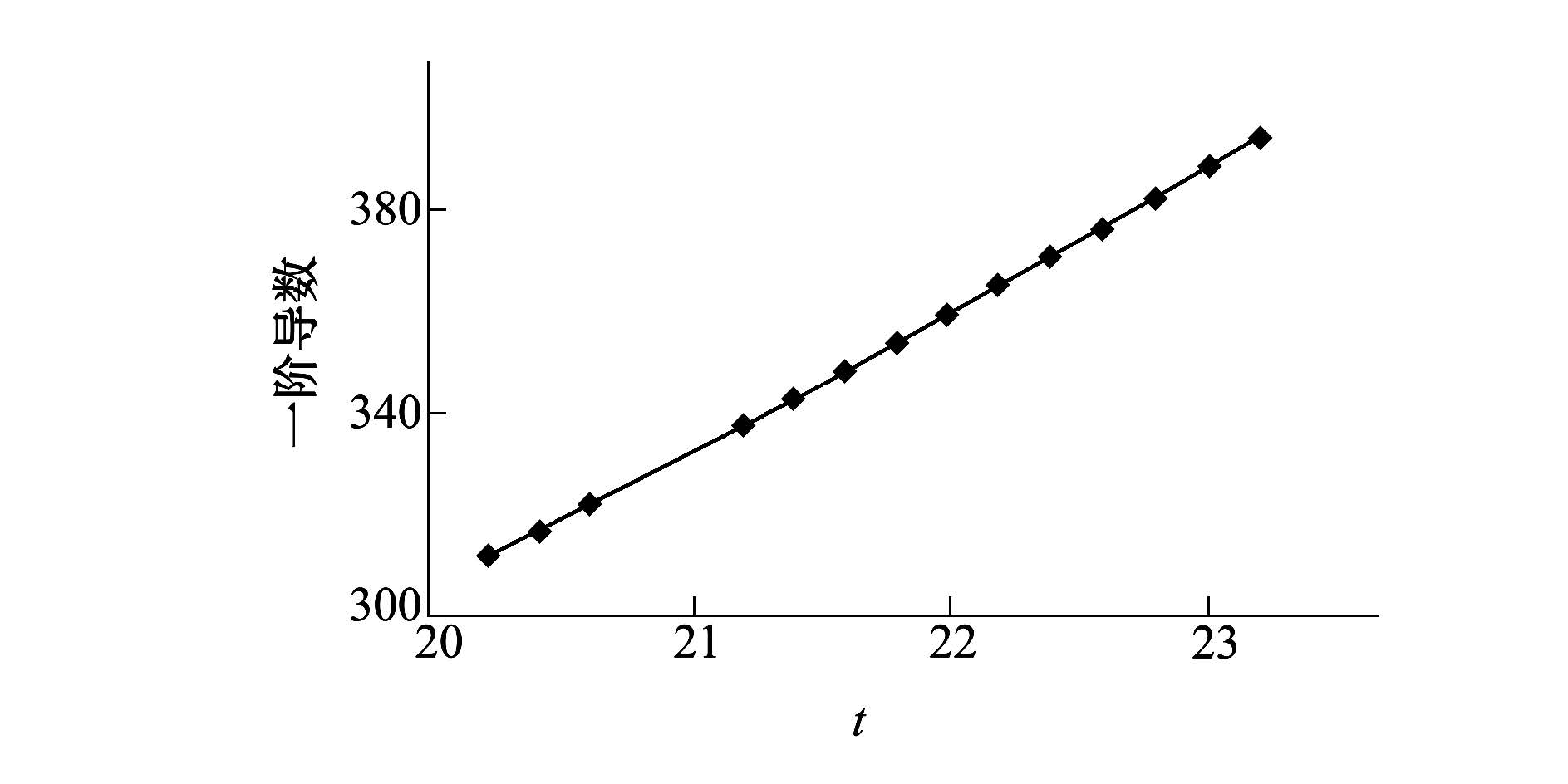
| 图 6 未调整多项式系数时的解算结果 |
将该组实测数据分为1～10点、9～18点2个区间,分别用最小二乘算法进行三次多项式拟合,得到2段的系数分别为A3(1～10点)=0.632,A3(9～18点)=0.076,再根据(22)式计算一阶导数,将结果绘入图 7。
|
| 图 7 调整多项式系数后的解算结果 |
比较图 6和图 7可知,在最小二乘拟合条件下,采用(22)式进行实测数据的一阶导数解算,不仅能够计算拟合区间内不包括端点的所有点的一阶导数,而且解算精度良好。
4 结 论差值定理及其推论在离散数据一阶导数解算中的适用条件为：
1) 离散状态差值曲线上下标为 的点为近似极大值点的充要条件是(3)式，为近似极小值点的充要条件是(4)式。
2) 离散状态差值曲线上下标为i的点为近似极大值点的充分条件是(5)式，为近似极小值点的充分条件是(6)式。
3) 当采用三次多项式对测量数据进行最小二乘拟合时，在等间隔采样条件下，保持拟合多项式的常数项和三次项系数不变，则按(13)式和(17)式调整一次项系数和二次项系数，可使下标为i的点成为差值曲线的极大值点，按(14)式和(18)式调整一次项系数和二次项系数，可使下标为i的点成为差值曲线的极小值点，而按(20)式或(21)式调整一次项系数和二次项系数，则在总体上可获得更好的一阶导数解算结果。
4) 利用差值定理进行下标为i的点的离散数据一阶导数解算时，在等间隔采样条件下，可采用下列步骤：
①选取N(N≥5)点拟合区间,进行最小二乘三次多项式拟合,获得拟合多项式的三次项系数A3;
②计算式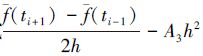
的值,作为测量数据点i处的一阶导数,其中,i不包括端点。
③将拟合区间向后滑动,用上述方法继续计算,直至完成不包括端点的所有测量数据的一阶导数解算。
5)按4)中方法进行一阶导数解算,可不受测量误差限的影响,获得不包括端点在内的所有测量数据的一阶导数,解算精度只与测量值、采样间隔和三次拟合多项式的三次项系数有关,解算结果整体上比差值定理算法更准确,更稳定,且可以良好的解算精度获得端点附近数据的一阶导数。
| [1] | 王业桂,蔡其发,黄思训. 一种气象观测数据求导的新方法[J]. 物理学报, 2010, 59(6): 4359-4368 Wang Yegui, Cai Qifa, Huang Sixun. A New Method for Calculating the Derivation of Meteorological Observational Data[J]. Acta Physica Sinica, 2010, 59(6): 4359-4368 (in Chinese) |
| Cited By in Cnki (6) | |
| [2] | 孙中豪,杜娟,王子龙. 基于白噪声正交多项式滤波的GPS测速方法分析[J]. 测绘地理信息,2013,38(5):21-24 Sun Zhonghao, Du Juan, Wang Zilong. Analysis of GPS Velocimetry Method Based on White Noise Orthogonal Polynomial Filtering[J]. Journal of Geomatics, 2013, 38(5): 21-24 (in Chinese) |
| Cited By in Cnki (1) | |
| [3] | 吕游. 基于过程数据的建模方法研究及应用[D]. 北京: 华北电力大学, 2014 Lü You. The Research and Application of Data-Based Process Modeling Method[D]. Beijing, North China Electric Power University, 2014 (in Chinese) |
| Cited By in Cnki (2) | |
| [4] | 刘继军. 不适定问题的正则化方法及应用[M]. 北京:科学出版社,2005 |
| [5] | 刘也,朱炬波,梁甸农. 递推样条滤波的工程化应用研究[J]. 宇航学报,2010,31(12): 2794-2800 Liu Ye, Zhu Jubo, Liang Diannong. Research of Recursive Spline Filter for Engineering Applications[J]. Journal of Astronautics,2010,31(12):2794-2800 (in Chinese) |
| Cited By in Cnki (4) | |
| [6] | 袁莉,刘宏伟,保铮. 雷达高分辨距离像分类器的参数自适应学习算法[J]. 电子与信息学报, 2008,30(1):198-202 Yuan Li, Liu Hongwei, Bao Zheng. Adaptive learning of Classifier Parameters for Radar High Range Resolution Profiles Recognition[J]. Journal of Electronics & Information Technology, 2008,30(1):198-202 (in Chinese) |
| Cited By in Cnki (24) | |
| [7] | 梁红. 利用差值定理降低飞行器速度和加速度拟合的截断误差[J]. 飞行器测控学报,2005,24(3):51-54 Liang Hong. Using Error Theorem to Reduce the Truncation Error Produced in Calculating the Velocity and Acceleration of Spacecraft[J]. Journal of Spacecraft TT & C Technology, 2005, 24(3): 51-54 (in Chinese) |
