超分辨率(SR)图像重建是指用图像处理的方法,通过软件算法的方式将低分辨率(LR)图像转换成高分辨率(HR)图像的技术。它在医学诊断、模式识别、视频监控、生物鉴别、高清晰电视成像、遥感图像解译、高空对地观测等领域有着广泛的应用。
现有的图像超分辨技术大体可分为3类:基于插值的方法、基于重构的方法和基于学习的方法。
基于插值的方法[1]是图像超分辨技术早期研究的一类主要方法,如双线性插值、双三次插值等,它通过设计具有局部平滑性的插值核函数估计高分辨图像网格上的未知像素值,从而达到增加图像分辨率的目的。基于插值的方法优点在于简单、快速,便于实时应用;其缺点在于不能有效恢复低分辨图像中丢失的高频信息,容易导致图像模糊,满足不了实际应用要求。
基于重构的方法[2, 3]是按照图像退化模型,处理来自同一场景但是彼此之间存在亚像素位移的多幅低分辨图像,利用一定的数学理论对退化图像进行反退化,得到超分辨图像。其优点在于可以保持边缘细节以及抑制人工痕迹;缺点在于当放大倍数比较大时,超分辨图像的质量不能令人满意,会出现图像细节信息丢失,边缘模糊等情况。
基于学习的方法[4, 5, 6, 7, 8, 9, 10, 11, 12, 13]借助机器学习,通过学习低分辨与高分辨图像之间的映射关系,预测低分辨图像中丢失的高频细节信息,从而生成超分辨图像。这种方法由于其现有和潜在的诸多优点,近年来受到了专家和学者的广泛关注。Freeman等人[6]使用马尔科夫随机场(MRF)模型,利用图像局部区域的兼容关系来选择合适的高分辨率图像块,继而生成超分辨率图像。其后,Sun等人[12]在Freeman方法的基础上,提出了利用图像的初始简图先验增强图像边缘的方法;Wang等人[13]将全局重构约束与局部块的细节合成方法组合到一个统一的概率框架下,通过退火Gibbs采样算法生成超分辨率图像。但是,这些方法需要一个庞大的训练集合,计算量很大。为了克服这个缺点,Chang等人[4]借鉴流形学习中局部线性嵌入(LLE)的思想,提出了基于邻域嵌入(NE)的图像超分辨方法。该方法基于高低分辨率图像块组成的流形具
有相似局部结构的假设,将低分辨率块使用样本集合中若干最近邻的线性组合来表示,通过计算重建权值,并将权值传递给高分辨率图像块的线性组合,得到待重建的超分辨率图像。这种方法避免了使用大的训练集合,提高了计算效率,但是重建超分辨图像质量出现了边缘模糊、噪声等问题。近年来,越来越多的学者指出在图像中往往包含着大量的冗余信息,图像的一些结构信息会在图像的不同尺度上重复出现,利用这些信息可以对图像进行更加有效地处理,生成超分辨率图像。 Glasner等人[9]在2009年提出了基于单幅图像的超分辨率重建算法,该算法主要利用图像中重复出现的一些结构信息,采用图像金字塔模型构造一组图像,这些不同尺度空间内的图像块之间存在有一定的自相似性,将这种自相似性结合经典的基于重建的方法,实现对图像的超分辨率重建,得到了比较理想的结果。在此基础上,Freedman等人[10]提出了局部自相似性概念,即图像块在不同尺度空间内的一个小范围内具有一定的自相似性,利用这种局部自相似性,建立了不依赖于外界集合的快速图像超分辨率重建算法,超分辨图像质量方面也取得了不错的效果。但是这两种方法都依赖于图像自身具有很强的自相似性前提,当图像本身的自相似性较弱时,生成的超分辨图像会产生边缘模糊、人工痕迹等问题。
本文针对单幅图像超分辨率重建问题,提出了一种新的结合多尺度局部自相似性和邻域嵌入的超分辨率重建方法。首先,使用双三次插值方法将原始图像放大倍;其次,利用提出的图像降质模型,生成原始图像对应的LR图像;再次,利用图像自身的局部自相似性,在原始图像对应的LR图像的一个小窗口内,寻找原始图像块的个相似LR图像块,结合邻域嵌入方法,计算其重建系数,继而将此重建系数传递给个对应原始图像中的图像块,计算出重建图像块。重复这个过程,直至达到需要的放大倍数。
1 基于多尺度局部自相似性的超分辨自类推方法 1.1 基本思想图像的局部自相似性是指在同一幅图像中存在相同尺度或不同尺度的相似结构,其具体表现为图像中相同尺度或不同尺度中位于局部邻域中的相似图像块。图 1说明了利用局部自相似性进行超分辨率重建的方法原理。训练集合包含3幅图像,分别是原始图像I0、原始图像对应的退化图像I′0以及原始图像对应的插值放大图像H′0。我们的目标是不依赖于任何外界图像,利用图像在不同尺度间的自相似性特征,生成超分辨率图像H0。对于H′0中的图像块p,在I′0对应位置的一个窗口(灰色区域)内,通过某种特征,找到与其相似的图像块p′,在原始图像I0中寻找与p′具有相同位置坐标的图像块q,并将此图像块作为LR图像块p的HR输出,放置在SR图像相应的位置中。按照光栅扫描顺序,对于H′0中的每一个图像块执行此步骤,为了避免人工痕迹,图像块采取有重叠划分,最终得到输出图像H0。

|
| 图 1 基于局部自相似性的超分辨算法基本思想 |
很多方法使用插值方法生成放大的LR图像,借助于外界图像来预测缺失的高频信息。我们同样使用插值方法对原始图像进行放大,本文中使用的滤波器J为双三次插值滤波器,则H′0=J(I0)↑α。
为了预测LR图像H′0中缺失的高频信息,我们需要建立HR-LR图像对,通过图像对之间的对应关系,给出HR图像H0。对于H′0中的每一个子块p,需要在I0的退化图像I′0中寻找与其相似的子块p′,这就要求I′0应该和H′0具有相似的退化效果。为了达到这个效果,我们先将原始图像I0下采样,下采样倍率为1/α倍,再将下采样图像利用双三次插值算法放大α倍,即


这样,我们就得到了原始图像I0所对应的退化图像I′0,以及I0的插值放大图像H′0,通过学习H′0与I′0之间的关系,将I0中的高频信息添加给H′0,获得输出图像H0。
1.3 邻域嵌入算法进行超分辨率增强邻域嵌入(NE)超分辨方法假设LR图像块与对应的HR图像块构成的2个流形在局部几何结构上是相似的。根据该假设,本文使用邻域嵌入流形学习的思想增强 HR图像合成的效果。
令LR图像I′0的子块特征构成的训练集为Xs={xsi}i=1m,HR图像I0的子块特征构成的训练集为Ys={ysi}i=1m,LR图像H′0的子块特征构成的测试集Xt={xtj}j=1m,邻域个数为k。首先从Xs={xsi}i=1m中的子集中查找与xtj最近的k-近邻样本,对应位置构成最近邻集合N(j)。然后计算重构权值wip,使得重构误差最小,重构误差表示如下:


为了保证输出图像H0的空间连续性,我们对H′0中的子块采取了有重叠划分。当所有的HR图像块生成之后,通过融合{ytj}中所有HR图像块,相邻子块的重叠部分取特征的算术平均值,最终获得HR图像H0。
1.4 多尺度框架下超分辨率算法设α为每一次迭代时的尺度因子,M为最终要达到的放大倍数。要达到放大倍数M,需要迭代[lnM/lnα]次。当α选取过小,迭代次数过多,算法的时间复杂度会受到很大影响;当α逐渐增大时,寻找出的匹配子块相似度会下降很快。为此,我们设计了一个实验,来说明尺度因子α取不同值时,局部自相似性的效果。其中,子块大小为3×3个像素,子窗口大小为7×7个像素,特征为RGB空间灰度值(0~255)。图 2给出位于H′0中的所有子块与I′相对应子窗口中最相似子块L1距离的平均值。

|
| 图 2 放大因子取不同值时,子块的平均L1距离 |
从图 2中可以很明显看出,当尺度因子α逐渐增大时,误差也会越来越大。假设我们最终的放大倍数为4倍,如果我们取α为1.05时,则需要迭代29次,这显然太费时;如果我们取α为1.25,则只需迭代7次。在本文的实验结果中,我们最终选取α的值为1.25。
1.5 算法实现令子块大小为n×n个像素,搜索子窗口大小为m×m个像素,子块重叠区域宽度为c个像素,相似子块个数为k,尺度因子为α,最终放大倍数为M,迭代次数为t=[lnM/lnα],LR图像H′0的子块特征构成的测试集Xt={xtj}j=1w,LR图像I′0的子块特征构成的训练集为Xs={xsi}i=1h,HR图像I0的子块特征构成的训练集为Ys={ysi}i=1h。则本文算法叙述如下:
算法:基于局部自相似性和邻域嵌入的超分辨率算法
目标:估计HR图像Ht。
1) 计算I0所对应的退化图像I′0,以及I0的双三次插值放大图像H′0;
2) 将H′0有重叠划分成n×n的子块,重叠区域宽度为c个像素,构成测试集合Xt={xtj}j=1w;
3) 按照光栅扫描顺序,在训练集Xs={xsi}i=1h对应的子集中,计算Xs中的每个样本xtj与Xs={xsi}i=1h中所有样本的距离,查找距离最近的k-近邻,得到邻域集N(j);
4) 计算重构权值wjp,使得重构误差最小化:
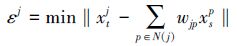
5) 线性组合k-近邻对应的HR图像块,得到HR图像块的估计,即:
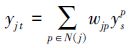
6) 合并所有的HR图像块Yt={ytj}j=1h,生成HR图像H0,相邻图像块重叠区域的像素值使用平均融合得到最终估计值。
7) 令I1=H0,返回步骤1),直至得到最终放大倍数M。
1.6 时间复杂度分析在本文算法中,不依赖于外界图像,在输入图像的不同尺度上使用局部自相似性,迭代生成输出 HR图像。在迭代过程中,我们的算法消耗主要在3个部分:①搜索每一个LR子块所对应的相似结构块;②计算重构权值;③逐层迭代最终得到输出图像。
搜索子块的时间复杂度主要取决于2个因素:搜索子窗口大小m×m和子块大小n×n。假设每一个子块需要和N个子块计算相似性距离,则P=(m-n+1)2,因此,每一个子块的搜索过程需要的时间消耗为O(P)。
计算重构权值的时间复杂度主要取决于2个因素:子块大小n×n;相似子块个数为k。则此阶段需要的时间消耗为O(nk3)。
迭代过程的时间复杂度主要取决于4个因素:输入图像的大小h×w;最终的放大倍数M;尺度因子α;子块大小n×n;重叠区域宽度c。令t为迭代次数,前面已经给出t=[lnM/lnα]。令N为计算过程中需要学习的所有LR子块的个数,则
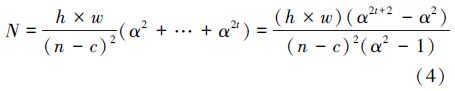
迭代过程需要的时间消耗为O(N)。
综上,本文算法需要的时间复杂度为O(PN+nk3N)。对于1幅128×128的图像,放大3倍,在处理器为Inter Core i5,主频为2.40 GHz的电脑上,用MATLAB R2012b运行,消耗时间为358.992 s,约合6 min。
2 实验结果及分析为验证本文提出的算法有效性,我们采用如图 3所示的9幅图像,将其长和宽都缩小为原来的1/3,作为待超分辨的原始图像,再对生成的原始图像进行放大3倍的超分辨放大实验,并与双三次插值、传统的NE方法两种方法进行比较。

|
| 图 3 测试图像 |
由于人类视觉系统对图像亮度成分的敏感性比色度成分的敏感性更高,因此,先将RGB颜色空间的彩色图像转换到NTSC颜色空间,仅仅对亮度分量进行超分辨放大。在实验中,参数值分别取为n=3、c=2、m=7、α=1.25、k=2。
2.1 实验结果对此客观上,本文采用峰值信噪比(PSNR)评价不同算法的性能。表 1是测试图像在3倍放大情况下的客观评价结果。可以看出,本文提出的方法在所有情况下都比其他2种方法获得的结果要好。
为进一步评价不同算法超分辨性能,图 4比较了Parents图像分别使用3种不同算法重建的结果。可以看出,双三次插值法不能有效恢复图像的高频信息,生成的图像十分模糊。与双三次插值结果相比较,传统的NE方法通过学习HR与LR图像间的对应关系,在一定程度上能有效恢复出LR图像中丢失的高频细节,得到的结果比较清晰。从视觉质量上看,传统的NE方法能够得到比双三次插值方法更多的高频细节,但由于重建过程直接使用1次放大到需要的倍数,得到的图像在纹理细节区域仍出现明显的失真。与上述2种方法得到的结果相比,本文提出的基于邻域嵌入的超分辨自类推方法在保持图像边缘和恢复纹理细节方面都有不同程度的改善,得到的结果不仅边缘更清晰更真实,而且纹理更加丰富。这是由于图像的局部自相似特性在小的尺度因子范围下可以保持良好的特性,在邻域选择过程中,结合局部自相似特性,使得参与重建的图像块均与目标图像块具有相似的结构,因而能获得较好的重建质量。

|
| 图 4 Parents图像结果比较 |
本文针对基于图像自相似性的超分辨算法中存在的不足,提出了一种基于邻域嵌入的快速超分辨自类推方法。首先,提出一种图像退化模型,在此基础上生成不依赖于外界图像的训练集合;其次,在一个小的局部窗口内寻找LR子块的相似图像子块;再次结合邻域嵌入方法,计算重构权值,输出对应的HR图像子块;然后融合所有HR子块,得到本层的HR图像;在多尺度框架内多次重复这个过程,得到最终的HR图像。实验结果表明,本文提出的方法与现有算法相比,在保证算法速度的前提下,同时提高了超分辨重建图像的质量。
| [1] | Su D, Willis P. Image Interpolation by Pixel-Level Data-Dependent Triangulation[J]. Comput Graph Forum, 2004, 23(2): 189-202 |
| Click to display the text | |
| [2] | Lin Z C, Shum H Y. Fundamental Limits of Reconstruction-Based Superresolution Algorithms under Local Reanslation[J]. IEEE Trans on PAMI, 2004, 26(1): 83-97 |
| Click to display the text | |
| [3] | Ben-Ezra M, Lin Z C, Wilbum B Penrose. Pixels: Super-Resolution in the Detector Layout Domain[C]//International Conference on Computer Vision, 2007: 1-8 |
| [4] | Chang H, Yeung D Y, Xiong Y. Super-Resolution through Neighbor Embedding[C]//Conference on Computer Vision and Pattern Recognition, 2004: 275-282 |
| [5] | Yang J, Wright J, Ma Y, et al. Image Super-Resolution as Sparse Representation of Raw Image Patches[C]//Conference on Computer Vision and Pattern Recognition, 2008: 1-8 |
| [6] | Freeman W T. Jones T R, Pasztor E C. Example-Based Super-Resolution[J]. IEEE Computer Graphics and Applications, 2002, 22(2): 56-65 |
| Click to display the text | |
| [7] | Tang Y, Yuan Y, Yan P, et al. Greedy Regression in Sparse Coding Space for Single-Image Super-Resolution[J]. Journal of Visual Communication and Image Representation, 2013, 24(2): 148-159 |
| Click to display the text | |
| [8] | Kim K, Kwon Y. Example-Based Learning for Single-Image Super-Resolution[J]. Pattern Recognition, Lecture Notes in Computer Science, 2008, 5096: 456-465 |
| Click to display the text | |
| [9] | Glasner D, Bagon S, Irani M. Super-Resolution from a Single Image[C]//International Conference on Computer Vision, 2009: 349-356 |
| [10] | Freedman G, Fattal R. Image and Video Upscaling from Local Self-Examples[J]. ACM Transa on Graphics, 2011, 30(2): 60-65 |
| Click to display the text | |
| [11] | Li J, Qu Y, Li C, et al. Learning Local Gaussian Process Regression for Image Super-Resolution[J]. Neurocomputing, 2015, 154: 284-295 |
| Click to display the text | |
| [12] | Sun J, Zheng N, Tao H, et al. Shum. Image Hallucination with Primal Sketch Priors[C]//Proc IEEE Conference on Computer Vision and Patter Recognition, 2003: 729-736 |
| [13] | Wang Q, Tang X, Shum H. Patch Based Blind Image Super Resolution[C]//Proc IEEE International Conference on Computer Vision, 2005: 709-716 |


