有限元法在解决工程问题中发挥着越来越重要的作用,随着其应用的深入,对基于变分原理的有限元法的发展始终没有停止过。在有限元法中,由于单元的位移多项式插值函数在描述几何、材料等不连续性上的不足,仅要求有限元网格能够描述区域的几何特征、材料变化等,只有足够细的网格才能达到所需的精度,这在很大程度上限制了有限元法的应用。为了解决有限元法在处理不连续性上的不足,人们发展了一些新的有限元法,其中基于单位分解法的广义有限元法(GFEM)和扩展有限元法(XFEM)最具代表性,它们都是在有限元法思想上的延伸。GFEM通过在结点处引入广义自由度,对结点进行再次插值,从而提高数值逼近精度,满足对特定问题的特殊逼近要求[1, 2, 3, 4, 5, 6]。广义自由度的物理意义可以理解为以该结点为中心的支集上的局部逼近函数的权重。XFEM通过改进单元的位移形状函数使之包含问题不连续性的基本成分,从而放松对网格密度的过分要求。XFEM附加的自由度的物理意义为结点增强基函数的权重。XFEM在处理诸如模拟界面、裂纹及其扩展、复杂流体等不连续问题时特别有效[7, 8, 9, 10]。GFEM和XFEM在划分用于插值逼近的有限元法网格时,都不需要考虑区域的内部结构细节。
文献[11]结合扩展有限元法和广义有限元法的特点提出了广义扩展有限元法(GXFEM),并用于裂纹扩展分析。在相同网格密度下,GXFEM较XFEM的计算精度高。但是该文的GXFEM继承了XFEM的缺点,混合单元对解的收敛性有影响,而且对结点位移插值函数的形式没有进一步探讨。
本文选用Westergaard裂纹尖端奇异场的基函数作为结点位移插值函数,对裂纹扩展问题的刚度矩阵重新分析,采用Cholesky准则计算刚度矩阵,减少了运算时间。编写了GXFEM裂纹扩展分析程序,通过对典型含裂纹板的数值分析,表明了本文建立的GXFEM在裂纹扩展分析时的有效性和高的计算精度,且Westergaard裂纹尖端奇异场的基函数作为结点位移插值函数较常规的1阶结点位移插值函数精度高。
1 GXFEM的基本原理 1.1 不连续的位移场广义扩展有限元法的基本的思想就是通过增加插值函数的阶次提高计算精度并在单位分解的基础上通过增加描述不连续性的附加函数,模拟裂纹的不连续性及裂纹尖端的奇异性,避免有限元法分析不连续问题时重新划分网格的缺点。为此,构造广义扩展有限元法的位移模式如下:
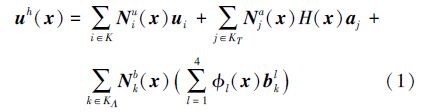
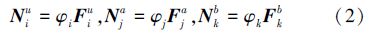
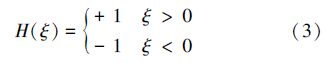
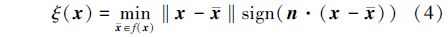

富集单元的结点位移并不是真实的结点位移,为了使所有的结点都是真实的结点位移,需要对(1)式进行转基处理,变换如下:
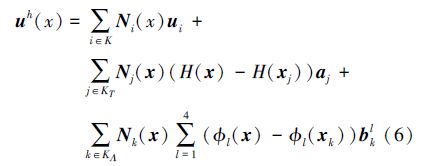
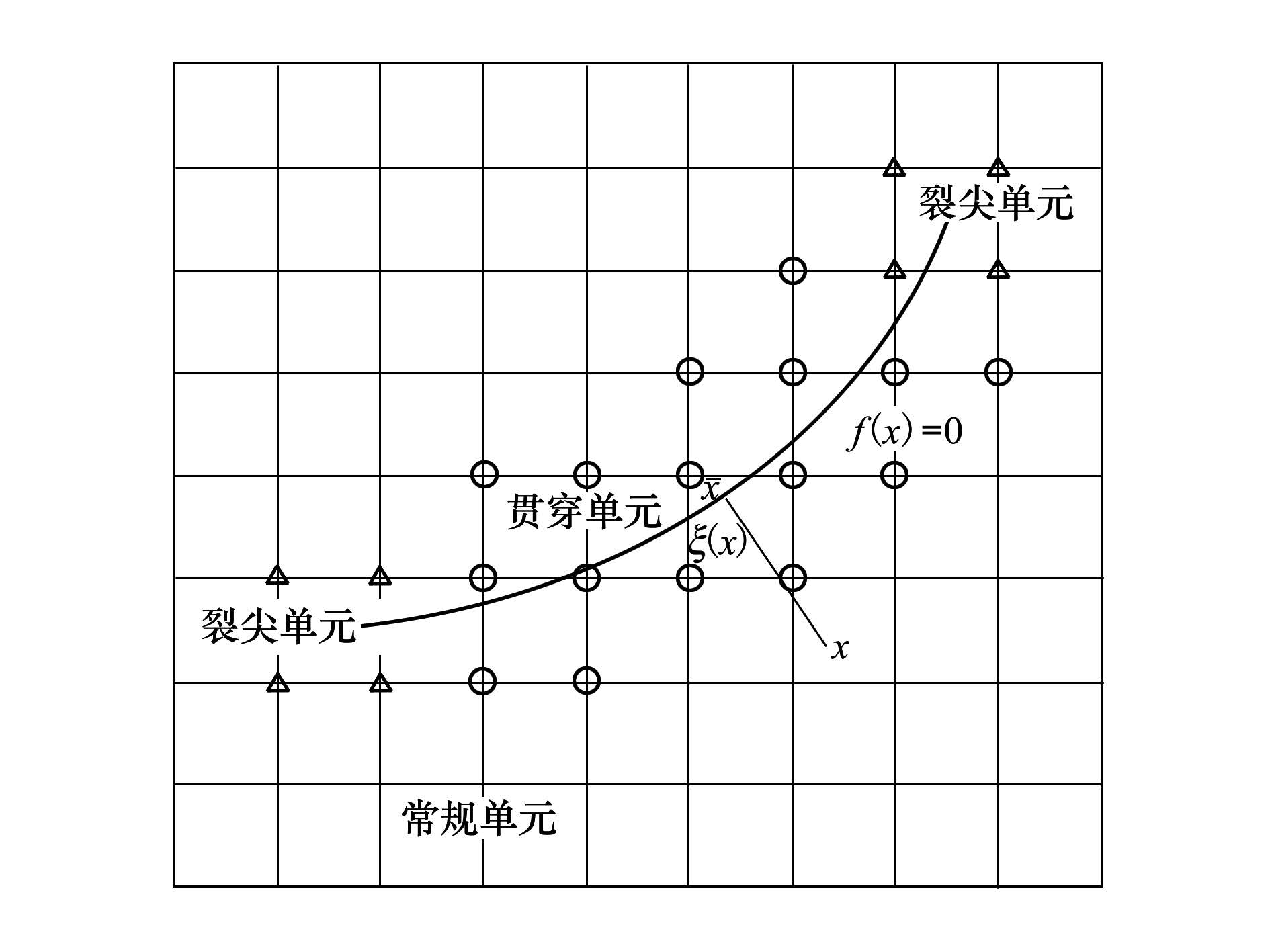
当结点为常规单元的结点时,只有第1项;当结点为被裂纹贯穿单元的结点时,有第1项和第2项;当结点为裂纹尖端所在单元的结点时,有第1项和第3项;结点同时处于裂纹贯穿单元和裂纹尖端所在单元,应优先属于裂纹尖端所在单元,加强方式选择裂纹尖端所在单元结点加强方式,如图 1所示。
|
| 图 1 裂纹的加强结点 |
位移模式可表示为:
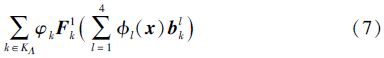
式中,常规单元的结点位移插值函数和裂纹贯穿单元的结点位移插值函数为0阶:
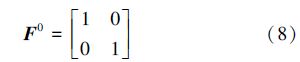
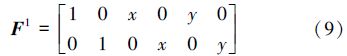
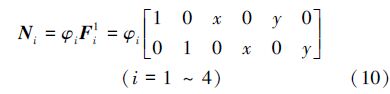
对于裂纹问题,裂纹尖端附近的渐进位移场通常可以运用Westergaard裂纹尖端奇异场:
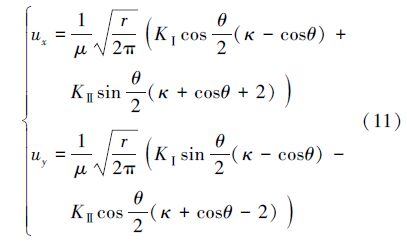
将Westergaard裂纹尖端奇异场的基函数作为结点位移插值函数,得到F为:
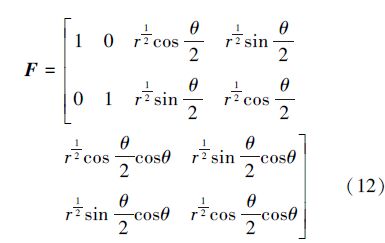
将广义扩展有限元法的位移模式代入弹性体虚功方程,经过变分运算,可得到离散的线性方程组为:

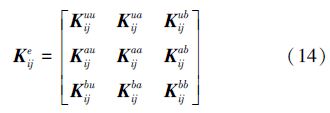

单元荷载列阵f:
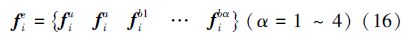
单元荷载力矢量分量表示如下:
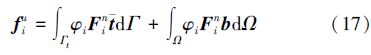
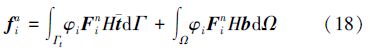
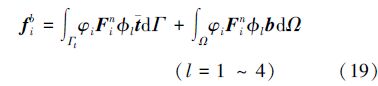
常规应变矩阵:

裂纹贯穿单元附加应变矩阵:

裂纹尖端单元附加应变矩阵:

采用J积分计算应力强度因子,传统的J积分形式[12]为:
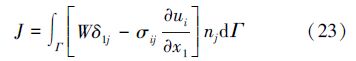
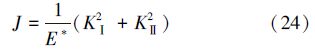
对平面应力问题,E*=E,对于平面应变问题E*=E/(1-μ2)。本文通过在J积分中引入辅助场后推导出相互作用积分来计算应力强度因子。
本文应用最大周向拉应力准则,确定裂纹尖端扩展方向θc:
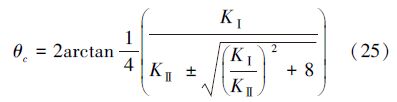
(14)式也可以写成

刚度矩阵中Kijuu是常规有限元法的近似,在裂纹扩展的每个积分里是不会发生改变。这样意味着只有裂纹加强部分的刚度矩阵是改变的,但是改变的部分相对不改变的部分是很小,对于裂纹贯穿单元的仅仅是确定裂纹的位置,刚度矩阵的值在积分里是不会发生改变的。在积分里发生改变的是裂纹尖端所在的单元。为了节省计算时间,我们采用Cholesky准则计算刚度矩阵。这个准则基于裂纹存在于相对小的区域里,也就是加强的单元比较小,而很大的区域是不变的。
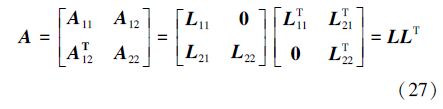
从(26)、(27)式可以得到:
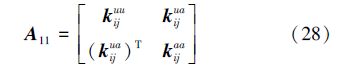

在有裂纹这种强不连续存在时,扩展有限元单元不需要重新划分网格,广义扩展有限元也有这样的特点。广义扩展有限元进行单元分解的目的是数值积分。在裂纹经过单元采用和常规有限元相同数目的积分显然是不能达到要求的。为了保证积分的精度,采用以下的积分方案:
如图 2所示,对于传统四结点等参单元的单元劲度矩阵即没有结点加强的单元,其积分方案采用2×2个高斯积分点。由于阶次的提高(较传统四结点等参单元被积函数阶次至少要高一次),对广义扩展有限元四结点等参单元计算单元劲度矩阵宜采用9个高斯积分点。
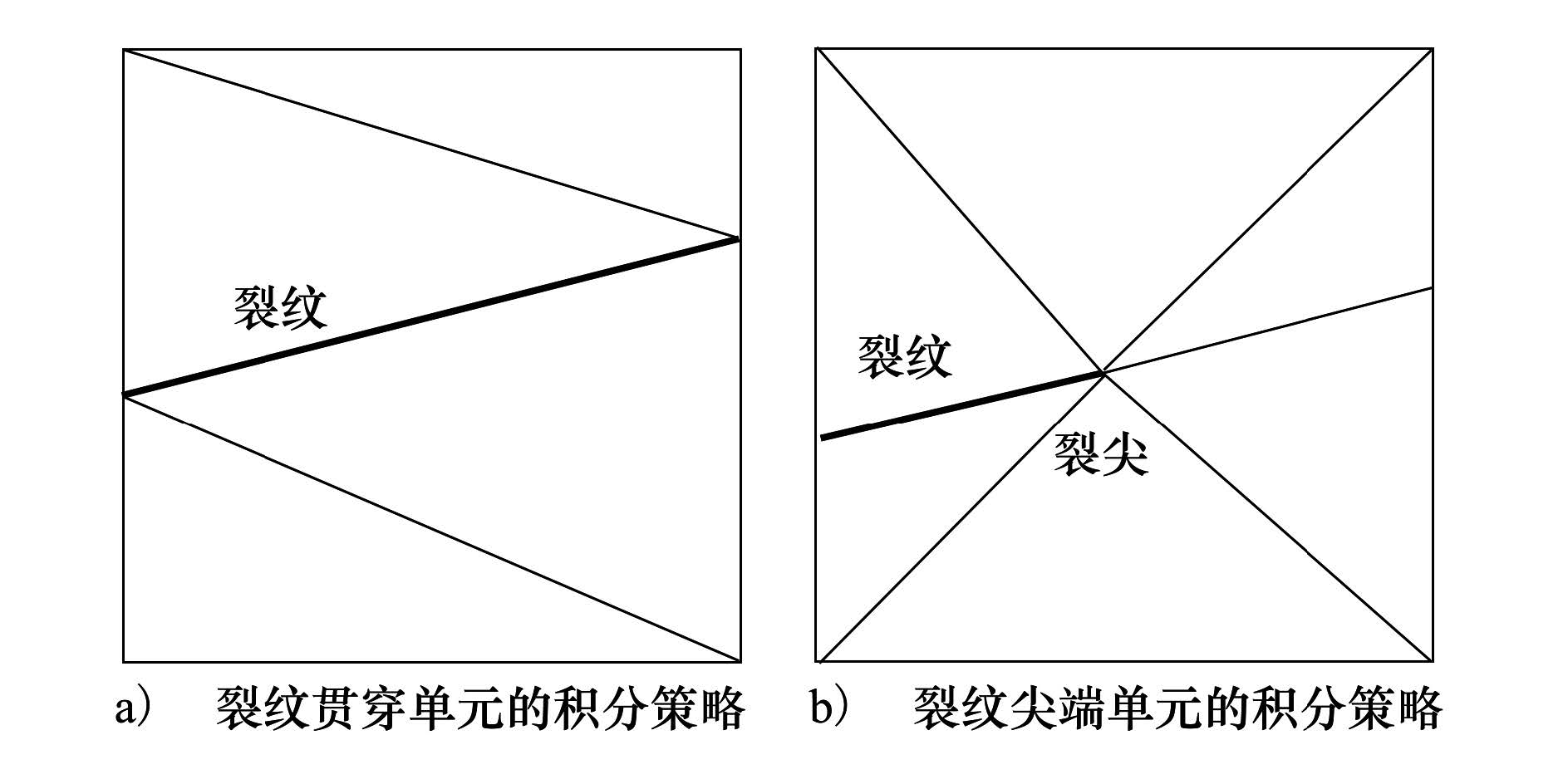
|
| 图 2 单元的分块积分策略 |
没有裂纹穿过,但有结点加强的单元,采用6×6个高斯积分点。
若4个结点都是Heaviside加强,在裂纹贯穿单元,裂纹将单元分为2个子域,分别由每个子域的角点形成Delaunay三角形,每个三角形内采用3×3个高斯积分点。
在裂纹尖端单元,缝尖延长,将单元分成两个子域,分别由每个子域的角点形成Delaunay三角形,每个三角形内采用9×9个高斯点积分。在积分时将积分区分为这些三角形,并不增加整体的自由度数,只是积分的需要。
3.2 广义扩展有限元与有限元的联合运用为了解决实际问题的计算效率和精度这一问题,可针对具体实际问题的结构形式或所关心问题的区域,将广义扩展有限元与扩展有限元联合运用。因为广义扩展有限元兼具广义有限元和扩展有限元的特点,因此广义扩展有限元中结点位移的插值多项式阶次可以按照需要任意选取,而不影响位移的协调性问题,对广义扩展有限元的常规四结点单元中按照1阶的结点位移插值函数建立的程序,每个结点有6个广义位移(自由度),只要将某些结点后4个自由度施加约束,那么就自然退化成传统有限元的结点位移,因此只要对约束信息做恰当的处理,无需修改程序就可以实现广义扩展有限元与扩展有限元的联合运用。因为广义有限元中结点的自由度为广义位移,故在求得结点广义位移后,还需要通过结点的位移插值函数求的结点最终位移值。
3.3 广义扩展有限元线性相关性的处理由于广义扩展有限元的局部逼近函数大多存在线性相关性,广义扩展有限元方法的刚度矩阵如广义有限元的刚度矩阵一般具有奇异性。广义扩展有限元方法中,零特征根的个数一般不知道。因此需要求解以半正定矩阵A为系数的线性方程组即Ac=b,文献[15]提出了解决方法。
4 数值算例 4.1 单边裂纹平板受单向均匀拉伸长度为a的单边裂纹平板如图 3所示。

|
| 图 3 单边裂纹平板受拉伸 |
L=6 m,W=3 m,受单向均布拉应力σ=1 MPa,板的弹性模量E=10 MPa,泊松比为0.3。文献[16]给出了该问题的应力强度因子(SIF)的经验公式。有限元网格密度为15×31,采用不同方法计算得到的应力强度因子列于表 1。
从表 1的计算结果可以看出,GXFEM较XF-EM的计算结果更接近解析解,且使用(12)式的结点位移插值函数的计算结果较(9)式作为结点位移插值函数更接近解析解。
| 裂纹长度a/m | 应力强度因子(SIF)/(MPa·(m)-1/2) | 相对误差/% | ||||||
| XFEM | GXFEM(9)式 | GXFEM(12)式 | 文献[16] | XFEM | GXFEM(9)式 | GXFEM(12)式 | ||
| 0.6 | 1.804 8 | 1.842 8 | 1.879 0 | 1.882 1 | -4.107 1 | -2.088 1 | -0.164 7 | |
| 0.8 | 2.359 7 | 2.403 2 | 2.452 3 | 2.458 4 | -4.014 8 | -2.245 4 | -0.248 1 | |
| 1.0 | 3.044 3 | 3.105 7 | 3.176 6 | 3.166 1 | -3.847 0 | -1.907 7 | 0.331 6 | |
| 1.2 | 3.919 3 | 4.023 2 | 4.114 4 | 4.085 0 | -4.056 3 | -1.512 9 | 0.719 7 | |
如图 4所示,一矩形板内含有一条中心斜裂纹,矩形板的上端和下端受到竖直方向的单向拉伸载荷σ=1 MPa,矩形板的高和宽为W=10 m,裂纹长度为2a=1 m。材料弹性模量为E=71.7 GPa,泊松比为μ=0.33。该模型的应力强度因子解析解取自文献[16]。

|
| 图 4 中心斜裂纹板 |
选取网格密度为100×101。采用不同方法计算得到的应力强度因子KⅠ和KⅡ随裂纹角的变化曲线如图 5所示。
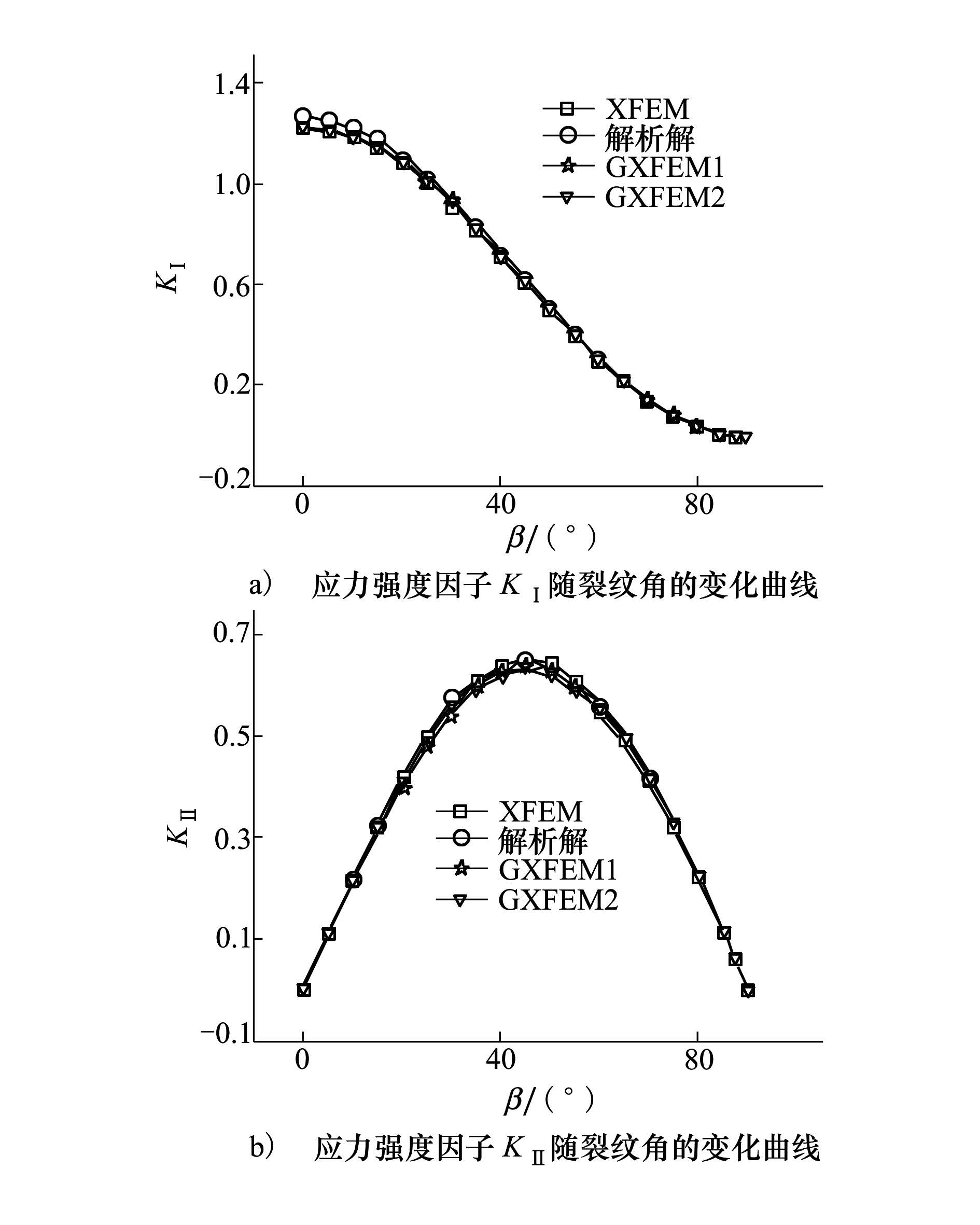
|
| 图 5 应力强度因子随裂纹角的变化曲线 |
从图 5可以看出,GXFEM比XFEM计算结果更接近解析解。但是因为网格密度较密,各种方法的精度差距不大,GXFEM的优势主要体现在网格密度不大的时候,仍能精确的得到应力强度因子,而且本例是单向拉伸,高阶位移插值函数的效果有限。
选取半裂纹长度0.5m,角度为30°,应用广义扩展有限元模拟裂纹扩展。分别采用4种网格密度,网格1为50×51,网格2为80×81,网格3为100×101,网格4为120×121,图 6给出了不同网格对应的裂纹扩展路径。

|
| 图 6 不同网格对应的裂纹扩展路径 |
从图 6可以看出,随着网格密度的增加,裂纹扩展的路径几乎重合,表明当网格密度增加到一定程度时,可以很好的模拟裂纹扩展。
5 结 论从广义扩展有限元的位移场构造和验证算例两方面可以看出,广义扩展有限元法的精确明显高于扩展有限元法,而且选用Westergaard裂尖奇异场的基函数作为结点位移插值函数(即(12)式)比采用一阶结点位移插值函数(即(9)式)的精度要高。广义扩展有限元结点位移插值多项式可以任意选取,且不影响位移的协调性问题,其继承了广义有限元的优点,但是对于其刚度奇异性问题还需要做更进一步的研究。
广义扩展有限元可以退化为扩展有限元、广义有限元甚至常规有限元。在考虑不连续问题时,只需要对不连续的区域进行结点自由度的广义化和增加富集函数,对于其他的区域可以采用常规有限元。
| [1] | Babushka I, Osborn. Generalized Finite Element Methods: Their Performance and Their Relation to Mixed Methods[J]. SIAM Journal of Numerical Analysis, 1983, 20(3): 510-535 |
| Click to display the text | |
| [2] | Duarte C A, Babuska I, Oden J T. Generalized Finite Element Methods for Three-Dimensional Structural Mechanics Problems[J]. Computer & Structures, 2000, 77: 215-232 |
| Click to display the text | |
| [3] | Strouboulis T, Copps K, Babuska I. The Generalized Finite Element Method[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190: 4081-4193 |
| Click to display the text | |
| [4] | Strouboulis T, Zhang L, Babuska I. Generalized Finite Element Method Using Mesh-Based Handbooks: Application to Problems in Domains with Many Voids[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(28/29/30): 3109-1361 |
| Click to display the text | |
| [5] | Duarte C A, Babuska I. Mesh-Independent Porthotropic Enrichment Using the Genernalized Finite Element Method [J]. International Journal for Numerical Methods in Engineering, 2001, 55(12): 1477-1492 |
| Click to display the text | |
| [6] | Babuska I, Banerjee U, Osborn J E. Survey of Meshless and Generalized Finite Element Methods: a Unified Approach[J]. Acta Numerica, 2003, 12:1-125 |
| Click to display the text | |
| [7] | Sukumar N, Chopp D L, Moran B. Extended Finite Element Method and Fast Marching Method for Three-Dimensional Fatigue Crack Propagation[J]. Engineering Fracture Mechanics, 2003, 70: 29-48 |
| Click to display the text | |
| [8] | 陈金龙, 战楠, 张晓川. 基于扩展有限元法的裂尖场精度研究[J]. 计算力学学报, 2014, 31(4): 425-430 Chen Jinlong, Zhan Nan, Zhang Xiaochuan. Numerical Study on the Accuracy of Crack Tip Field by Extended Finite Element Method[J]. Chinese Journal of Computational Mechanics, 2014, 31(4): 425-430 (in Chinese) |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 宋娜, 周储伟. 扩展有限元裂尖场精度研究[J]. 计算力学学报, 2009,26(4): 544-547 Song Na, Zhou Chuwei. Accuracy Study of Crack Tip Field in Extended Finite Element Method[J]. Chinese Journal of Computational Mechanics, 2009, 26(4): 544-547 (in Chinese) |
| Cited By in Cnki (11) | Click to display the text | |
| [10] | Tarancon J E, Vercher A, Giner E. Enhanced Blending Elements for XFEM Applied to Linear Elastic Fracture Mechanics[J]. International Journal for Numerical Methods in Engineering, 2009, 77(1):126-148 |
| Click to display the text | |
| [11] | Zhang Qing, Liu Kuan, Xia Xiaozhou, Yang Jing. Generalized Extended Finite Element Method and Its Application in Crack Growth Analysis[J]. Chinese Journal of Computational Mechanics, 2012, 29(3): 427-432 |
| [12] | Moran B, Shih C F. Crack Tip and Associated Domain Integrals from Momentum and Energy Balance[J]. Engineering Fracture Mechanics, 1987, 27(6): 615-642 |
| Click to display the text | |
| [13] | Yau F J, Wang S S, Corten H T. A Mixed-Mode Crack Analysis of Isotropic Solids Using Conservation Laws of Elasticity[J]. Journal of Applied Mechanics, 1980, 47: 335-341 |
| Click to display the text | |
| [14] | Pais M J, Kim N H, Davis T. Reanalysis of the Extended Finite Element Method for Crack Initiation and Propagation[R]. AIAA-2010-2536 |
| [15] | 李录贤,刘书静,张慧华,等. 广义有限元方法研究进展[J]. 应用力学学报, 2009, 26(1): 96-108 Li Luxian, Liu Shujing, Zhang Huihua, et al. Researching Progress of Generalized Finite Element Method[J]. Chinese Journal of Applied Mechanics, 2009, 26(1): 96-108 (in Chinese) |
| Cited By in Cnki (17) | Click to display the text | |
| [16] | 中国航空研究院. 应力强度因子手册[M](增订版). 北京:科学出版社, 1993, 12: 251-252; 348-349 China Aviation Institute. Manual of Stress Intensity Factor[M](Revised Edition). Beijing: Science Press, 1993, 12: 251-252; 348-349 (in Chinese) |


