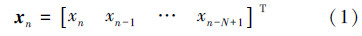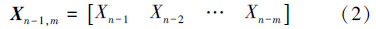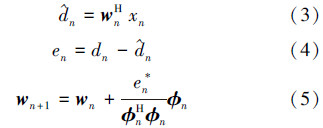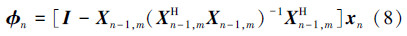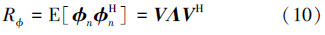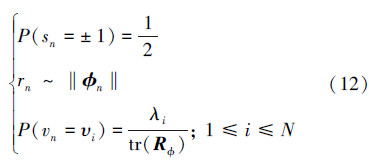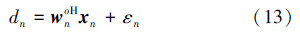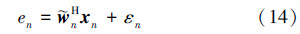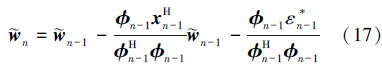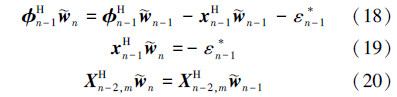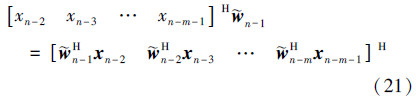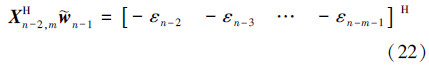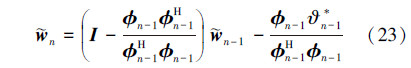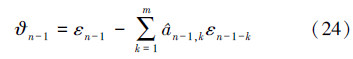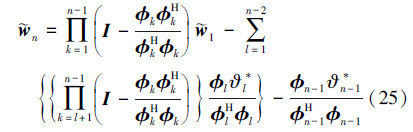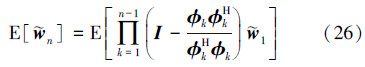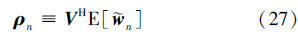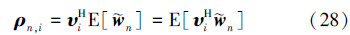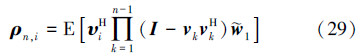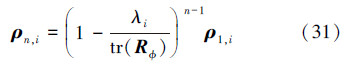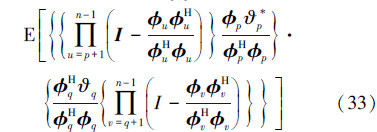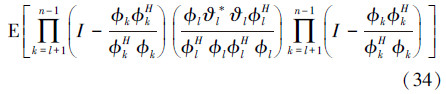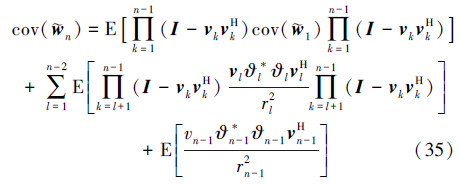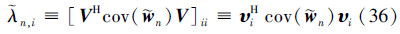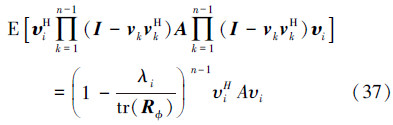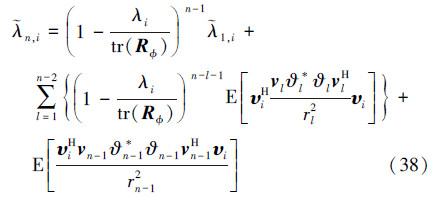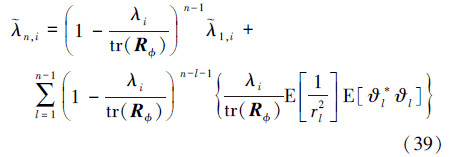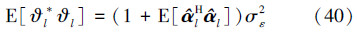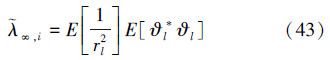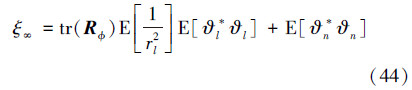2. 温州大学 商学院, 浙江 温州 325035
对于自相关的输入信号，相比较于归一化最小均方算法，仿射投影算法获得了比较快的收敛速度。在针对AP算法的研究中，文献[1]首先基于几何的方法，提出了AP算法。文献[2]通过定义输入信号的方向向量，在参数迭代步长等于1时，分别针对自回归模型、滑动平均模型和自回归滑动平均模型，建立了一种仿射投影算法。在参数迭代步长等于1时，针对自回归模型，文献[3]分析了AP算法收敛性的随机统计模型。接着，在参数迭代步长小于1时，文献[4]分析了AP算法收敛性的随机统计模型，建立了AP算法权值误差和权值均方误差的递归迭代模型。在假定输入信号独立同分布的条件下，文献[5]给出了仿射投影算法的定量分析，建立了其权值误差和权值均方误差的递归迭代模型。在文献[6, 7]中，分析了过去噪声对权重误差的影响，获得了AP算法的统计模型。
在参数迭代步长等于1，不考虑系统测量噪声时，AP算法获得了最快的收敛速度。因此，在参数迭代步长等于1时，本文研究了AP算法收敛性的随机统计模型，建立了其权值误差和权值均方误差的递归迭代模型，获得了AP算法稳定状态的误差。
1 仿射投影算法在自适应滤波器的系统辨识模型中，独立同分布的输入信号可以转换为输入向量xn,其定义为
基于最近过去的输入向量数m,定义输入矩阵Xn-1,m为
文献[1, 2]中定义了仿射投影算法的权值更新方程,其定义如下:
其中输入信号的方向向量φn定义为
根据最小二乘算法,向量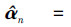 
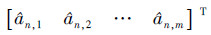的计算如下
从(9)式可以看出,输入信号的方向向量与最近过去的m个输入向量正交。由于AP算法的迭代方向为输入信号的方向向量,因此促进了自适应滤波器的收敛速度。
2 输入信号方向向量的统计特性输入信号的方向向量φn是一个误差向量,它由最小二乘算法利用最近过去的输入向量估计而得。为了便于分析AP算法收敛性的随机统计模型,给出了下面的3个假设条件。
1) 输入信号的方向向量φn与仿射投影算法的权重向量wn相互的独立,其自相关矩阵为
式中,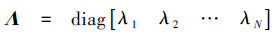
和V=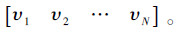 
。后者为相互正交的特征向量,这个假设的合理性在文献[3]中已被证明。
2) 输入信号的方向向量φn由3个独立的随机变量组成,并且独立同分布。即
式中 rn～‖φn‖表示rn与真实输入信号的方向向量具有相同的分布,tr(·)表示求矩阵的迹。在文献[5, 6, 8]中,对输入向量xn做了相似的假设。
3) 假定自适应滤波器存在一个真实的权值向量wno,其实际输出信号可由(13)式计算
式中系统的测量噪声εn是方差等于σε2的高斯白噪声信号,其均值等于0。因此,由(3)式、(4)式和(13)式,可得自适应滤波器的估计输出误差信号 式中 3 平均权值误差
为了分析(5)式的收敛特性,根据(5)式和(14)式,可得
由(15)式和(16)式,可得自适应方程的误差迭代方程为 将(17)式分别左乘以φn-1H、xn-1H和Xn-2,mH,利用(4)式和(9)式,其中xn-1H=φHn-1+Hn-1Xn-2,mH,可得: 由(2)式和(20)式,可得 在(21)式中递归调用(19)式,可得 将(6)式代入(17)式,基于(22)式,得到 式中
基于(23)式递归计算AP算法的权值误差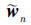 
,可得
基于相互正交的向量｛υ1,υ2,…,υN｝,定义向量ρn为
因此 基于(11)式和(12)式,利用(28)式的结果,将(26)式左乘以向量υHi,可得 由于特征向量υi的正交性,可得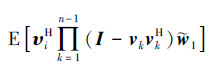
可表示从一系列被标记为1,2,…,N,总计为N的球中进行抓球实验,其值等于标记为i的球在(n-1)次实验中未被抓到的概率相同,其中每次抓到标记为i的球的概率为λi／tr(Rφ),所以(23)式可写为
4 权值均方误差
根据(25)式,AP算法权值误差的协方差矩阵可写为
由于系统的测量噪声εl是均值等于零的高斯白噪声信号,因此(32)式中第2~5项都等于0。同时,在假设A1和A2的条件下,E[φHkφl]=E[φHk]E[φl],k≠l且E[slrlvl]=E[sl]E[rl]E[vl]=0。因此,可知(32)中第7、8项变为0。(32)式中第6项可以认为是维数(n-2)×(n-2)矩阵M的所有元素之和,M的元素mp,q为
在这3个假设的条件下,当p<q时,φp与其他输入信号的方向向量相互独立;当q<p时,φq与其他输入信号的方向向量相互独立,且输入信号的方向向量φp和φq的均值为0。因此,可知矩阵M的非对角线元素为0。由于系统的测量噪声εl是均值等于0的白噪声信号,可得矩阵M的对角线元素ml,l为
基于(34)式,将(11)式代入(32)式,可得
定义协方差矩阵的对角线元素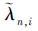 
为
在假设A2和A3的条件下,可知vl为υi的概率是λi／tr(Rφ)。利用(30)式、(38)式可以写为
由于系统的测量噪声是均值等于零的白噪声,利用(24)式,可知(39)式中的E[ϑl*ϑl]可以写为
将(6)式带入(14)式,根据(22)式和(24)式,估计的误差信号en可写为
由于系统的测量噪声εn是均值等于零的白噪声信号,根据(36)式和(41)式,在假设A1的条件下,仿射投影算法的均方误差可以被写成
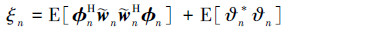
假设AP算法收敛,随着自适应滤波器的迭代次数n→∞,(33)式中的第1项趋近于0,第2项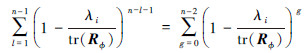 
是一个几何序列。因此,当n→∞,(39)式可写为
在不考虑系统测量噪声的条件下，参数迭代步长等于1时，AP算法获得了最快的收敛速度。在此条件下，本文研究了AP算法收敛性的随机统计模型，建立了AP算法的权值平均误差和权值均方误差的递归迭代方程，获得了AP算法均方误差的统计模型。最后分析了AP算法均方误差的稳定状态。
| [1] | Ozeki K, Umeda T. An Adaptive Filtering Algorithm Using an Orthogonal Projection to an Affine Subspace and Its Properties[J]. Electronics and Communications in Japan, 1984, 67(5): 19-27 |
| Click to display the text | |
| [2] | Pupp M. A Family of Adaptive Filter Algorithms with Decorrelating Properties[J]. IEEE Trans on Signal Process, 1998, 46(3): 771-775 |
| Click to display the text | |
| [3] | Sjmd Almeida, Jcm Bermudez, Nj Bershad. A Statistical Analysis of the Affine Projection Algorithm for Unity Step Size and Autoregressive Inputs[J]. IEEE Trans on Circuits Syst I——Fundam Theory Appl, 2005, 52(7): 1394-1405 |
| Click to display the text | |
| [4] | Sjmd Almeida, Jcm Bermudez, Nj Bershad. A Stochastic Model for a Pseudo Affine Projection Algorithm[J]. IEEE Trans on Signal Process. 2009, 57(1): 107-118 |
| Click to display the text | |
| [5] | Sankaran S G, Beex A A. Convergence Behavior of Affine Projection Algorithms[J]. IEEE Trans on Signal Process, 2000, 48(4): 1086-1096 |
| Click to display the text | |
| [6] | Tk Paul, Ogunfunmi T. On the Convergence Behavior of the Affine Projection Algorithm for Adaptive Filters[J]. IEEE Trans on Circuits Syst I——Fundam Theory Appl, 2011, 58(8): 1813-1826 |
| Click to display the text | |
| [7] | Se Kim, Jw Lee, Wj Song, A Theory on the Convergence Behavior of the Affine Projection Algorithm[J]. IEEE Trans on Signal Process, 2011, 59(12): 6233-6239 |
| Click to display the text | |
| [8] | Dtm Slock. On the Convergence Behavior of the LMS and the Normalized LMS Algorithms[J]. IEEE Trans on Signal Process, 1993, 41(9): 2811-2825 |
| Click to display the text |
2. School of Business, Wenzhou University, Wenzhou 325035, China