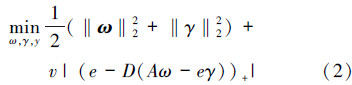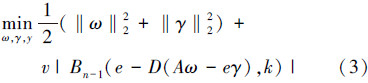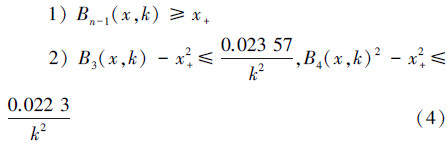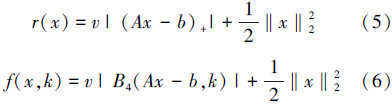基于统计学习理论的支持向量SVM(support vector machine)比其他方法有更好的分类性能和效率,并且它已成功应用于模式识别和回归问题[1, 2, 3, 4]。基于支持向量机的这些优点,许多研究者致力于SVM的研究并取得了很大的进步。2001年,由Lee等人针对数学规划问题中的不光滑问题提出Sigmod光滑函数[5]。2005年,袁玉波等人也提出了2个多项式光滑函数[6]得到了PSSVM模型。2007年袁玉波等人又提出了三次样条插值函数得到了TSSVM模型[10]。由于它们对加号函数的逼近性能还有待提高。因此本文提出了贝塞尔光滑模型,理论分析和数值实验都证明它在数据分类的性能和效率上优于TSSVM和PSSVM模型。
1 贝塞尔光滑支持向量机模型 1.1 贝塞尔函数贝塞尔曲线是通过插值的方法获得的。给定点p0,p1,p2,…,pn-1,则贝塞尔曲线为
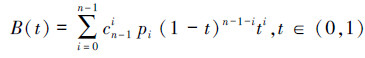
 ,0),pi=(0,0),(i=1,2,3,…,n-2),pn-1=(
,0),pi=(0,0),(i=1,2,3,…,n-2),pn-1=( ,
, ),则贝塞尔曲线变为B(t)=p0(1-t)n-1+pn-1tn-1,t∈[0, 1],将p0,p1,p2,…,pn-1代入B(t)中得到Bx(t)=-
),则贝塞尔曲线变为B(t)=p0(1-t)n-1+pn-1tn-1,t∈[0, 1],将p0,p1,p2,…,pn-1代入B(t)中得到Bx(t)=- (1-t)n-1+
(1-t)n-1+ tn-1,t∈(0,1),By(t)=
tn-1,t∈(0,1),By(t)= tn-1,t∈(0,1),消去t,得到贝塞尔函数公式B(x,k)。显而易见,B(x,k)在x∈(-
tn-1,t∈(0,1),消去t,得到贝塞尔函数公式B(x,k)。显而易见,B(x,k)在x∈(- ,
, )区间单调递增。因此贝塞尔函数存在逆函数[8]。所以在实数空间中我们可以选择用逆函数来替换原函数。
)区间单调递增。因此贝塞尔函数存在逆函数[8]。所以在实数空间中我们可以选择用逆函数来替换原函数。
贝塞尔函数的逆函数推导过程如下:
先给定3个点p0=- ,0,p1=(0,0),p2=(
,0,p1=(0,0),p2=( ,
, ),利用其插值,我们可以得到二次方贝塞尔曲线和它相应的逆函数B2-1 (x,k)=x-
),利用其插值,我们可以得到二次方贝塞尔曲线和它相应的逆函数B2-1 (x,k)=x- 。类似的通过插值4个点p0=(-
。类似的通过插值4个点p0=(- ,0),p1=p2=(0,0),p3=(
,0),p1=p2=(0,0),p3=( ,
, ),得到三次方贝塞尔曲线和其相应的逆函数B3-1 (x,k)=
),得到三次方贝塞尔曲线和其相应的逆函数B3-1 (x,k)=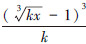 。以此类推,通过插值n个点p0(-
。以此类推,通过插值n个点p0(- ,0),pi=(0,0),(i=1,2,3,…,n-2),pn-1=(
,0),pi=(0,0),(i=1,2,3,…,n-2),pn-1=( ,
, ),得到n-1阶贝塞尔曲线和其相应的逆函数Bn-1-1 (x,k)=x+(-1)n
),得到n-1阶贝塞尔曲线和其相应的逆函数Bn-1-1 (x,k)=x+(-1)n 。
。
考虑如下的分类问题:在n维实空间中将m个点分类,矩阵Am×n的每一行向量代表一个点。如果Ai属于A+,标记为1,如果Ai属于A-,则标记为-1,那么分类情况可以用一个m×m的对角矩阵D来示,其中D的对角线元素为1或-1。则这个问题的标准向量机模型[9]为:对任意v>0
式中,ω是边界面的法向量,γ表示边界面到原点的距离,y是松弛变量。这是一个有约束条件的二次规划问题。修正该模型的目标函数[9],可得到其无约束优化模型: 虽然模型(2)的目标函数具有强凸性和唯一解,但不具有光滑性,不能利用快速算法求解。为了能用 Newton-Armijo快速算法求解,引入光滑技术[5, 6, 10],对上述无约束优化模型进行光滑处理。本文使用n-1阶贝塞尔函数作光滑函数可得到一类贝塞尔光滑支持向量机模型: 2 性能分析 2.1 逼近性能分析当贝塞尔函数的中间控制点xi→0,i=1,2,…,n-2时,根据样条函数的特性,贝塞尔函数和正号函数之间的插值误差将会减小。因此当xi→0,i=1,2,…,n-2时,贝塞尔函数对正号函数的逼近性能优于以往提出的光滑曲线。并且贝塞尔函数的阶数越高,其对加号函数的逼近性能就越好。下面以四阶贝塞尔函数为例,分别从理论分析和实验仿真证明贝塞尔函数性能的优越性。
为便于比较贝塞尔函数与其他光滑函数对正号函数的逼近精度,我们给出如下的定理:
定理1 对于任意k,贝塞尔函数Bn-1(x,k)在插值节点x=± ,x=0关于x具有n-1阶光滑性。
,x=0关于x具有n-1阶光滑性。
证明过程见附录。
定理2 对于x∈Ω,k∈R+,B3(x,k)定义为三阶贝塞尔函数,B4(x,k)定义为四阶贝塞尔函数,x+定义为正号函数,则对于任意的x,k,有下面的结论:
证明过程见附录。
下面对5个光滑函数逼近正号函数的精度进行比较:
1) 文献[5]知,当光滑函数取Sigmoid函数的积分函数[5]时,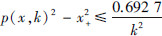
2) 由文献[7]知,当光滑函数取三阶多项式光滑函数式时,
3) 由文献[10]知,当光滑函数取三次样条插值函数式时,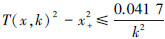
4) 由定理2知,当光滑函数取三阶和四阶贝塞尔函数时,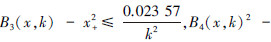

可见,三阶和四阶贝塞尔函数对原函数的逼近性能优于其他3种光滑函数。对上述各个函数在区间-1k,1k对加号函数的逼近程度进行理论仿真,不妨取光滑因子k=10,其仿真结果如图 1所示。从图中看出,三阶和四阶贝塞尔函数的逼近精度优于其他光滑函数。由此可以验证:新模型BSSVM1的求解效果优于其他光滑函数。
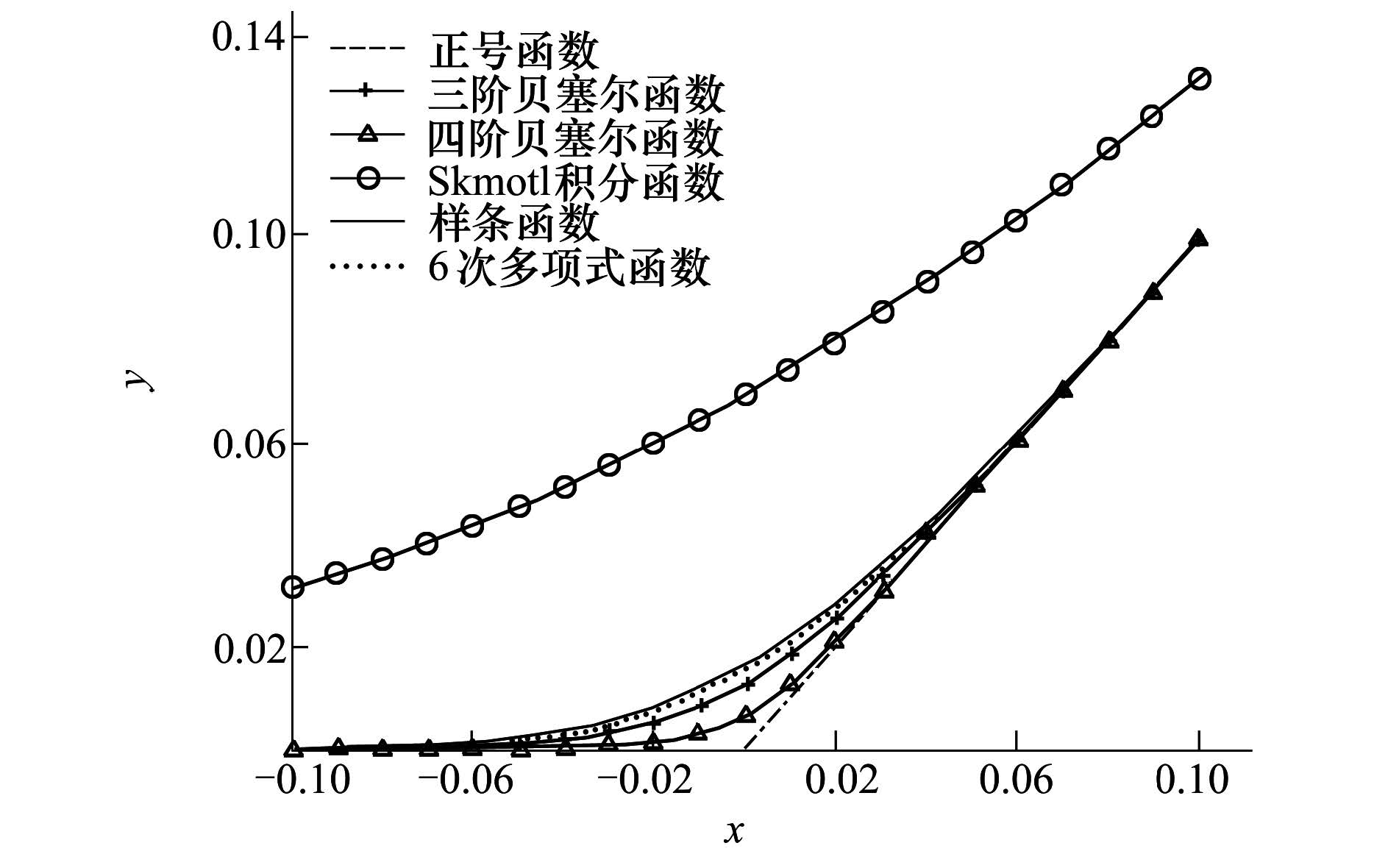 |
| 图 1 k=10时的光滑函数对比图 |
定理3 设A∈Rm×n,b∈Rm×1,实函数r(x):Rn→R和f(x,k):Rn×N→R定义如下:
则有如下结论:
1) r(x),f(x,k)是强凸函数;
2) 优化模型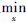 r(x)存在唯一解x*,优化模型
r(x)存在唯一解x*,优化模型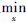 f(x,k)存在唯一解xk*;
f(x,k)存在唯一解xk*;
3)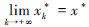
证明:
1) 由‖·‖22的强凸性显然可以证明r(x),f(x,k),是强凸函数。
2) 由于B4(x,k)≥x+,水平集Lv(r(x))和Lv(f(x,k))满足:Lv(f(x,k))⊆Lv(r(x))⊆{x|‖x‖22≤2v}。因此Lv(r(x))和Lv(f(x,k))是紧子集。所以证明2个模型的解存在,又由于2个函数是强凸函数,从而它们的解具有唯一性。
3) 为了证明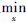 f(x,k)的最优解在k→+∞时收敛于
f(x,k)的最优解在k→+∞时收敛于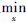 (x)的最优解,由一阶最优化条件和r(x),f(x,k)的强凸性,得
(x)的最优解,由一阶最优化条件和r(x),f(x,k)的强凸性,得
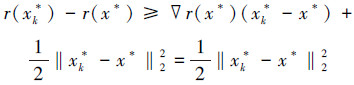
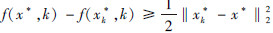 将上面两式相加,并注意到f(x,k)≥x+,有
将上面两式相加,并注意到f(x,k)≥x+,有
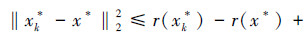

根据定理2结论(2)的推导原理,有|B4(x,k)|-|x+|≤ ,进一步得到‖xk*-x*‖22≤
,进一步得到‖xk*-x*‖22≤ 。当k→+∞时,
。当k→+∞时,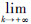 ‖xk*-x*‖22=0。因此,证明了结论。
‖xk*-x*‖22=0。因此,证明了结论。
本文比较4种模型即SSVM、FPSSVM、TSSVM、BSSVM1的计算效率和分类性能。 Newton-Armijo算法[11]是一种求模型(3)最优解的快速算法。比较的数据有计算时间、训练样本正确率测试样本正确率。本实验是基于1.9GHZ AMD APU和4GB RAM 的个人计算机上的MATLAB R2011b平台。实验参数设置为k=10,ε=10-8,并且用十折交叉校验法测试算法的精确度。训练样本(M×N)表示M个N维的样本集。实验结果如表 1和表 2所示。
| 线性数据集 | 算法 | 计算时间/s | 训练样本分类正确率/% | 测试样本分类正确率/% |
| SSL (set=2) 1 500×241 |
SSV MFPSSVM TSSVM BSSVM1 |
0.72 0.58 0.60 0.56 |
96.2 96.37 96.40 96.38 |
91.47 91.53 91.53 91.67 |
| Pima diabetes 768×8 |
SSV MFPSSVM TSSVM BSSVM1 |
0.01 0.01 0.02 0.03 |
77.79 77.79 77.84 78.15 |
77.33 77.33 77.46 77.85 |
| Hepatitis 155×19 |
SSV MFPSSVM TSSVM BSSVM1 |
0.03 0.01 0.02 0.03 |
89.17 89.17 89.10 91.25 |
79.29 79.29 79.29 79.29 |
| Bupa 345×6 |
SSV MFPSSVM TSSVM BSSVM1 |
0.04 0.01 0.06 0.03 |
64.91 69.95 69.98 70.85 |
69.85 64.62% 64.92 65.78 |
| 数据集 (m×n) | 算法 | 计算时间/s | 训练样本分类正确率/% | 测试样本分类正确率/% |
| 1 000×100 | SSVM FPSSVM TSSVM BSSVM1 |
0.19 0.14 0.16 0.17 |
97.40 97.40 97.40 97.80 |
98.00 98.00 98.00 98.00 |
| 10 000×100 | SSVM FPSSVM TSSVM BSSVM1 |
1.35 1.02 1.06 1.55 |
94.17 94.20 94.21 94.40 |
993.20 993.20 993.20 993.40 |
| 10 000×500 | SSVM FPSSVM TSSVM BSSVM1 |
10.46 9.64 9.84 11.41 |
89.04 89.18 89.19 190.22 |
89.80 89.80 89.80 89.80 |
| 1 000×1 000 | SSVM FPSSVM TSSVM BSSVM1 |
6.66 6.28 6.37 5.48 |
100.00 100.00 100.00 100.00 |
190.00 88.00 88.00 190.00 |
比较表中的计算时间可以看出BSSVM1模型的时间相比其他模型要高一点。但从表 1和表 2的训练样本正确率和测试样本正确率看出BSSVM1模型有最好的分类性能。因此我们可以得出结论,BSSVM1模型以牺牲少量的计算时间获得最优的分类性能。
4 结论综上所述,本文提出的一类一范式的BSSVM1模型能有效地解决二分类问题。本文采用四阶贝塞尔函数来测试BSSVM1模型的分类性能,无论是理论分析还是数值实验结果都表明,与以往提出的3种模型相比,BSSVM1模型的分类性能较好。
附录定理1的证明
证明 对于任意给定的x,k,B2(x,k)在插值节点x=± ,x=0满足下面的等式
,x=0满足下面的等式
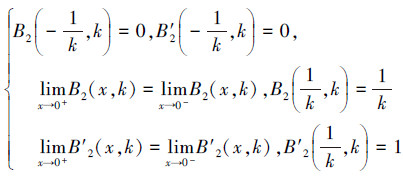
因此B2(x,k)关于x具有一阶光滑性。
B3(x,k)在插值节点x=± ,x=0满足下面的等式
,x=0满足下面的等式
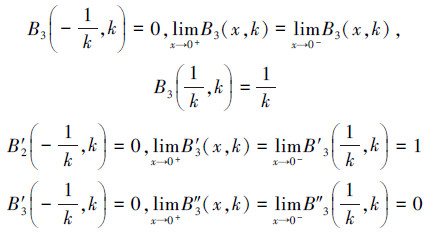
令Bp0,p1,…,pn-1表示由任意选择的点p0,p1,p2,…,pn-1决定的贝塞尔曲线。则
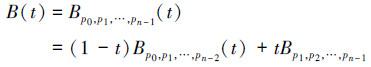
定理2的证明
证明
1. 分三步证明
1) 当x∈(-∞,- )∪(
)∪( ,+∞)时,结论显然成立
,+∞)时,结论显然成立
2) 当x∈(- ,0)时,x+=0并且Bn-1(x,k)单调递增,因此Bn-1(x,k)-x+≥0
,0)时,x+=0并且Bn-1(x,k)单调递增,因此Bn-1(x,k)-x+≥0
3) 当x∈(0, )∈(0,1)时,x+=x,因此
)∈(0,1)时,x+=x,因此
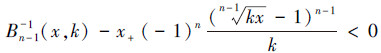
根据反函数的特性[9],我们可以证明Bn-1(x,k)-x+>0。
综合1)~(3),可知对任意x,k,有Bn-1(x,k)≥x。
2.以下分三步证明本定理之(2)
1) 当x∈(-∞,- )∪(
)∪( ,+∞)时,结论显然成立
,+∞)时,结论显然成立
2) 当x∈(- ,0)时,x+=0则
,0)时,x+=0则
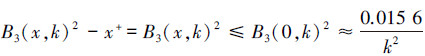
3) 当x∈(0, )时,x+≤
)时,x+≤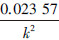
综合1)~3),可知对任意x,k,有B3(x,k)2-x+2≤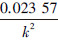 。同理,可以证明对任意x,k ,有B4(x,k)2-x+2≤
。同理,可以证明对任意x,k ,有B4(x,k)2-x+2≤ 。
。
| [1] | 张学工. 关于统计学习理论技持向量机[J]. 自动化学报, 2000(1):32-42 Zhang Xuegong. Introduction to Statistical Learning Theory and Support Vector Machine[J]. Acta Antomatica Sinica, 2000(1): 32-42 (in Chinese) |
| Cited By in Cnki (4633) | Click to display the text | |
| [2] | Lane, Maria, Rabelo, Baccarini. SVM Practical Industrial Application for Mechanical Faults Diagnostic[J]. Expert Systems with Applications, 2011, 38(6): 6980-6984 |
| Click to display the text | |
| [3] | Ingo Steinwart-Ardre. Support Vector Machines (Information Science and Statistics)[M]. Publisher: Springer, 2013 |
| [4] | Wang Yanhui, Zhang Chenchen, Luo Jun. Study on Information Fusion Algorithm and Application Based on Improved SVM[C]//IEEE Conference on Intelligent Transportation Systems, 2010: 1271-1276 |
| Click to display the text | |
| [5] | Lee Yuhjye, Mangasarian O L. SSVM: A Smooth Support Vector Machine for Classification[J]. Computational Optimization and Applications, 2001, 20(1): 5-22 |
| Click to display the text | |
| [6] | CHRISTOPHER J C BURGES. A Tutorial on Support Vector Machines for Pattern Recognition[J]. Data Mining and Knowledge Discovery, 1998, (2): 121-167 |
| Click to display the text | |
| [7] | Hardy G H. A Course of Pure Mathematics[M]. Beijing: Posts&Telecom Press, 2009 |
| [8] | 伍刚. 贝塞尔函数的计算机仿真研究[J]. Wu Gang. Journal of Industrial and Management Optimization (JIMO)[J]. 2013, 30(6): 105-107 |
| Cited By in Cnki | |
| [9] | Xiong Jinzhi, Hu Jinlian, Yuan Huaqiang, Hu Tianming, Li Guangming. Research on a New Class of Functions for Smoothing Support Vector Machines[J]. Acta Electronica Sinica, 2007, 35(2): 366-370 |
| Click to display the text | |
| [10] | Yuan Yubo, Huang Tingzhu. A Polynomial Smooth Support Vector Machine for Classification[J]. Advanced Data Mining and Applications, 2005, 3584(1): 157-164 |
| Click to display the text |