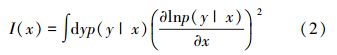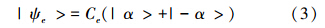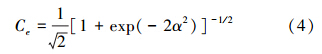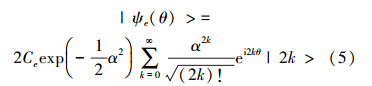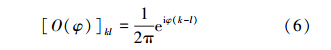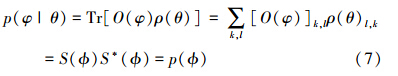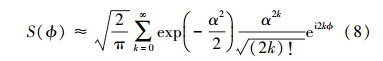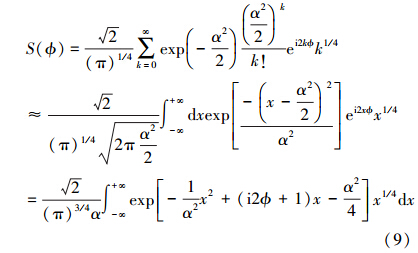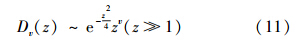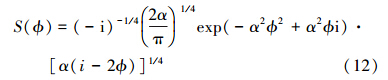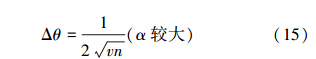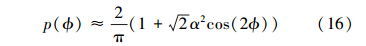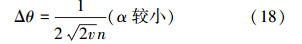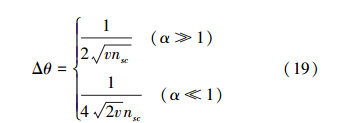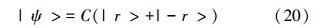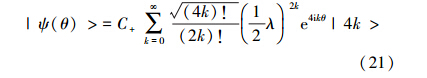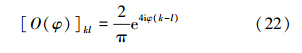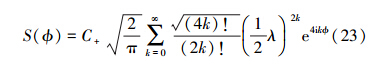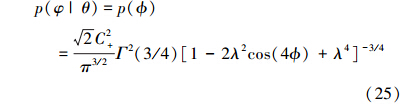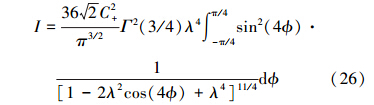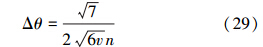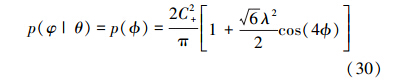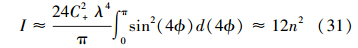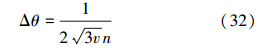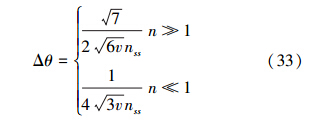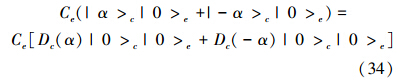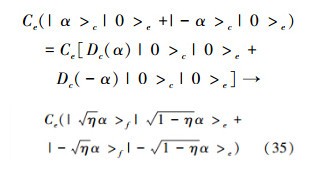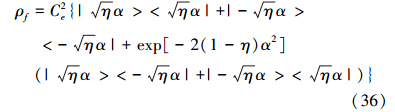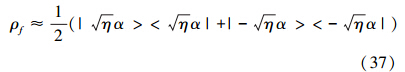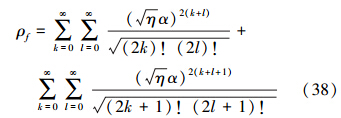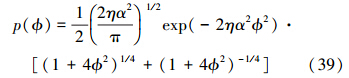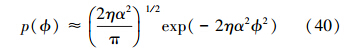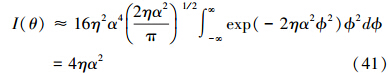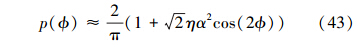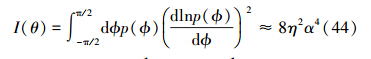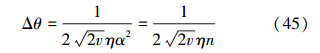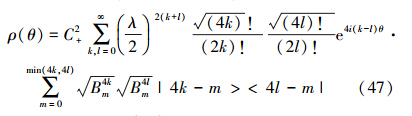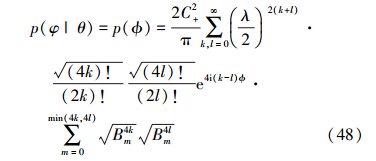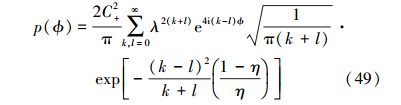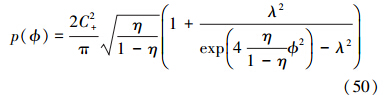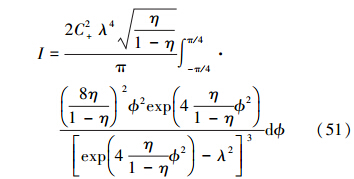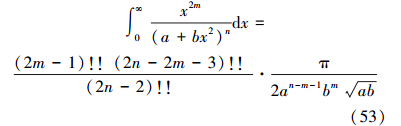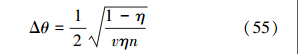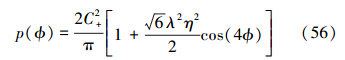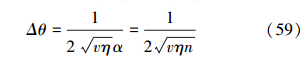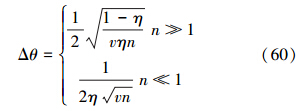引用本文
谢端, 苗瑞霞, 赵健. 叠加相干态与叠加压缩态的相位精度研究[J]. 西北工业大学学报, 2015, 33(2): 302-308
Xie Duan, Miao Ruixia, Zhao Jian. Phase Precision of Superposition of Coherent State and Superposition of Squeezed State[J]. Journal of Northwestern Polytechnical University, 2015, 33(2): 302-308.
叠加相干态与叠加压缩态的相位精度研究
谢端1, 苗瑞霞1, 赵健2    
1. 西安邮电大学电子工程学院, 陕西西安 710121;
2. 西北大学信息科学与技术学院, 陕西西安 710069
收稿日期: 2014-11-04
基金项目: 国家自然科学基金(51302215)与陕西省教育厅科学研究计划项目(14JK1682)资助
作者简介: 谢端(1979-),西安邮电大学讲师,主要从事量子信息及微电子研究。
摘要: 利用Cramér-Rao下界法计算了叠加相干态与叠加压缩态可以达到的最优相位精度。结果表明,平均粒子数较大时,叠加相干态的精度只能达到标准量子极限,而叠加压缩态精度更高,达到了海森伯格极限。应用损耗模型,分析了二态在有损信道中传输所受到的影响。研究显示2种量子态的精度都会有所下降。最后又加入了相干态与压缩态,将4种量子状态进行比较。比较结果显示,当各态平均粒子数较大时,压缩态与叠加压缩态精度较高。当平均粒子数较小时,随着损耗的增加,叠加压缩态对外界环境的影响显得很敏感,其精度衰减得更快些。
关键词: 相位精度     叠加相干态     叠加压缩态     有损信道    

由于利用量子测量方法,可以得到很高的参数精度。近些年来,人们利用该方法在原子光谱分析[1]、磁力测量[2]、光学干涉测量[3]等领域进行了研究和实验,并取得一定成果。

理论证明,对经典量子态的参数(如相位)进行测量,其精度正比于 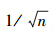,也即达到标准量子极限。而利用一些非经典的量子态,其测量精度正比于1／n,可以达到海森伯格极限。这里n指的是量子态中所包含的平均粒子数。

纠缠态和压缩态是2种重要的非经典量子态,一些研究已证明利用这2种量子态可以将测量精度提高到海森伯格极限[4]。而非经典的量子态很多,其它类型的量子态是否也可以使测量精度达到海森伯格极限。为此,本文选取了2种典型的非经典量子态,叠加相干态和叠加压缩态,研究它们用于测量所可能达到的最优精度。一般的,若有2种状态|ψ+>和|ψ->,其宏观上可区分,它们叠加后形式为|ψ>∝|ψ+>+|ψ->,叠加态|ψ>也称为薛定谔猫态。NOON态是一种纠缠态,它同时也是一种薛定谔猫态。薛定谔猫态在量子测量甚至在整个量子力学领域,都有着重要的地位和作用。近年来,猫态吸引了很多学者目光,尤其是叠加相干态和叠加压缩态[5, 6]。Ourjoumtsev等人报道其已在实验室成功制备了叠加相干态和叠加压缩态[7, 8]。

实际应用中,量子态在传输过程中不可避免地会与信道发生作用,产生损耗。虽然先期有关损耗对精度影响的研究文献较少,但已有的少许研究显示,一些量子态非常易受有损信道的影响,其精度会大幅下降[9, 10, 11]。举例来说,若NOON态在传输中损失一个粒子,最终会变成(N-1,0＞＜N-1,0+0,N-1><0,N-1)／2,也即从纯态变为混合态,这会造成较大的测量误差。因此本文还将研究在量子光学通信系统中,光子损耗对测量精度的影响。我们会建立一个有损信道模型,分析常见量子态在损耗情况下可能达到的相位精度。该损耗模型,主要基于一个反射系数可调的分束器,其反射系数的大小与损耗程度的高低相应。

1 无损耗情况下叠加相干态与叠加压缩态的相位精度分析 1.1 Cramér-Rao下界法

本文需要利用Cramér-Rao下界法确定量子态精度。量子测量学主要任务是把隐含在量子态ρx 中的某一参量x提取出来。在量子态测量中,这一参量可以是相位。量子测量又可以分为2步:对某一量子系统S进行测量,得到数据结果;再分析测量结果以便提取出x的值。对量子态的测量可以采用POVM测量。POVM测量需有一个正定算符集合｛Ex｝,并且算符之和满足 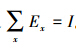。如果对n个量子态ρx进行测量,得到结果y的条件几率为pn(y|x)=Tr(Exρxn)。对结果y进行数据分析可以得到估计值z。我们希望估计值z能够非常接近真实值x。然而,实际估计值与真实值之间会有一定的误差。假使测量是渐进无偏的,该误差可表示为

式中，右边的值就是Cramér-Rao下界[12]。要使(1)式成立,必须保证测量样本v→∞[13]。另外要指出,(1)式中,I(x)就是Fisher信息量。它可以表示为

可见要得到误差值(精度),计算出Fisher信息量是关键。

1.2 叠加相干态精度估计

叠加相干态如下式所示

式中，Ce是归一化常数

简单起见,取α为实数。由于时间演化,|ψe(θ)>可以表示为

通过对此演化态的POVM测量,就可确定相位θ值。我们要选择一个正定算符集合｛Eχ｝,并使它满足 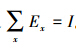。在此,选择Holevo正则相位测量元[14],它可以表示为

式中,[O(φ)]kl= < k|O(φ)|l>,可以验证其满足完备性∫O(φ)dφ=I。

对于叠加相干态,结果为φ的条件几率为

式中,ϕ=φ-θ。要得到条件几率,首先要求得S(ϕ)的值。先考虑α较大的情况,简单计算可以得到

通过斯特令公式,可以近似得到 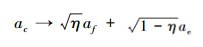(kπ)-1／4。这样(8)式近似为

在(9)式中,我们用正态分布近似了泊松分布,再利用积分公式[15]

以及抛物柱面方程的渐进特性

可以得到

因此

将公式(13)代入(2)式,可以得到

所以最优的精度为

当α较小时(α«1),由(7)式计算p(ϕ)时,只精确到α的一次项,有

下面将精度的表达式转化为其与平均粒子数nsc的关系。当α较大时,叠加压缩态的平均粒子数为nsc=α2=n;而当α较小时,平均粒子数为nsc=0.5α2=0.5n。用平均粒子数来表示精度,可以得到

当平均粒子数较大时,叠加相干态的精度达到标准量子极限。

1.3 叠加压缩态精度估计

如果将2个反方向的真空压缩态叠加,就可以得到叠加压缩态

归一化因子 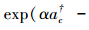。由于时间演化,将会产生一个相移θ。演化后的状态可以表示为

(21)式中 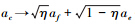。我们要将|ψ(θ)>中所含的相位信息提取出来。对于叠加压缩态,其Holevo正则测量元为

它满足完备性∫O(φ)dφ=I。可以求得

首先,考虑大的压缩极限(n>>1 or λ→1)。应用斯特令公式,可以得到

由此,可以得到

将(25)式代入(2)式,可以得到费舍尔信息量

由于λ→1,在 ϕ→0附近积分函数对积分的贡献较大。可以将积分限从π／4拓展到∞,这样就有

最终可以得到

所以最优的精度为

相反情况下,如果处于小压缩极限,有n « 1。 在此极限下 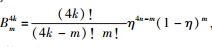,在计算条件几率时,只需展开到λ2项。这样近似的几率为

因此

当λ→1,也即n较大时,叠加压缩态的平均粒子数为nss=n;小压缩极限下,nss=0.5n。综上分析,叠加压缩态的精度值为

2 有损信道对量子态的精度影响分析 2.1 叠加相干态的损耗分析

量子光学已在近些年中快速发展,其传播信道可以是光纤或是自由空间。但无论何种类型的信道,都会有光子损耗。本节我们搭建一个简单的光子损耗模型,以此来研究叠加相干态的精度受损耗的影响。

在图 1中,初态会经过一个延迟器与一个分束器到达检测端。量子幺正操作或是其随时间演化可以看作是一个相移θ。光子的损耗可由一个假想的分束器来描述,该分束器透射系数可调。假设其透射系数为η,则c端口湮灭算符为 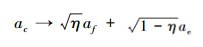[16]。其中ai(i=c,f,e)分别为每个端口的湮灭算符。例如一个叠加相干态与环境相耦合,其可以表示为

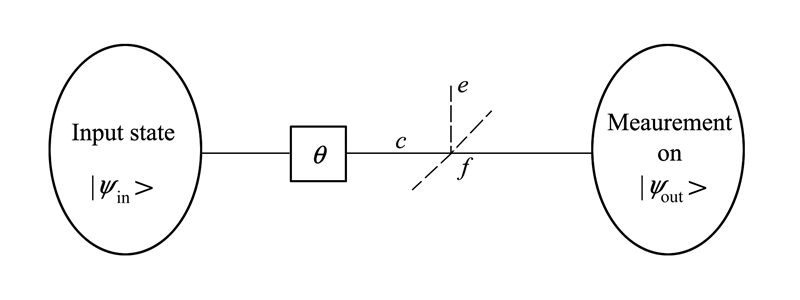图 1 光子损耗模型
图选项

式中,Dc(α)为位移算符,其值为 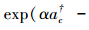α*ac)。将 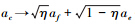,可以得到

对环境e取偏迹得

(36)式可以看作是4项相加。当α较大时,可以将后2项忽略,则有

将该状态展开成Fock态的形式

可以求得

因为ϕ通常是一个很小的值,所以

代入到(2)式中,得

当α较小时,对(38)式只计算到α2项,有

用平均粒子数来表示精度,可以得到

2.2 叠加压缩态的损耗分析

与上面叠加相干态损耗分析类似。当叠加压缩态经过分束器,对环境取偏迹,得到

式中,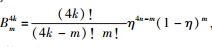 ,m为损失的光子数。由于p(φ|θ)=Tr[O(φ)ρ(θ)],易得到

用均值为4k(1-η)的正态分布近似二项式分布Bm4k,再应用斯特令近似 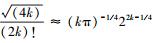,可得

令s=k+l,u=k-l。可简化得到

将(50)式代入(2)式,得

大压缩极限下,λ→1,此时被积函数在较小时对积分贡献较大。在此情况下,有近似λ2≈1-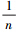 和 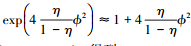。将积分限扩展到(-∞,+∞),得到

利用积分公式[17]

最终得到

所以,最优相位为

小压缩极限下,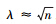 ,对(47)式只取到λ2项,有

这样,可得到

综上分析,叠加压缩态的精度值为

3 结果分析与比较

在这一节中,我们将对比相干态,压缩态及它们的叠加态的精度。省略推导过程,受损耗影响,相干态与压缩态精度分别如(59)式和(60)式所示

图 2显示了当平均粒子数较大时,4种量子态的精度随η值的变化。我们取平均粒子数为100的情况进行比较。相干态和压缩态分别与其叠加形式的精度相同,它们随着η值的减小(也即有损程度的增加),精度不断下降。由于当0 < η < 1时,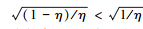 ,故而压缩态与叠加压缩态精度较高。图 2中还有2条水平虚线,它们分别表示在平均粒子数为100时,相干态与压缩态通过理想信道所能达到的精度。对比发现,随着η值的减小,2条精度变化曲线与理想信道的精度偏离越来越大。由于当η=0.5时, 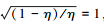,此时压缩态与叠加压缩态精度从海森伯格极限降低到标准量子极限。当η值进一步减小时,它们的精度继续降低,甚至会低于理想情况下相干态所达到的标准量子极限。

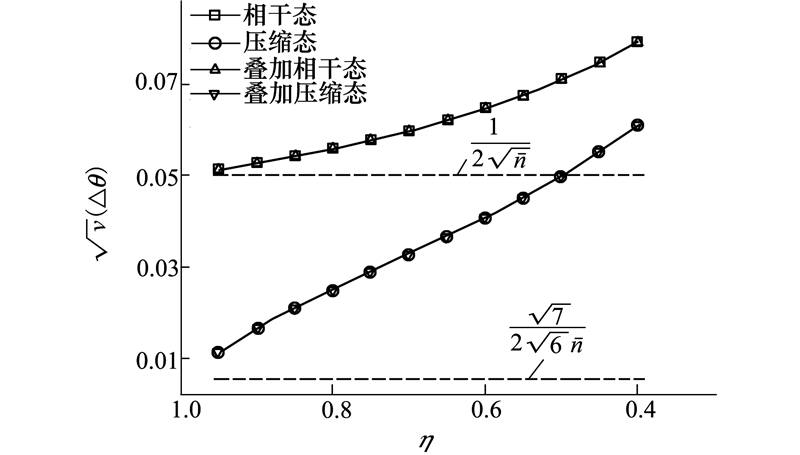图 2 有损信道对各量子态精度影响(平均粒子数=100)
图选项

图 3又对比了在另一种极限下(也即平均粒子数较小时),各态精度随损耗的变化,此时各态的精度皆不相同。当 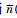(平均粒子数)和η均处于0到1区间范围内时,有 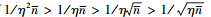,故而叠加压缩态的精度随损耗的增加降低的最快,其次是叠加相干态,再次是压缩态,最后是相干态。在平均粒子数较小时,叠加压缩态和叠加相干态对损耗影响变得很敏感,它们的精度较低。相较于它们,相干态在此时具有一定的优势,它的精度也高于其他三者。损耗情况下,经典的相干态在平均粒子数较小时,比一些非经典量子态具有一定的优势。

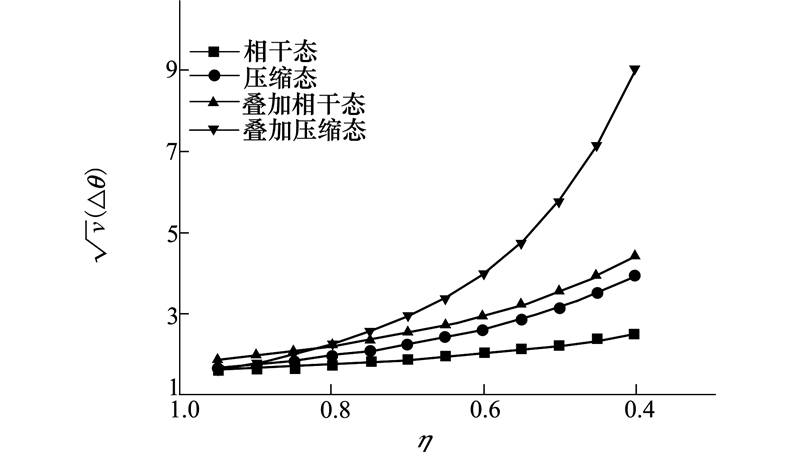图 3 有损信道对各量子态精度影响(平均粒子数=0.1)
图选项
4 结 论

本文研究了无损与有损情况下,叠加相干态与叠加压缩态的最优相位精度。利用分束器建立了一个信道损耗模型,根据此模型计算了2种量子态的精度。研究显示各态受损耗的影响,精度均有所下降。当平均粒子数较大或较小时,其精度变化有所不同:

1) 当各态平均粒子数较大时,压缩态和相干态分别与其叠加形式精度相同。在一定损耗范围内,压缩态与叠加压缩态精度较高。

2) 当各态平均粒子数较小时,随着损耗的增加,叠加压缩态对外界环境的影响显得很敏感,其精度衰减的更快些。此时经典的相干态精度最高。

参考文献
[1] Sewell R J, Koschorreck M, Napolitano M, et al. Magnetic Sensitivity beyond the Projection Noise Limit by Spin Squeezing[J]. Phys Rev Lett, 2012, 109:253605
Click to display the text
[2] Higgins1 B L, Berry D W, Bartlett S D, et al. Demonstrating Heisenberg-Limited Unambiguous Phase Estimation without Adaptive Measurements[J]. New J Phys, 2009, 11:073023
Click to display the text
[3] Emilio Bagan, Alex Monras, Ramon Munoz-Tapia, et al. Phase Variance of Squeezed Vacuum States[J]. Phys Rev A, 2008, 78:043829
Click to display the text
[4] Lee Changwoo, Jeong H. Effects of Squeezing on Quantum Nonlocality of Superpositions of Coherent States[J]. Phys Rev A, 2009,80:052105
Click to display the text
[5] Stobińska M, Jeong H, Ralph T C. Violation of Bell's Inequality Using Classical Measurements and Nonlinear Local Operations[J]. Phys Rev A, 2007, 75:052105
Click to display the text
[6] Ourjoumtsev Alexei, Tualle-Brouri Rosa, Laurat Julien, et al. Generating Optical Schr dinger Kittens for Quantum Information Processing[J]. Science, 2006,312(5770):83-86
Click to display the text
[7] Ourjoumtsev Alexei, Jeong Hyunseok, Tualle-Brouri Rosa, et al. Generation of Optical Schr dinger Cats from Photon Number States[J]. Nature, 2007, 448:784-786
Click to display the text
[8] Kołodyński J, Demkowicz-Dobrzański R. Phase Estimation without a Priori Phase Knowledge in the Presence of Loss[J]. Phys Rev A, 2010, 82:053804
Click to display the text
[9] Knysh S, Smelyanskiy V N, Durkin G A. Scaling Laws for Precision in Quantum Interferometry and the Bifurcation Landscape of the Optimal State[J]. Phys Rev A, 2011, 83:021804
Click to display the text
[10] Cooper J J, Dunningham J A. Towards Improved Interferometric Sensitivities in the Presence of Loss[J]. New Journal of Physics, 2011, 13(11):115003
Click to display the text
[11] Helstrom C W. Quantum Detection and Estimation Theory[M]. Academic Press, New York, 1976
[12] Vittorio Giovannetti, Seth Lloyd, Lorenzo Maccone. Advances in Quantum Metrology[J]. Nature Photonics, 2011, 5:222-229
Click to display the text
[13] Holevo A S. Covariant Measurements and Imprimitivity Systems[J]. Lect Notes Maths, 1984, 1055:153-172
Click to display the text
[14] Gradshteyn I S, Ryzhik I M. Table of Integrals, Series, and Products[M]. Massachusetts Academic Press, 2007
[15] Animesh Datta, Lijian Zhang, Nicholas Thomas-Peter, et al. Quantum Metrology with Imperfect States and Detectors[J]. Phys Rev A, 2011, 83:063836
Click to display the text
[16] 金玉明,薛兴恒,顾新身,等.实用积分表[M].合肥:中国科技大学出版社,2006 Jing Y M, Xue X H, Gu X S, et al. The Utility Table of Integrals[M]. Hefei:University of Science and Technology of China Press, 2006(in Chinese)
Phase Precision of Superposition of Coherent State and Superposition of Squeezed State
Xie Duan1, Miao Ruixia1, Zhao Jian2     
1. School of Electronic Engineering, Xi'an University of Posts and Telecommunications, Xi'an 710121, China;
2. School of Information Science and Technology, Northwest University, Xi'an 710069, China
Abstract: This paper studies optimal phase precision of superposition of coherent state and superposition of squeezed state using Cramér-Rao bound approach. The results show that precision of superposition of coherent state only achieves the standard quantum limit and precision of superposition of squeezed state achieves Heisenberg limit. Using a dissipation model, we find accuracies of two quantum states decrease with increasing loss degree(η).We also introduce coherent state and squeezed state and compare accuracies of four quantum states. When mean particle number is bigger, phase precisions of squeezed state and superposition of squeezed state are higher. When mean particle number is smaller,with the increasing loss of particle, phase precision of superposition of squeezed state decreases much faster as it is more susceptible to the environment.
Key words: phase precision     superposition of coherent state     superposition of squeezed state     dissipative channel     Cramer-Rao bounds     errors     estimation     normal distribution     optimization     photons     Poisson distribution     probability     Cramer-Rao lower bound method     dissipation analysis of superposition of squeezed states     dissipation channel     effect of dissipation channel on precision of each quantum state     mean particles number     phase precision     photon dissipation model     precision estimation of superposition of coherent states     precision estimation of superposition of squeezed states    
西北工业大学主办。
0

文章信息

谢端, 苗瑞霞, 赵健
Xie Duan, Miao Ruixia, Zhao Jian
叠加相干态与叠加压缩态的相位精度研究
Phase Precision of Superposition of Coherent State and Superposition of Squeezed State
西北工业大学学报, 2015, 33(2): 302-308
Journal of Northwestern Polytechnical University, 2015, 33(2): 302-308.

文章历史

收稿日期: 2014-11-04

相关文章

工作空间